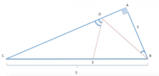
[math]ABC[/math]
si ha:
[math] AB = a , BC = 2a , hat{ABC} = 2/3 π = 120° [/math]
Condurre dal vertice
[math]C[/math]
la perpendicolare al lato [math]CB[/math]
fino ad incontrare in [math]M[/math]
il lato [math]AB[/math]
e calcolare la lunghezze dei segmenti [math]AM[/math]
, [math]BM[/math]
e [math]CM[/math]
.

Svolgimento
Con il teorema del coseno, possiamo determinare la lunghezza del segmento[math]AB[/math]
:
[math]AB^2 = AC^2 + BC^2 - 2 \cdot AC \cdot CB \cdot \\cos(hat{ACB}) = [/math]
[math] a^2 + (2a)^2 - 2 \cdot a \cdot 2a \cdot \\cos(120°) = a^2 + 4a^2 - 4a^2 \cdot (-1/2) = 5a^2 + 2a^2 = 7a^2 [/math]
[math] AB = \sqrt{7a^2} = \sqrt7 a [/math]
applichiamo il teorema dei seni al triangolo
[math]ABC[/math]
e troviamo il seno dell'angolo [math]hat{ABC}[/math]
:
[math] frac(AB)(\\sin (hat{ACB})) = frac(AC)(\\sin (hat{ABC})) \to \\sin(hat{ABC}) = frac(\\sin (hat{ACB}) \cdot AC)(AB) = [/math]
[math]frac(a \cdot frac(\sqrt3){2})(\sqrt7 a) = frac(\sqrt3){2} a \cdot frac(1)(\sqrt7 a) = frac(\sqrt3)(2 \sqrt7) = frac(\sqrt(21))(14)[/math]
[math] \\cos (hat{ABC}) = \sqrt{1 - \\sin ^2 (hat{ABC})} = \sqrt(1 - frac(21)(196)) = \sqrt(frac(175)(196)) = frac(5 \sqrt7)(14) [/math]
Consideriamo il triangolo rettangolo
[math]CMB[/math]
. Determiniamo la misura del lato [math]MB[/math]
tramite il primo teorema della trigonometria:
[math] MB = frac(CB)(\\cos(hat{ABC})) = frac(2a)(frac(5\sqrt7){14}) = 2a \cdot frac{14}(5\sqrt7) = frac(28)(5 \sqrt7) a[/math]
Calcoliamo la misura del cateto
[math]CM[/math]
tramite il teorema di Pitagora:
[math]CM = \sqrt{MB^2 - CB^2} = \sqrt((frac(28)(5 \sqrt7) a)^2 - (2a)^2) = [/math]
[math] \sqrt{frac(784)(175) a^2 - 4a^2} = \sqrt(frac(784 - 700)(175) a^2) = [/math]
[math]\sqrt{frac(84)(175)} a = frac(2 \sqrt3)(5) a [/math]
Troviamo ora il segmento AM per differenza:
[math]AM = AB - BM = \sqrt7 a - frac{4 \sqrt7}(5) a = [/math]
[math] frac(5 \sqrt7 a - 4 \sqrt7 a){5} = frac(\sqrt7){5} a [/math]