[math]O[/math]
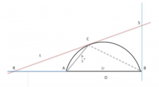
e diametro [math] AB = 10 [/math]
, condurre per il punto [math]C[/math]
, posto sul prolungamento di [math]AB[/math]
dalla parte di [math]A[/math]
, la semiretta tangente in [math]M[/math]
alla semicirconferenza. Sapendo che:
[math] tg(hat{MCO}) = tg(alpha) = 3/4 [/math]
determinare:
- Le misure di [math]OC[/math]e di[math]CM[/math];
- La misura della corda [math]MB[/math];
- La misura di [math]AH[/math], essendo[math]H[/math]il piede della perpendicolare condotta da[math]M[/math]ad[math]AB[/math].

Svolgimento (1)
Consideriamo il triangolo[math]CMO[/math]
: esso è rettangolo, poiché la tangente nel punto [math]M[/math]
forma con il raggio un angolo retto.Poiché il problema fornisce il valore della tangente di uno dei suoi angoli, possiamo applicare il secondo teorema della trigonometria per trovare il valore del lato
[math]MC[/math]
:
[math] MC = MO \cdot tg(hat{MOC}) = MO \cdot cotg(alpha) [/math]
[math] MC = MO \cdot cotg(alpha) = MO \cdot frac(1)(tg(alpha)) = 5 \cdot frac(1)(3/4) = 5 \cdot 4/3 = (20)/3 [/math]
Possiamo trovare la misura di
[math]CO[/math]
sfruttando il teorema di Pitagora:
[math] CO = \sqrt{MC^2 + MO^2} = \sqrt((frac(20)(3))^2 + (5)^2) = \sqrt(frac(400)(9) + 25) = [/math]
[math]\sqrt{frac(400 + 225)(9)} = \sqrt(frac(625)(9)) = frac(25)(3) [/math]
Svolgimento (2)
Per trovare la misura della corda[math]MB[/math]
, consideriamo il triangolo [math]CMB[/math]
. Determiniamo il seno dell'angolo [math]alpha[/math]
:
[math] \\sin (alpha) = frac(tg(alpha))(\sqrt{1 + tg^2(alpha)}) = frac(3/4)(\sqrt(1 + (3/4)^2)) = [/math]
[math] frac(3/4)(\sqrt{1 + 9/(16)}) = frac(3/4)(\sqrt(frac(25)(16))) = frac(3/4)(5/4) =3/4 \cdot 4/5 = 3/5 [/math]
Possiamo trovare la misura di
[math]CB[/math]
:
[math] CB = CO + OB = (25)/3 + 5 = (40)/3 [/math]
Applichiamo ora il teorema dei seni al triangolo
[math]COM[/math]
:
[math] frac(MO)(\\sin (alpha)) = frac(CM)(\\sin(hat{COM})) \to \\sin(hat{COM}) = frac(\\sin (alpha) \cdot CM)(MO) = [/math]
[math] frac((20)/3 \cdot 3/5)(5) = 4/5 [/math]
Determiniamo anche il coseno dell'angolo:
[math] \\cos (hat{COM}) = \sqrt{1 - \\sin ^2 (hat{COM})} = \sqrt(1 - (4/5)^2) = \sqrt(1 - frac(16)(25)) = [/math]
[math] \sqrt{frac(9)(25)} = 3/5 [/math]
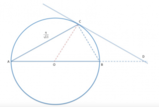
Notiamo che l'angolo
[math]hat{COM}[/math]
(angolo al centro) è doppio dell'angolo [math]hat{OBM}[/math]
(alla circonferenza), poiché essi insistono sulla stessa corda, quindi:
[math] hat{MBO} = frac(hat{COM})(2) [/math]
[math] \\sin (hat{MBO}) = \\sin (frac(hat{COM})(2)) [/math]
Applichiamo le formule di bisezione:
[math] \\sin (frac(hat{COM})(2)) = \sqrt{frac(1 - \\cos(hat{COM}))(2)} = [/math]
[math] \sqrt{frac(1 - 3/5)(2)} = \sqrt(2/5 \cdot 1/2) = frac(1)(\sqrt5) [/math]
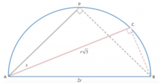
Applichiamo ora il teorema dei seni al triangolo
[math]CMB[/math]
per determinare la lunghezza del lato [math]MB[/math]
:
[math] frac(CM)(\\sin (hat{MBO})) = frac(MB)(\\sin(alpha)) \to MB = frac(\\sin(alpha) \cdot CM)(\\sin (hat{MBO})) [/math]
[math] MB = frac(3/5 \cdot (20)/3)(frac(1)(\sqrt5)) = 4 \cdot \sqrt5 = 4\sqrt5 [/math]
Svolgimento (3)
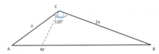
Per trovare la misura di[math]AH[/math]
, consideriamo il triangolo rettangolo [math]MHB[/math]
e determiniamo la misura di [math]MH[/math]
:
[math] MH = MB \cdot \\sin (hat{MBO}) = 4\sqrt5 \cdot frac{1}(\sqrt5) = 4 [/math]
Troviamo quindi
[math]HB[/math]
con il teorema di Pitagora:
[math] HB = \sqrt{MB^2 - HM^2} = \sqrt((4\sqrt5)^2 - 4^2) = \sqrt(80-16) = \sqrt(64) = 8 [/math]
Possiamo trovare il segmento
[math]AH[/math]
per differenza:
[math]AH = AB - HB = 10 - 8 = 2 [/math]