Coordinate sferiche e cilindriche nello spazio

Posizione e sistema di riferimento

Per ulteriori approfondimenti sui sistemi di riferimento vedi qua

Coordinate sferiche nello spazio

Le coordinate sferiche sono sempre tre e sono indicate con lettere dell'alfabeto greco. Una coordinata esprime una misura di lunghezza nella unità prefissata, le altre due sono misure angolari:

• [math]\rho[/math]
• [math]\theta[/math]
• [math]\phi[/math]

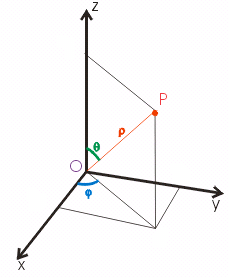
• [math]\rho[/math]
  =OP: è una lunghezza, misura della distanza del punto P dall’origine O;
• [math]\theta[/math]
  : è l’angolo formato tra la congiungente OP e l’asse z, detto anche colatitudine o angolo polare
• [math]\phi[/math]
  : è l’angolo formato tra l'asse x e la proiezione del segmento OP sul piano xy

Come passare dalle coordinate sferiche alle coordinate cartesiane

• La componente x del punto P è data dal prodotto della proiezione di OP sul piano xy per il coseno dell’angolo
  [math]\phi[/math]
• La componente y del punto P è data dal prodotto della proiezione di OP sul piano xy moltiplicata per il seno dell’angolo
  [math]\phi[/math]
• La componente z del punto P è data dal prodotto della lunghezza di OP per il coseno di
  [math]\theta[/math]
• La proiezione di OP sul piano xy è in funzione dell’angolo theta

Con le seguenti condizioni sui valori possibili:

Invece per passare dalle coordinate cartesiane

Coordinate cilindriche

Detta

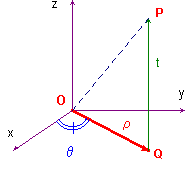
• Il parametro
  [math]z[/math]
  indica la lunghezza di
  [math]PQ[/math]
  , ovvero la quota del punto P.
• Il parametro
  [math]\rho[/math]
  indica la lunghezza di
  [math]OQ[/math]
  , la distanza tra l’origine e la proiezione del punto P sul piano xy.
• Il parametro
  [math]\theta[/math]
  indica l'angolo fra il semiasse positivo delle
  [math]x[/math]
  e
  [math]OQ[/math]
  .


Sempre utilizzando le relazioni trigonometriche tra i lati e li angoli di un triangolo, andiamo a scrivere le equazioni della trasformazione per esprimere le coordinate cartesiane (x,y,z) in funzione di quelle cilindriche:

[math]\begin{cases} x =\rho \cdot cos(\theta) \\ y =\rho \cdot sin (\theta) \\ z = z \end{cases} [/math]

Con le seguenti condizioni sui valori possibili:

[math]\rho \in [0, +\infty),\\ \theta \in [0, 2\pi),\\ z \in (-\infty, +\infty)[/math]

Queste coordinate possono essere viste anche come coordinate polari piane. Inoltre l’asse di simmetria coincide con l’asse zeta. In caso di necessità è possibile traslare l’asse e quindi considerare un sistema di coordinate cilindriche con asse di simmetria traslato e parallelo all’asse z. Detto r questo asse, è comunque una retta dello spazio e la sua equazione possiamo scriverla in forma cartesiana:

[math]r: \begin{cases} x=x_0 \\ y=y_0 \end{cases} [/math]

Applicando la traslazione alle coordinate cilindriche abbiamo:

[math]\begin{cases} x =x_0+\rho \cdot cos(\theta) \\ y =y_0+\rho \cdot sin (\theta) \\ z = z \end{cases} [/math]

Equazioni delle coordinate cilindriche in funzione delle coordinate cartesiane

Delle tre coordinate la quota resta invariata, perciò è sempre
[math]z[/math]
.
La coordinata
[math]\rho[/math]
, è la misura della distanza OQ:
[math]\rho=\overrightarrow{OQ}=\sqrt{x^2+y^2}[/math]

Il valore di

[math]\theta[/math]
dipende dalla posizione de punto. Per calcolarne il valore scriviamo le su funzioni seno e coseno:
[math]cos(\theta)=\frac{x}{\sqrt{x^2+y^2}}[/math]
[math]sin(\theta)=\frac{y}{\sqrt{x^2+y^2}}[/math]

con:

[math]\theta \in [0, 2\pi)[/math]

Per risalire al valore di

[math]\theta[/math]
, ricorriamo alle funzioni goniometriche inverse:
[math]\theta)=\arccos\big(\frac{x}{\sqrt{x^2+y^2}}\big)[/math]
[math]\theta=\arcsin \big(\frac{x}{\sqrt{x^2+y^2}}\big)[/math]

Per ulteriori approfondimenti sulle funzioni arcoseno e arcocoseno vedi qua

Quando utilizzare le coordinate cilindriche

Nella risoluzione degli integrali tripli risulta comodo utilizzare questo sistema di coordinate, la presenza della somma
[math]x^2+y^2[/math]
indica che vi è una simmetria assiale.
Usiamo queste coordinate se:

• la funzione da integrare dipende dalla somma dei quadrati di x ed y, cioè da:
  [math]x^2+y^2[/math]
• il dominio di integrazione è un cilindro, oppure una parte di esso
Vediamo qualche esempio
Supponiamo di avere un insieme così definito:
[math]A=\big\{(x,y,z)\in \Re^3: x^2+y^2\leq 1, -1\leq z\leq 1\big\}[/math]

L’insieme dei punti dello spazio appartenenti ad A, definiscono un cilindro di raggio unitario ed altezza pari a 2.
Infatti la quota compresa tra -1 ed 1 ci fa capire che il nostro cilindro ha altezza pari a 2.
Usiamo le equazioni:

[math]\begin{cases} x =\rho \cdot cos(\theta) \\ y =\rho \cdot sin (\theta) \\ z = z \end{cases} [/math]

elevando al quadrate le prime due:

[math]\begin{cases} x^2 =\rho^2 \cdot cos^2(\theta) \\ y^2 =\rho^2 \cdot sin^2 (\theta) \end{cases} [/math]

otteniamo:

[math]x^2+y^2\leq 1 \to =\rho^2 \cdot cos^2(\theta)+ =\rho^2 \cdot sin^2(\theta)\leq 1[/math]

per la prima relazione fondamentale della goniometria:

[math]\rho^2 \leq 1[/math]

che per

[math]\rho\geq 0[/math]
, porta alla soluzione:
[math]\rho \in [0, 1][/math]
.

L’angolo

[math]\theta[/math]
varia nel suo dominio naturale:
[math]\theta \in [0, 2\pi)[/math]
La condizione su z è fissata:
[math]-1\leq z\leq 1[/math]
.

A questo punto riscriviamo l’insieme A con le coordinate cilindriche:

[math]A=\big\{(\rho,\theta,z):0\leq \rho \leq 1,\ \ \theta \in [0, 2\pi),z \in [-1,1]\big\}[/math]