Determinante di una matrice
Il determinante è definito solo per matrici quadrate, cioè per matrici che hanno lo stesso numero di righe e colonne. Il calcolo del determinante sfrutta un metodo ricorsivo: si definisce il determinante per matrici[math]1\times 1[/math]
(cioè costanti) e [math]2 \times 2[/math]
, fatto questo si definisce il determinante di una matrice [math]n \times n[/math]
come il determinante di una o più matrici [math](n-1)\times(n-1)[/math]
, e si applica tale regola fino a ricondursi a matrici di ordine [math]2 \times 2[/math]
o a costanti.
Matrici [math]1 \times 1[/math]
Il determinante di una matrice del primo ordine cioè di una costante, coincide con la costante stessa:
[math]|c|= c,\\ \forall c \in \mathbb{\Re}[/math]
Matrici [math]2 \times 2[/math]
Il determinante di una matrice del secondo ordine del tipo:
[math]A=\begin{bmatrix} a & b \\ c & d \end{bmatrix}[/math]
è dato dalla differenza tra il prodotto degli elementi sulla diagonale principale “ad” e quello degli elementi sulla diagonale secondaria “bc”:
[math]\det(A)=|A|=ad-bc[/math]
Matrici [math]n \times n[/math]
Diamo la formula generale per una matrice quadrata di ordine
[math]n \wedge n>2[/math]
, ma per fare questo occorrono due definizioni importanti alla comprensione dei successivi passaggi, quella del minore complementare e quella del complemento algebrico.
Definizione di minore complementare
Data una matrice
[math]A[/math]
quadrata di ordine [math]n[/math]
, si definisce minore complementare dell'elemento di posto [math]ij[/math]
, e si indica con [math]M_{ij}[/math]
, come il determinante della matrice che si ottiene cancellando l'[math]i[/math]
-esima riga e la [math]j[/math]
-esima colonna.
Definizione di complemento algebrico
Data una matrice
[math]A[/math]
di ordine [math]n[/math]
, si definisce complemento algebrico dell'elemento di posto [math]ij[/math]
, e si indica con [math]C_{ij}[/math]
, il prodotto:
[math]C_{ij}=(-1)^{i+j} \cdot M_{ij}[/math]
dove
[math]M_{ij}[/math]
è il minore complementare ottenuto come alla definizione precedente.Diamo ora la definizione generale valida per ogni ordine
[math]n>2[/math]
:Il determinante di una matrice quadrata di ordine
[math]n[/math]
si ottiene come somma dei prodotti fra gli elementi di una qualunque riga, o colonna, per i rispettivi complementi algebrici.Sviluppando rispetto alla riga
[math]i[/math]
-esima il determinante vale:
[math]det(A) = a_{i1}C_{i1}+a_{i2}C_{i2}+ \ldots +a_{i n}C_{i n}[/math]
Sviluppando rispetto alla colonna
[math]j[/math]
-esima il determinante vale:
[math]det(A) = a_{1j}C_{1j}+a_{2j}C_{2j}+ \ldots +a_{nj}C_{nj}[/math]
In entrambi i casi con
[math]a_{ij}[/math]
si intende l'elemento di posto [math]ij[/math]
della matrice [math]A[/math]
. Per ulteriori approfondimenti sulle matrici vedi qua
Esempio di calcolo del determinante di una matrice [math]3\times 3[/math]
Il determinante non dipende dalla particolare riga o colonna che si sceglie per lo sviluppo. Calcoliamo il determinante di una matrice del terzo ordine, così vediamo come applicare la definizione.
[math]A=\begin{pmatrix}5 & 6 & 3 \\ 1 & 2 &7 \\ 3 & 4 & 5 \end{pmatrix}[/math]
Sviluppiamo lungo la prima colonna e abbiamo:
[math]|A| = 5 C_{11} + 1 C_{21} +3 C_{31}[/math]
In cui:
[math]C_{11}=\begin{vmatrix}2 & 7 \\ 4 & 5 \end{vmatrix}=10-28=-18[/math]
[math]C_{21}=-\begin{vmatrix}6 & 3 \\ 4 & 5 \end{vmatrix}=30-12=18[/math]
[math]C_{31}=\begin{vmatrix}6 & 3 \\ 2 & 7 \end{vmatrix}=42-6=36[/math]
Otteniamo quindi:
[math]|A|=5\cdot (-18)–(18)+3 \cdot 36[/math]
[math]|A|=-90-18+108=0[/math]
Il determinante di questa matrice è nullo. Questa matrice ha rango 2.
Per ulteriori approfondimenti sul rango di una matrice vedi qua
Proprietà del determinante di una matrice
Il determinante della matrice identità è[math]1[/math]
, qualunque sia l’ordine n della matrice.Se
[math]A[/math]
è una;- matrice triangolare superiore, in cui tutti gli elementi sotto la diagonale principale sono nulli;
- matrice triangolare inferiore, in cui tutti gli elementi sopra la diagonale principale sono nulli;
- matrice diagonale, in cui tutti gli elementi sopra e sotto la diagonale principale sono nulli;
[math]a_1, a_2, \ldots, a_n[/math]
gli elementi sulla diagonale, allora:
[math]\det(A) = a_1 \cdot a_2 \cdot \ldots \cdot a_n = \prod_{i=1}^n a_i[/math]
Se
[math]A[/math]
e [math]B[/math]
sono due matrici quadrate dello stesso ordine, allora il determinate del prodotto di due matrici è uguale al prodotto dei loro determinanti, per il teorema di Binet:
[math]\det(A B)= \det(A) \det(B)[/math]
Se
[math]\det(A) \neq 0[/math]
, e [math]B[/math]
è la matrice inversa di [math]A[/math]
, cioè tale che [math]AB=I[/math]
, allora:
[math]\det(A) = \frac{1}{\det(B)}[/math]
Se
[math]A[/math]
è una matrice quadrata con (almeno) una riga e/o una colonna nulla, allora [math]\det(A) = 0[/math]
. Se due righe, o due colonne, sono una multipla dell'altra, allora
[math]\det(A) = 0[/math]
. In generale se una riga (o una colonna) è data dalla combinazione lineare delle altre righe (o delle altre colonne), allora:
[math]\det(A) = 0[/math]
. Il determinante di una matrice quadrata coincide col determinante della sua trasposta:
[math]\det(A) = \det(A^T)[/math]
[math]A[/math]
è una matrice quadrata, e [math]B[/math]
è la matrice ottenuta moltiplicando una riga (o una colonna) di [math]A[/math]
per [math]\lambda \in \mathbb{\Re}[/math]
, allora:[math]det(B) = \lambda \det(A)[/math]
.Se
[math]A[/math]
è una matrice quadrata, e [math]B[/math]
è una matrice ottenuta da una riga (o una colonna) di [math]A[/math]
, un'altra riga (o colonna) eventualmente moltiplicata per [math]\lambda \in \mathbb{\Re}[/math]
, allora [math]\det(B) = \det(A)[/math]
.Se
[math]A[/math]
è una matrice quadrata, e [math]B[/math]
è una matrice ottenuta scambiando di posto due righe, o due colonne, di [math]A[/math]
, allora: [math]\det(B) = - \det(A)[/math]
.Se
[math]A[/math]
è una matrice quadrata di ordine [math]n \times n[/math]
allora, per ogni [math]\lambda \in \mathbb{\Re}[/math]
, vale:[math]\det(\lambda \cdot A) = \lambda^n \det(A)[/math]
Regola di Sarrus per calcolare il determinante
Il determinante di una matrice del terzo ordine può essere calcolato anche applicando il metodo di Sarrus. A partire da una matrice del tipo:
[math]A=\begin{pmatrix}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}[/math]
si riscrivono le prime due colonne a fianco della terza, ottenendo una matrice rettangolare:
[math]A=\begin{pmatrix}a_{11} & a_{12} & a_{13} & a_{11} & a_{12}\\ a_{21} & a_{22} & a_{23} & a_{21} & a_{22} \\ a_{31} & a_{32} & a_{33} & a_{31} & a_{32} \end{pmatrix} [/math]
Ora si eseguono i prodotti secondo le diagonali illustrate in figura, le nere verso destra e le rosse verso sinistra:
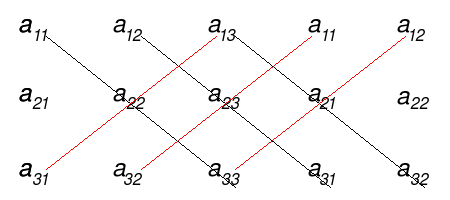
Alla somma dei termini ottenuti seguendo le diagonali nere, si sottrae quella ottenuta seguendo le diagonali rosse.
[math]\det(A)= a_{11} \cdot a_{22} \cdot a_{33} + a_{12} \cdot a_{23} \cdot a_{31} + a_{13} \cdot a_{21} \cdot a_{32} - a_{13} \cdot a_{22} \cdot a_{31} - a_{11} \cdot a_{23} \cdot a_{32} - a_{12} \cdot a_{21} \cdot a_{33} [/math]
Per ulteriori approfondimenti sul determinante vedi anche qua
