Si consideri una circonferenza di raggio
[math]R[/math]
centrata in [math]O = (0,0)[/math]
, e sia [math]P[/math]
un generico punto sulla circonferenza. 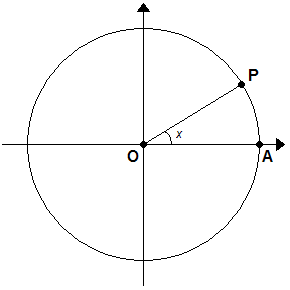
Comunque si fissi
[math]x in mathbb{R}[/math]
, si scelga [math]P[/math]
in modo che la misura (in radianti) dell'angolo [math]P hat{O} A[/math]
sia proprio [math]x[/math]
. Dette [math]P = (x_0, y_0)[/math]
le coordinate del punto [math]P[/math]
, si definiscono le funzioni goniometriche (seno, coseno, tangente, cotangente, secante, cosecante) come segue
[math]\\sin (x) = frac{y_0}{R} qquad \\cos(x) = frac{x_0}{R} qquad \text{tg}(x) = frac{\\sin(x)}{\\cos(x)} qquad \text{cotg}(x) = frac{\\cos(x)}{\\sin(x)} qquad \text{sec}(x) = frac{1}{\\cos(x)} qquad \text{\\cosec}(x) = frac{1}{\\sin(x)}[/math]
Relazione fondamentale della goniometria
[math]\\sin ^2(x) + \\cos^2(x) = 1[/math]
Conversione fra radianti e gradi
Se
[math]x[/math]
è la misura in radianti di un angolo, e [math]x^{circ}[/math]
è la rispettiva misura in gradi, si ha che
[math]x = frac{\pi}{180^{circ}} x^{circ} qquad x^{circ} = frac{180^{circ}}{\pi} x[/math]
Archi notevoli
[math]x[/math] (radianti) | [math]x^{circ}[/math] (gradi) | [math]\\sin (x)[/math] | [math]\\cos(x)[/math] | [math]\text{tg}(x)[/math] | [math]\text{cotg}(x)[/math] |
[math]0[/math] | [math]0^{circ}[/math] | [math]0[/math] | [math]1[/math] | [math]0[/math] | non esiste |
[math]frac{\pi}{12}[/math] | [math]15^{circ}[/math] | [math]frac{\sqrt{6} - \sqrt{2}}{4}[/math] | [math]frac{\sqrt{6} + \sqrt{2}}{4}[/math] | [math]2 - \sqrt{3}[/math] | [math]2 + \sqrt{3}[/math] |
[math]frac{\pi}{10}[/math] | [math]18^{circ}[/math] | [math]frac{\sqrt{5} - 1}{4}[/math] | [math]frac{1}{4} \sqrt{10 + 2 \sqrt{5}}[/math] | [math]\sqrt{frac{5 - 2 \sqrt{5}}{5}}[/math] | [math]\sqrt{5 + 2 \sqrt{5}}[/math] |
| [math]frac{\pi}{8}[/math] | [math]22^{circ} 30'[/math] | [math]frac{\sqrt{2 - \sqrt{2}}}{2}[/math] | [math]frac{\sqrt{2 + \sqrt{2}}}{2}[/math] | [math]\sqrt{2} - 1[/math] | [math]\sqrt{2} + 1[/math] |
[math]frac{\pi}{6}[/math] | [math]30^{circ}[/math] | [math]frac{1}{2}[/math] | [math]frac{\sqrt{3}}{2}[/math] | [math]frac{\sqrt{3}}{3}[/math] | [math]\sqrt{3}[/math] |
[math]frac{\pi}{5}[/math] | [math]36^{circ}[/math] | [math]frac{1}{4} \sqrt{10 - 2 \sqrt{5}}[/math] | [math]frac{\sqrt{5} + 1}{4}[/math] | [math]\sqrt{5 - 2 \sqrt{5}}[/math] | [math]\sqrt{frac{5 + 2 \sqrt{5}}{5}}[/math] |
[math]frac{\pi}{4}[/math] | [math]45^{circ}[/math] | [math]frac{\sqrt{2}}{2}[/math] | [math]frac{\sqrt{2}}{2}[/math] | [math]1[/math] | [math]1[/math] |
[math]frac{3 \pi}{10}[/math] | [math]54^{circ}[/math] | [math]frac{\sqrt{5} + 1}{4}[/math] | [math]frac{1}{4} \sqrt{10 - 2 \sqrt{5}}[/math] | [math]\sqrt{frac{5 + 2 \sqrt{5}}{5}}[/math] | [math]\sqrt{5 - 2 \sqrt{5}}[/math] |
[math]frac{\pi}{3}[/math] | [math]60^{circ}[/math] | [math]frac{\sqrt{3}}{2}[/math] | [math]frac{1}{2}[/math] | [math]\sqrt{3}[/math] | [math]frac{\sqrt{3}}{3}[/math] |
| [math]frac{3 \pi}{8}[/math] | [math]67^{circ} 30'[/math] | [math]frac{\sqrt{2 + \sqrt{2}}}{2}[/math] | [math]frac{\sqrt{2 - \sqrt{2}}}{2}[/math] | [math]\sqrt{2} + 1[/math] | [math]\sqrt{2} - 1[/math] |
[math]frac{2 \pi}{5}[/math] | [math]72^{circ}[/math] | [math]frac{1}{4} \sqrt{10 + 2 \sqrt{5}}[/math] | [math]frac{\sqrt{5} - 1}{4}[/math] | [math]\sqrt{5 + 2 \sqrt{5}}[/math] | [math]\sqrt{frac{5 - 2 \sqrt{5}}{5}}[/math] |
| [math]frac{5 \pi}{12}[/math] | [math]75^{circ}[/math] | [math]frac{\sqrt{6} + \sqrt{2}}{4}[/math] | [math]frac{\sqrt{6} - \sqrt{2}}{4}[/math] | [math]2 + \sqrt{3}[/math] | [math]2 - \sqrt{3}[/math] |
[math]frac{\pi}{2}[/math] | [math]90^{circ}[/math] | [math]1[/math] | [math]0[/math] | non esiste | [math]0[/math] |
Archi associati
Si possono ricavare i valori di seno, coseno, e delle altre funzioni goniometriche relativamente ad altri angoli notevoli mediante le formule seguenti
[math]\\cos(\pi + x) = - \\cos(x)[/math] | [math]\\sin (\pi + x) = - \\sin(x)[/math] | [math]\text{tg}(\pi + x) = \text{tg}(x)[/math] |
[math]\\cos(\pi - x) = - \\cos(x)[/math] | [math]\\sin (\pi - x) = \\sin(x)[/math] | [math]\text{tg}(\pi - x) = - \text{tg}(x)[/math] |
[math]\\cos(frac{\pi}{2} + x) = - \\sin (x)[/math] | [math]\\sin (frac{\pi}{2} + x) = \\cos(x)[/math] | [math]\text{tg}(frac{\pi}{2} + x) = - \text{cotg}(x)[/math] |
[math]\\cos(frac{\pi}{2} - x) = \\sin (x)[/math] | [math]\\sin (frac{\pi}{2} - x) = \\cos(x)[/math] | [math]\text{tg}(frac{\pi}{2} - x) = \text{cotg}(x)[/math] |
[math]\\cos(-x) = \\cos(x)[/math] | [math]\\sin (-x) = - \\sin(x)[/math] | [math]\text{tg}(-x) = - \text{tg}(x)[/math] |
Relazioni fra funzioni goniometriche di uno stesso arco
[math]\\cos^2(x) = frac{1}{1 + \text{tg}^2(x)} qquad \\sin ^2(x) = frac{\text{tg}^2(x)}{1 + \text{tg}^2(x)}[/math]
Formule di addizione e di sottrazione
[math]\\cos(x - y) = \\cos(x) \\cos(y) + \\sin (x) \\sin(y)[/math]
[math]\\cos(x + y) = \\cos(x) \\cos(y) - \\sin (x) \\sin(y)[/math]
[math]\\sin (x - y) = \\sin(X) \\cos(y) - \\sin(y) \\cos(x)[/math]
[math]\\sin (x + y) = \\sin(x) \\cos(y) + \\sin(y) \\cos(x)[/math]
[math]\text{tg}(x + y) = frac{\text{tg}(x) + \text{tg}(y)}{1 - \text{tg}(x) \text{tg}(y)}[/math]
[math]\text{tg}(x - y) = frac{\text{tg}(x) - \text{tg}(y)}{1 + \text{tg}(x) \text{tg}(y)}[/math]
[math]\text{cotg}(x + y) = frac{\text{cotg}(x) \text{cotg}(y) - 1}{\text{cotg}(x) + \text{cotg}(y)}[/math]
[math]\text{cotg}(x - y) = frac{\text{cotg}(x) \text{cotg}(y) + 1}{\text{cotg}(y) - \text{cotg}(x)}[/math]
Formule di duplicazione
[math]\\sin (2x) = 2 \\sin(x) \\cos(x) qquad \\cos(2x) = \\cos^2(x) - \\sin^2(x) = 2 \\cos^2(x) - 1 = 1 - 2 \\sin^2(x)[/math]
[math]\text{tg}(2x) = frac{2 \text{tg}(x)}{1 - \text{tg}^2(x)} qquad \text{cotg}(2x) = frac{\text{cotg}^2(x) - 1}{2 \text{cotg}(x)}[/math]
Formule di triplicazione
[math]\\sin (3 x) = 3 \\sin(x) - 4 \\sin^3(x) qquad \\cos(3x) = 4 \\cos^3(x) - 3 \\cos(x) qquad \text{tg}(3x) = frac{3 \text{tg}(x) - \text{tg}^3(x)}{1 - 3 \text{tg}^2(x)}[/math]
Formule di prostaferesi
[math]\\sin (p) + \\sin(q) = 2 \\sin(frac{p+q}{2}) \\cos(frac{p-q}{2})[/math]
[math]\\sin (p) - \\sin(q) = 2 \\sin(frac{p-q}{2}) \\cos(frac{p+q}{2})[/math]
[math]\\cos(p) + \\cos(q) = 2 \\cos(frac{p+q}{2}) \\cos(frac{p-q}{2})[/math]
[math]\\cos(p) - \\cos(q) = -2 \\sin (frac{p+q}{2}) \\sin (frac{p-q}{2})[/math]
Formule di Werner
[math]\\sin (x) \\cos(y) = frac{1}{2} [\\sin(x - y) + \\sin(x + y)][/math]
[math]\\sin (x) \\sin(y) = frac{1}{2} [\\cos(x - y) - \\cos(x + y)][/math]
[math]\\cos(x) \\cos(y) = frac{1}{2} [\\cos(x - y) + \\cos(x + y)][/math]
Formule di bisezione
[math]\\sin ^2(x) = frac{1 - \\cos(2x)}{2} qquad \\cos^2(x) = frac{1 + \\cos(2x)}{2}[/math]
[math]\text{tg}(x) = frac{1 - \\cos(2x)}{\\sin (2x)} = frac{\\sin(2x)}{1 + \\cos(2x)}[/math]
[math]\text{cotg}(x) = frac{1 + \\cos(2x)}{\\sin (2x)} = frac{\\sin(2x)}{1 - \\cos(2x)}[/math]
Formule parametriche
Formule parametriche
[math]\\sin (x) = frac{2 \text{tg}(frac{x}{2})}{1 + \text{tg}^2(frac{x}{2})} qquad \\cos(x) = frac{1 - \text{tg}^2(frac{x}{2})}{1 + \text{tg}^2(frac{x}{2})}[/math]
[math]\text{tg}(x) = frac{2 \text{tg}(frac{x}{2})}{1 - \text{tg}^2(frac{x}{2})} qquad \text{cotg}(x) = frac{1 - \text{tg}^2(frac{x}{2})}{2 \text{tg}(frac{x}{2})}[/math]




