Spirale
Una spirale è una curva che si avvolge attorno ad un punto fisso, detto polo della spirale.
Spirale archimedea
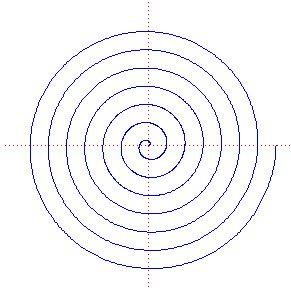
Equazione in forma polare: dati
ho = a + b heta[/math]
Distanza fra i bracci: in una spirale archimedea la distanza fra i bracci vale
Spirale iperbolica
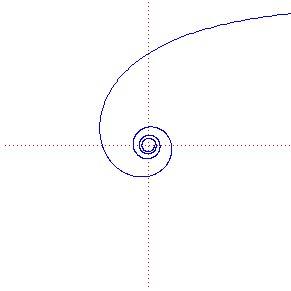
Equazione in forma polare: dato
us {0}[/math]
ho heta = a[/math]
Equazione parametrica: l'equazione parametrica di una spirale iperbolica è
us {0}[/math]
Asintoto: una spirale iperbolica, di equazione in forma polare o parametrica come le precedenti, ammette come asintoto la retta di equazione
Spirale logaritmica
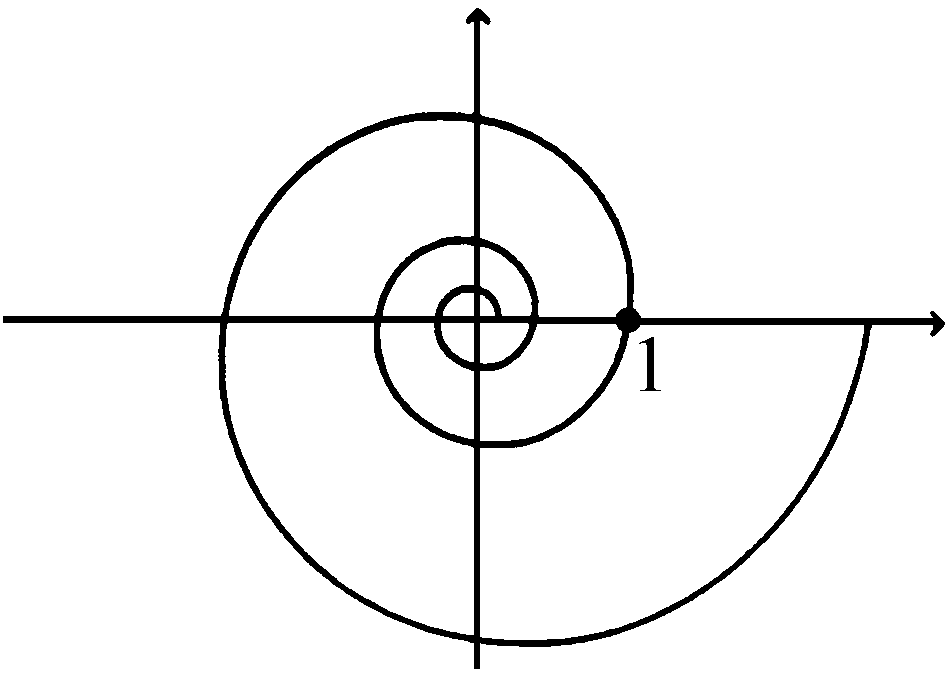
Equazione in forma polare: dati
us {0}[/math]
us {0, 1}[/math]
ho = a b^{ heta}[/math]
o equivalentemente
ho}{a})[/math]
Equazione parametrica: l'equazione parametrica di una spirale logaritmica è
Trattrice
La trattrice è una curva in cui i segmenti tra una curva e una data retta risultano di ugual misura.
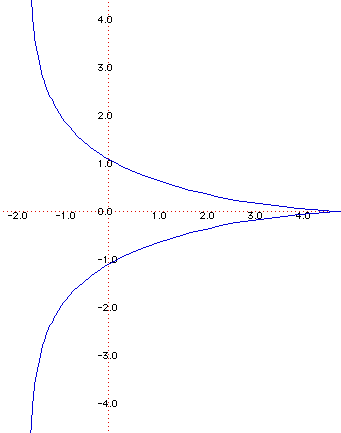
Equazione trigonometrica: l'equazione in forma trigonometrica di una trattrice con la cuspide nel punto
Equazione iperbolica: l'equazione in forma iperbolica di una trattrice con la cuspide in
Equazione differenziale: una trattrice con la cuspide in
Asintoto: una trattrice, avente come equazione una delle precedenti, ammette come asintoto la retta di equazione
Lunghezza di un arco: la lunghezza di un arco di trattrice individuato dalle rette di equazione
Area: l'area compresa fra la trattrice e il suo asintoto è
