Errore di troncamento formula di Taylor

Buonasera a tutti,

Sto studiando il metodo delle differenze finite. Il testo di riferimento fa un breve richiamo al teorema di Taylor:
Dalla formula di Taylor con resto di Lagrange: $f(x)=\sum_{k=0}^\infty f^k(x)/(k!)(x-x_0)^k+O(x-x_0)^(k+1)\star$.
Vista così, non mi torna il modo in cui viene stimato l'errore.
Si consideri a titolo d'esempio lo sviluppo di McLaurin di $sin(x)$ (quanto segue vale per una qualsiasi funzione analitica):

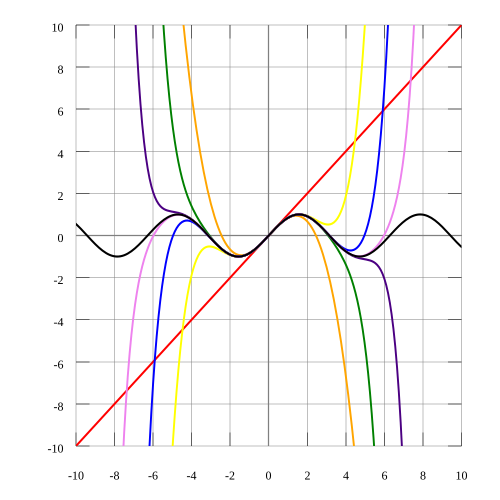
È chiaro come l'intervallo in cui il polinomio di McLaurin converge alla funzione reale cresca al crescere dell'ordine. Il polinomio del settimo ordine (curva verde) bene approssima la funzione tra $-pi$ e $+pi$. Evidentemente l'errore commesso valutando la funzione in $pi$ con il polinomio del 7 ordine è inferiore a quello commesso valutandola con il polinomio del quinto ordine (curva gialla). Eppure, dalla $\star$, il primo risulta essere di due ordini di grandezza superiore al secondo. Insomma, per $x-x_0<1$ i conti tornano e in effetti all'aumentare dell'ordine decresce l'errore, ma per $x-x_0>1$ vale il contrario. È come se la $\star$ valesse soltanto per $x-x_0<1$.
Dove sbaglio?

Ciao emiglio, benvenut* sul forum!

Non c'è niente di strano. Sia \(\text{O}\)-grande sia \(\text{o}\)-piccolo sono stime locali: valgono in un intorno di \(x_0\). Hai che \(f\) è un \(\text{O}(g)\) per \(x \to x_0\) se esistono \(M>0\) e \(\delta>0\) tali che \(|f(x)| \le Mg(x)\) per ogni \(x \in (x_0-\delta,x_0+\delta)\) (ovviamente, dove tutto ciò che è scritto è definito).

Ciao emiglio,

Benvenuto sul forum!

Dove sbaglio?

E' sbagliata la formula di Taylor, quella corretta è la seguente:

$ f(x)=\sum_{k=0}^{n} (f^{(k)}(x))/(k!) (x-x_0)^k+O(x-x_0)^(n+1) $

@emiglio: Scusa, ma quello è proprio il Teorema del resto nella forma di Lagrange "scritto peggio".

Il teorema ti dice che, soddisfatte ipotesi tecniche, chiamato $T_{f,n,x_0} (x)$ il polinomio di Taylor di ordine $n$ centrato in $x_0$ relativo ad $f$, hai che esiste un numero $xi$ nell'intervallo di estremi $x$ ed $x_0$:
\[
f(x) - T_{f,n,x_0}(x) = \frac{1}{(n+1)!} f^{(n+1)}(\xi)\cdot (x - x_0)^{n+1}\; ;
\]
se $f^((n+1))$ è limitata in un intorno di $x_0$ da una costante $M >= 0$, prendendo $x$ in tale intorno hai:
\[
\Big| f(x) - T_{f,n,x_0}(x) \Big| \leq \frac{M}{(n+1)!} \cdot |x - x_0|^{n+1}
\]
e questa è la definizione di O-grande (vedi qui), sicché:
\[
\Big| f(x) - T_{f,n,x_0}(x) \Big| = \operatorname{O}\left( (x - x_0)^{n+1}\right)\; .
\]

Inoltre, ti sconsiglio vivamente di provare a ragionare con gli sviluppi di MacLaurin delle funzioni goniometriche, perché contengono troppi addendi nulli che mascherano quello che vuoi vedere.


P.S.: Controlla un po' gli estremi di quella sommatoria.

Tutto chiaro, confondevo il concetto di O grande con quello di ordine di grandezza dell'errore. Grazie a tutti!

Continua a non essermi chiara una cosa. Posto $x-x_0>1$, dato che $(x-x_0)^(k+1)/((k+1)!)$ è crescente per $0<=k+1<=(x-x_0)$, affinché l'errore decresca al crescere dell'ordine di sviluppo, per $x\in[0,x-x_0]$ il termine $f^(k+1)(\xi)$ deve tendere a zero in più velocemente di quanto $(x-x_0)^(k+1)/((k+1)!)$ tende ad infinito per $k\to\infty$. Non so se mi spiego. In sostanza, se ignoro la derivata, non è sempre vero che l'errore decresce al crescere dell'ordine, dunque la derivata deve compensare tale fenomeno. Sbaglio qualcosa? Tale problema non si pone $x-x_0<1$.

Se $x$ ed $x_0$ sono fissati, sei sicuro che $ (x-x_0)^(k+1)/((k+1)!) -> oo$ per $k -> oo$?

Forse mi sono spiegato male, il formalismo non è il mio forte. Volgarmente quello che intendo dire è che affinché l’errore decresca il contributo decrescente dato dalla derivata deve vincere su quello crescente dato dal passo, questo nell’intervallo in cui quest’ultimo è appunto crescente. Altrimenti c’è un intervallo in cui l’errore cresce al crescere dell’ordine.