Quadratino

Un piccolo quadrato è costruito all'interno di un quadrato $ABCD$ di lato unitario in questo modo: dividere ogni lato del quadrato unitario in $n$ parti uguali e quindi connettere i suoi vertici con i punti di divisione più vicini ai vertici opposti.



Determinare $n$ in modo tale che l'area del piccolo quadrato sia pari esattamente a $1/1985$.


Cordialmente, Alex

Testo nascosto, fai click qui per vederlo

In riferimento alla seguente figura:

\(\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\)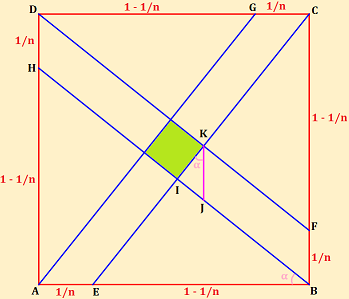

sia ha: \[
\overline{IK} \equiv \frac{1}{\sqrt{1985}},
\quad \quad
\overline{JK} \equiv \frac{1}{n},
\quad \quad
\cos(\alpha) \equiv \frac{1}{\sqrt{1^2+\left(1-\frac{1}{n}\right)^2}}
\] per cui:\[
\overline{IK} = \overline{JK}\cos(\alpha)
\quad \Leftrightarrow \quad n = 32\,.
\]

Bene!

Ma senza trigonometria?



Cordialmente, Alex

Ma senza trigonometria?

Testo nascosto, fai click qui per vederlo

I triangoli \(ABH\) e \(IJK\) sono simili per il primo criterio di similitudine, quindi: \[
\frac{1/\sqrt{1985}}{1} = \frac{1/n}{\sqrt{1^2+\left(1-\frac{1}{n}\right)^2}}
\quad \quad \Leftrightarrow \quad \quad n = 32\,.
\] In tal modo ho riciclato l'equazione di ieri.

Non sto a controllare, non è ora

Testo nascosto, fai click qui per vederlo

La soluzione e' gia' stata data.
Aggiungo un'impostazione alternativa per arrivare al risultato.
Chiamo $x$ la quantita' $1-1/n$, che individua un segmento su ciascuno dei lati.

Nella figura si possono individuare dei triangoli rettangoli T1 i cui cateti misurano $1$ e $x$.
L'ipotenusa e' quindi $\sqrt(1+x^2)$ e l'area e' $x/2$.
Poi si possono individuare dei triangoli rettangoli T2 simili ai T1 (condividono un angolo non retto) la cui ipotenusa misura $x$.
Per similitudine ai T1 l'area dei T2 sara' $x^3/(2(1+x^2))$.
Sempre nella figura ci sono poi 2 strisce "oblique" S di area $1-x$.
L'intersezione delle due strisce S e' il quadratino di area Q.
Il quadrato ABCD puo' essere composto da 4 triangoli T2, due strisce S, a cui sottrarre il quadratino Q.
In termini di aree:

$ABCD = 1= 4 x^3/(2(1+x^2)) + 2 (1-x) - Q$

Semplificando si arriva a

$x^2 + 2/(Q-1) x +1 = 0$

da cui ricavare $x$ conoscendo $Q = 1/1985$ e poi $n = 1 / (1-x)$