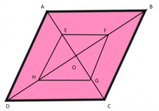
Cos'è un parallelogramma e come riconoscerlo
Il parallelogramma è un poligono, ossia è formato da una parte di spazio racchiuso all'interno di una linea spezzata chiusa. Quest'ultima è costruita a partire da segmenti consecutivi di lunghezze differenti, in cui il primo estremo coincide con l'ultimo. Tali segmenti prendono il nome di lati e gli estremi si chiamano vertici. La porzione di spazio definita da due lati, invece, viene definito angolo.
In particolare, il parallelogramma appartiene alla sottocategoria dei quadrilateri. Un quadrilatero è un poligono che presenta quattro lati, quattro vertici e quattro angoli. La somma dei suoi angoli interni, inoltre, ammonta a un angolo giro.
In realtà, quando si parla di parallelogrammi si fa riferimento a un gruppo di quadrilateri che include delle figure molto note.
Le proprietà che permettono di distinguere un parallelogramma dalle altre figure sono le seguenti:
- le diagonali si incontrano nel loro punto medio. Ciò significa che si dividono reciprocamente in due segmenti congruenti
- la somma di due angoli interni consecutivi ammonta a [math]180°[/math]
- le coppie di angoli interni opposti hanno uguale ampiezza
- i lati opposti sono paralleli e congruenti
Alla luce di queste informazioni, possono essere considerati dei parallelogrammi:
- i quadrati, poiché sono dei parallelogrammi aventi tutti i lati e tutti gli angoli uguali
- i rettangoli, che sono dei parallelogrammi aventi solo gli angoli congruenti
- i rombi, cioè parallelogrammi aventi solo i lati congruenti
- i trapezi: se, infatti, consideriamo le possibili altezze del parallelogramma è possibile individuare un trapezio
Come calcolare il perimetro e l'area del parallelogramma
Dopo aver compreso le proprietà e le caratteristiche principali dei parallelogrammi, è necessario fare un ulteriore step prima di passare alla risoluzione dei problemi: l'introduzione delle formule.Le formule dirette del parallelogramma sono finalizzate al calcolo del perimetro e dell'area del parallelogramma. La prima grandezza corrisponde alla somma della lunghezza dei lati che compongono il contorno della figura, la seconda, invece, all'estensione della superficie racchiusa al suo interno. Le formule inverse, invece, permettono di calcolare, avendo note una delle due grandezze precedentemente citate, la lunghezza dell'altezza o del lato.
In termini matematici si ha che:
- il perimetro può essere calcolato come [math]2p=2l+2b[/math], in cui[math]l,b[/math]sono i lati. Se, ad esempio, il parallelogramma considerato è un quadrato si ha che[math]l=b[/math]e che quindi[math]2p=4l[/math]
- l'area può essere calcolata come [math]A=bh[/math]. Per i quadrati vale che[math]l=b=h[/math], quindi[math]A=l^2[/math]
- la lunghezza del lato è calcolabile sia a partire dal perimetro che a partire dall'area. Nel caso del perimetro si ha che [math]b=\frac{p-2b}{2}[/math], mentre nel caso dell'area si ha che[math]b=\frac{A}{h}[/math]
Esempio svolto: calcola l'area del parallelogramma
Il pavimento di una stanza ampio[math]20 m^2[/math]
dev'essere ricoperto utilizzando delle mattonelle. La forma delle mattonelle può essere paragonata a quella di un generico parallelogramma.Considerando che:
- l'altezza è pari a [math]20 cm[/math]
- la base sia lunga [math]40 cm[/math]
- il lato obliquo è pari ai [math]\frac{3}{2}[/math]dell'altezza
Calcola il numero di mattonelle necessarie a coprire l'intera stanza e il perimetro della singola mattonella.
Svolgimento commentato del problema
Per valutare il numero di mattonelle necessarie a coprire l'intera stanza è necessario vedere quante volte l'area di una singola mattonella "entra" nell'area dell'intera stanza. Per questo motivo l'operazione da effettuare è una divisione avente come numeratore l'estensione dell'intera stanza e come denominatore l'ampiezza della singola mattonella. Per avere il risultato in metri, converto tutte le lunghezze.
[math]20 cm=0.20 m[/math]
[math]40 cm=0.40 m[/math]
L'area della singola mattonella ammonta a
[math]A=0.20\cdot0.40=0.08 m^2[/math]
Quindi il numero di mattonelle necessarie sarà [math]\frac{20 m^2}{0.08 m^2}=250[/math]
Per coprire il pavimento dell'intera stanza sono necessarie
[math]250[/math]
mattonelle. Al fine di calcolare il perimetro di un'unica mattonella calcolo la lunghezza del lato obliquo [math]l=\frac{3}{2}\cdot 20 cm= 30 cm[/math]
. Il perimetro della singola mattonella è
[math]2p=0.20\cdot 2 + 0.40\cdot 2=0.40+0.80=1.20 m[/math]
.Per ulteriori approfondimenti sui parallelogrammi vedi anche qua
