Il software Cabri géomètre è stato sviluppato da Y. Baulac, F. Bellemain e J. M. La Borde presso l'Università di Grenoble (la prima versione del software risale al 1988, la versione più recente è la Cabri II plus del 2003) come supporto all'insegnamento della geometria euclidea. Nelle ultime versioni è stato implementato l'uso delle coordinate cartesiane per integrare l'approccio sintetico con quello analitico.
Il programma utilizza lo schermo del computer come un foglio di disegno, ha una barra di strumenti tipici della geometria euclidea e del disegno su carta: punti, rette, segmenti, poligoni, compasso, misure di segmenti, di angoli, di aree, ...
Questi strumenti permettono di disegnare sul monitor in modo abbastanza simile a come si disegna su carta con matita, riga e compasso.Non si tratta di una simulazione come finzione, ma di un uso concettuale degli strumenti elementari: per disegnare una retta l'allievo deve indicare un punto, gli compare una retta mobile ma vincolata al punto, l'allievo 'vede' un fascio di rette e ha un'idea immediata di un concetto abbastanza complesso da intuire, quindi deve indicare un secondo punto per fissare la retta, si rende conto che due punti individuano una retta; per disegnare una circonferenza l'allievo indica prima il centro e poi il raggio; e così via.
L'idea innovativa del software, che è ciò che lo rende particolarmente interessante a fini didattici, è la possibilità di agire sulla figura costruita muovendo, con il trascinamento del mouse, i punti 'liberi' della costruzione: l'allievo può osservare ciò che resta inalterato e ciò che varia. Rispetto al disegno su carta lo studente si rende conto delle relazioni tra gli enti geometrici realizzati: appartenenza di un punto a una retta, perpendicolarità o parallelismo tra rette, ecc.
Interfaccia utente
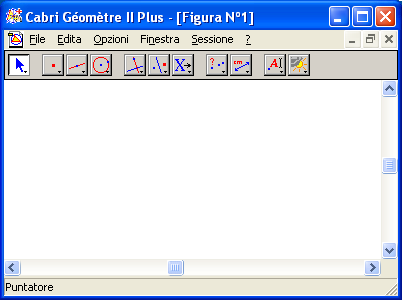
Barra dei menu:
File contiene i principali comandi per l'uso dei file (aprire, chiudere, salvare, stampare) ma anche la possibilità di visualizzare l'intera area di disegno.
Edita permette anche di ripetere passo passo la costruzione geometrica.
Opzioni permette di personalizzare la finestra di lavoro.
Finestra permette di agire sulla finestra di lavoro e modificarne le impostazioni.
Sessione permette di registrare la sessione di lavoro.
Barra degli strumenti:
![]()
Puntatore: permette di modificare gli oggetti disegnati trascinando alcuni o tutti gli elementi della costruzione.
Punto: per disegnare un punto che può essere libero, può essere vincolato a restare su un luogo geometrico, può essere il punto di intersezione di due luoghi geometrici.
Retta: permette di disegnare elementi rettilinei: rette, semirette, segmenti, vettori, triangoli, poligoni e poligoni regolari.
Circonferenza: permette di disegnare circonferenze, archi di circonferenze e coniche.
Costruzioni: permette di disegnare elementi ottenuti da costruzioni geometriche: retta perpendicolare a una retta data, retta parallela, punto medio, asse, bisettrice, luoghi,…
Trasformazioni: permette di applicare trasformazioni geometriche di base: simmetria assiale, simmetria centrale, traslazione, rotazione, omotetia, inversione.
Macro: per realizzare nuove costruzioni di base da poter utilizzare semplicemente richiamandole.
Verifica: per verificare se gli elementi della costruzione soddisfano alcune proprietà come l'allineamento di punti, il parallelismo e la perpendicolarità di rette, l'equidistanza e l'appartenenza.
Misura: per effettuare misure sugli oggetti geometrici della costruzione: lunghezze, aree, inclinazioni, angoli, coordinate, …
Visualizza: permette di contrassegnare gli elementi della costruzione: assegnare nomi, aggiungere del testo esplicativo, segnare un angolo; permette anche di animare la costruzione.
Disegna: contiene i principali strumenti per personalizzare il disegno: mostrare o nascondere alcuni elementi della costruzione, per esempio i passaggi intermedi, aggiungere il bottone mostra/nascondi, modificare i colori e il tratteggio del disegno; mostrare gli assi cartesiani.
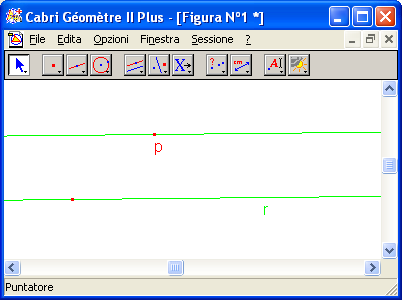
Esempio 1
Per un punto esterno a una retta disegnare la parallela alla retta e passante per il punto dato.
1. Disegnare la retta con lo strumento Retta.
2. Assegnare il nome r alla retta con lo strumento Visualizza.
3. Disegnare un punto esterno alla retta con lo strumento Punto.
4. Assegnare il nome al punto con lo strumento Visualizza.
5. Attivare dallo strumento Costruzioni lo strumento Retta parallela, indicare con il puntatore la retta r e poi il punto P.
Esempio 2
Costruire la retta di Eulero di un triangolo. Questo disegno è praticamente impossibile da realizzare non solo sulla lavagna ma anche su carta con riga e squadrette.
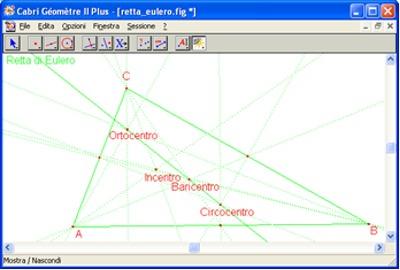
Cabri, quindi può essere utilizzato come una lavagna di precisione, con elevato grado di leggibilità dei disegni.
Quando e come usarlo a scuola
Il software non vincola a percorsi didattici prefissati, può essere utilizzato liberamente per trattare quasi tutti gli argomenti della geometria elementare e può anche essere usato semplicemente come lavagna luminosa.
Scuola primaria: disegno di punti, rette, poligoni, circonferenze, lunghezze e aree
Scuola secondaria di 1° grado: tutti gli argomenti di geometria piana, incluse le trasformazioni geometriche
Scuola secondaria di 2° grado: tutti gli argomenti di geometria sintetica del biennio, geometria analitica, rappresenta di funzioni e di luoghi geometrici nel triennio.
Costi e licenze
Produttore: Cabri Geometry II è un marchio registrato presso l'Universitè Joseph Fourier di Grenoble (Francia) Distributore: Texas Instruments Distributore italiano: Campustore Siti di riferimento:
http://education.ti.com/us/product/software.html
Licenze: commerciale; la versione Demo è scaricabile liberamente ma non ha abilitata la funzione di salvare le costruzioni
Lingua: In diverse lingue, anche in italiano.
Requisiti tecnici: Esiste la versione per Windows e quella per Macintosh
Manuali e guide: Cabri Manuale, http://education.ti.com/downloads/guidebooks/it/gbbook_ita.pdf
Per altri manuali didattici consulta la bibliografia.
La guida in linea del programma è attivabile dal tasto F1, nella parte inferiore della finestra di lavoro compare il suggerimento relativo allo strumento che si deve usare.
Estensione dei file prodotti e supportati
Le costruzioni possono essere salvate, i file hanno estensione .fig e grandezza introno ai 5 KB.
E' possibile anche salvare delle Macro, ossia delle costruzioni di base che possono essere richiamate nella costruzione di una figura più complessa. Per esempio, è possibile salvare una Macro che disegni un quadrato di lato assegnato e richiamare la macro nelle costruzioni che fanno uso di uno o più quadrati. L'estensione dei file macro è .mac, la dimensione di questo file è di 1KB o poco più.
E' possibile produrre Applet Java, ma solo con la versione precedente del programma, la Cabri II.
Bibliografia
Green D., 1994, Cabri-géomètre, la rivincita di Euclide, Quaderni CabrIRRSAE (n. 1), a cura dell'IRRE Emilia Romagna.
L'autore mette in evidenza le motivazioni che hanno portato alla realizzazione del software Cabri e gli usi didattici, l'articolo fa riferimento a una delle prime versioni di Cabri, ma è utile per capire lo spirito del programma. “Il grido dei moderni movimenti matematici agli inizi degli anni '60 era "Abbasso Euclide!" Un software di pregio chiamato Cabri-géomètre potrebbe invertire l'abbandono della geometria euclidea nelle scuole”.
CabriIRRSAE, 1994, Intervista a C. Laborde, CabrIRRSAE (n. 1, 1994), a cura dell'IRRE Emilia Romagna.
Intervista a Colette La Borde un membro dell'equipe che ha realizzato Cabri Géomètre
Paola D., 2004, “Software di geometria dinamica per un sensato approccio alla dimostrazione in geometria: un esempio di Laboratorio di Matematica”, in Progetto Alice (13), Pagine, Roma, pp. 103-121.
L'autore propone un'esperienza di laboratorio con l'uso di Cabri centrata sul valore didattico della dimostrazione in geometria. Il sensato approccio si riferisce ai sensi e quindi all'esperienza e alla percezione.
Boieri P., Dané C. , 2003, Geometria con Cabri, costruire, scoprire dimostrare, Loescher, Torino.
Manuale di geometria per la scuola secondaria di 2° grado che fanno uso di Cabri
R. Sabbadini, Fisicabri, Principato, Milano, 2005.
Simulazioni di argomenti di fisica (meccanica, termodinamica, onde e ottica, relatività, elettromagnetismo) ed esercizi di fisica con Cabri
AA. VV., Sperimentazione di didattica della matematica con Cabri, nella Scuola Media Statale Don Milani, Venaria Reale (TO)
Un percorso didattico sull'insegnamento della geometria con Cabri, completo di schede ed esercizi per gli studenti della scuola secondaria di 1° grado. Il percorso presentato è stato effettivamente realizzato in classe.
Di Stefano C., 2005, “Le trasformazioni geometriche e Cabri”, in Progetto Alice (16), Pagine, Roma, pp. 27-42.
L'autore presenta semplici attività da svolgere con Cabri su uno dei temi che maggiormente in risalto le potenzialità di questo software.
Cabrinews, http://www.fardiconto.it/cabrinews/
Lista di discussione frequentata principalmente da insegnati che condividono dubbi e proposte sull'uso di Cabri ma anche sui temi dell'insegnamento della matematica.
CabriIRRSAE, http://www.fardiconto.it/cabrirrsae/
Bollettino e Quaderni pubblicati on line e di libera consultazione. La pubblicazione tuttavia è ferma per mancanza di fondi al n.39 di Aprile 2004.
CabriJava, http://kidslink.scuole.bo.it/fardiconto/cabrijava/
Sito per le Applet Java che si possono ottenere con Cabri. E' possibile scaricare gratuitamente i componenti aggiuntivi per produrre le Applet, trovare indicazioni per la produzione di Applet, esempi.
Autore della scheda: Antonio Bernardo
Anno: 2005