| Passaggio #1 Dopo aver aperto il MAIN MENU, seleziona l'icona GRAPH. |  |
| Passaggio #2 Scrivi la funzione [math]y=-\sqrt\{abs(x)\}[/math]
selezionando OPTN , y (NUMERIC) , q (ABS).Premi w (CALC) e quindi q (D/DX). Inserisci la funzione scrivendo Y con il tasto q e poi 1. Sempre con f scrivi x nella casella di pedice. Inserisci quindi la seguente combinazione di tasti e opzioni: L , p, DERIVATIVE , ON , l , DRAW , SKETCH per disegnare la tangente. Sul display adesso è possibile visualizzare il grafico della funzione e quello della sua derivata. | 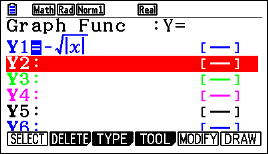
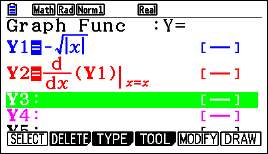 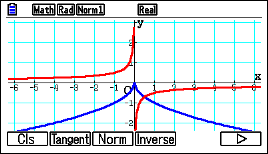 |
| Passaggio #3 Premendo w, sul display puoi leggere che nel punto O(0;0) la derivata non esiste. Ora, muovendoti prima con la freccia destra e poi sinistra, puoi disegnare le tangenti in punti prossimi a O. È possibile notare come i coefficienti angolari delle rette siano opposti e, quindi, nel punto O si avranno due tangenti con coefficienti ±∞. Il punto è quindi una cuspide. | 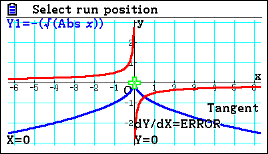
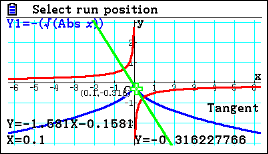 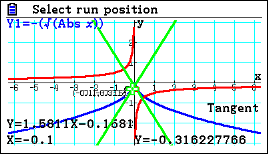 |
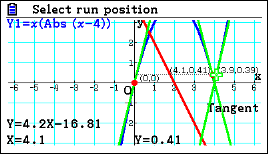
| Passaggio #4 Con gli stessi comandi usati nel passaggi #1 e #2, puoi rappresentare una funzione con un punto angoloso. Le tangenti sono due con coefficienti angolari finiti e di segno opposto. | 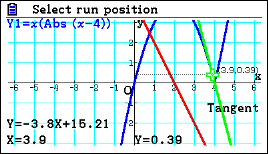
 |
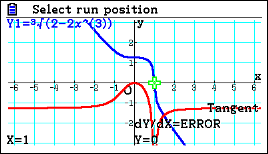
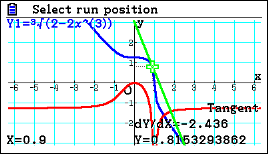
| Passaggio #5 Ora, sempre con gli stessi comandi usati precedentemente, puoi trovare un punto di flesso a tangente verticale. La funzione dell'esempio permette anche di far notare la differenza con un flesso a tangente orizzontale. | 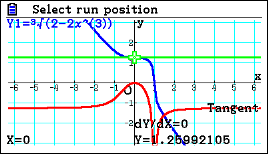
   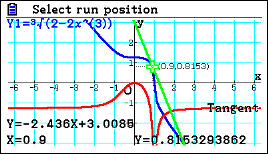 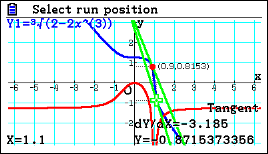 |

