I problemi di scelta, classico esempio di problem solving, consistono nell'utilizzo di equazioni o di altri concetti matematici nella vita quotidiana. Dopo aver affrontato l'argomento dei sistemi lineari di primo grado, può rivelarsi utile affrontarne in classe l'utilizzo dello stesso nella risoluzione di situazioni reali. Si tratta di un'attività che può essere interessante svolgere con l'ausilio di una calcolatrice, in modo tale da dedicare uno spazio più ampio al ragionamento proprio del problem solving.
Un esempio è rappresentato dal seguente esercizio, svolto con l'ausilio della calcolatrice grafica Casio FX-CG20.
Si è di fronte alla necessità di noleggiare per 18 mesi dei personal computer per il proprio ufficio: vengono prese in considerazione varie offerte:
A.
100 euro/mese per ogni personal computer;B. 300 euro una tantum per l'attivazione del contratto di noleggio e 50 euro/mese per personal computer;
C. 800 euro una tantum per l'attivazione del contratto di noleggio e 10 euro/mese per personal computer.
In base a quale criterio il direttore sceglierà l'offerta, non volendo spendere più di 1200 euro?
Dal punto di vista strettamente matematico le tre proposte sono rappresentate da altrettante equazioni:
Y1 = 100 x
Y2 = 300 + 50 x
Y3 = 800 + 10 x.
Inoltre, devono essere confrontate con la soglia massima dei 1200 euro, rappresentata a sua volta dall'equazione Y4 = 1200.
| Passaggio #1 Seleziona GRAPH dal MAIN MENU; comparirà la schermata nella quale inserire le equazioni. Inserisci le equazioni e, per ognuna, premi l. Premi il tasto u corrispondente alla funzione DRAW. |
|
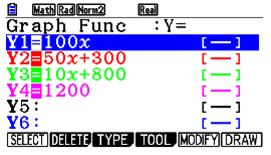 | |
| Passaggio #2 Compare il grafico con le 4 equazioni: attraverso i colori si distinguono le 4 equazioni. | 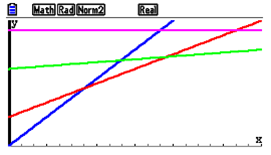 |
| Passaggio #3 È ora utile, ai fini della comprensione del risultato reale, conoscere i punti di intersezione tra le rette. Affronteremo il calcolo di tutte le intersezioni interessanti ai fini del risultato del problema. Premi il tasto y per visualizzare il menu nella parte bassa del display. Premi nuovamente y corrispondente alla funzione INTSECT. | 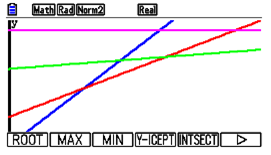 |
| Passaggio #4 A questo punto, vista la presenza di quattro grafici, si devono selezionare le due equazioni di cui si vuole conoscere il punto di intersezione. Poiché si vuole conoscere l'intersezione tra Y1 ed Y2, si procederà alla loro selezione. Inizierà a lampeggiare il grafico di Y1: selezionalo premendo il tasto l. Inizierà a lampeggiare il grafico di Y2: selezionalo premendo il tasto l. Premendo due volte l compaiono le coordinate del punto di intersezione delle equazioni Y1 ed Y2. | 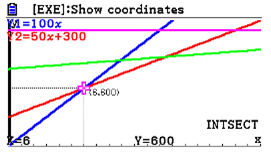 |
| Passaggio #5 Ripeti le operazioni svolte nel passo precedente, selezionando questa volta la Y2 e la Y3. Premendo due volte l compaiono le coordinate del punto di intersezione delle equazioni Y2 ed Y3. | 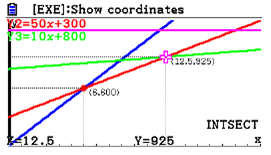 |
| Passaggio #6 Ripeti le operazioni svolte nel passo precedente, selezionando questa volta la Y2 e la Y4. Premendo due volte l compaiono le coordinate del punto di intersezione delle equazioni Y2 ed Y4. | 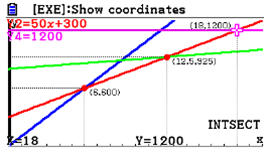 |
| Passaggio #7 Risulta utile conoscere il valore che assume Y3 in 18, poiché sarà la spesa per i 18 mesi di noleggio. Procedi valutando Y3 in 18. Premi y e si aprirà il menù come quello a fianco. | 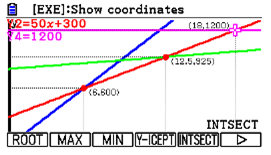 |
| Passaggio #8 Da questo menù premi u per scorrere alle altre voci del menu. Premi il tasto q relativo alla funzione Y-CAL. | 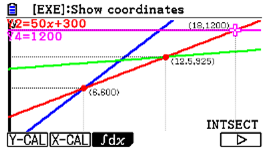 |
| Passaggio #9 Ti viene richiesto di selezionare la funzione tra le quattro di cui vuoi conoscere il valore in una certa X. Scegli la Y3 utilizzando il cursore presente sulla tastiera. | 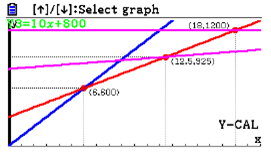 |
| Passaggio #10 Viene richiesto di inserire il valore di X di cui vuoi conoscere il corrispondente Y: inserisci 18. | 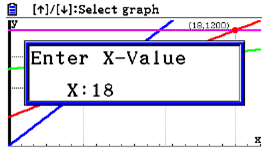 |
| Passaggio #11 Premendo due volte il tasto l compariranno le coordinate del punto richiesto. | 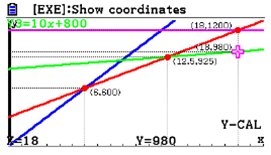 |
L'esercizio termina affermando quanto segue:
per 18 mesi è conveniente la proposta 3, il cui costo complessivo è di 980 euro.
Anche la proposta 2 si mantiene entro la soglia di spesa prevista, ma è certamente meno vantaggiosa.
La discussione grafica ci permette di commentare quanto segue:
…¢ nei primi sei mesi sarebbe stato da preferire la prima proposta;
…¢ dal sesto al dodicesimo mese sarebbe stato da preferire la seconda proposta.