[math]\\pi/12[/math]
. Applicando la formula del teorema del coseno e la sua inversa, otterremo rispettivamente le dimensioni del terzo lato e degli altri due angoli; per comodità e maggiore comprensione dei risultati converti l'angolo noto in gradi: [math]\\pi/12 rad=15°[/math]
. La comodità di questo procedimento sta nel fatto di poter attribuire ai valori iniziali infiniti valori di lati e angoli.| Passaggio #1 Premi il tasto RUN-MATRIX dal MAIN MENU. |  |
| Passaggio #2 Attribuisci il valore di un lato ad una variabile d'appoggio A Usa il tasto b come mostrato nello screenshot: a questo punto la variabile A contiene il valore 3. |  |
| Passaggio #3 Attribuisci il valore dell'altro lato alla variabile d'appoggio B. |  |
| Passaggio #4 Attribuisci il valore dell'angolo noto alla variabile d'appoggio [math] h\eta[/math] . |  |
| Passaggio #5 A questo punto presta attenzione nell'inserimento della formula nel modo corretto [math](A^2+B^2+2AB \\cos h\eta )^{1/2} = C[/math]
Premi il tastole otterrai il valore del terzo lato. |  |
| Passaggio #6 Utilizza una variabile d'appoggio O per immagazzinare il valore del primo angolo [math](\\cos((A^2+C^2-B^2)/(2AC)))^-1=0[/math]
Premi il tasto 1 e otterrai l'ampiezza dell'angolo compreso tra i lati A e C. |  |
| Passaggio #7 Utilizza una variabile d'appoggio P per immagazzinare il valore del secondo angolo [math](\\cos((A^2+C^2-B^2)/(2AC)))^-1=p[/math]
Premi il tastole otterrai l'ampiezza dell'angolo compreso tra i lati B e C. | 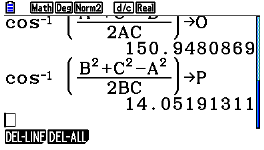 |
| Passaggio #8 Come prova dei calcoli svolti, somma i tre angoli P, O e [math] h\eta[/math] e devi ottenere 180°. |  |
Le stesse formule vengono rivalutate sulla base dei nuovi valori.


