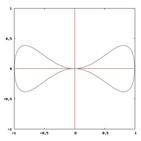
Curva a bifoglio
# Bifoglio.
# Equazione parametrica:
# x = (a+bt) / (1+t^2)^2
# y = tx
#
set terminal png medium size 480,480
set output "bifoglio.png"
set parametric
set size ratio 1
set zeroaxis ls 1
set xtics ("0" 0, "a=0.25" 0.25)
a = 0.25
set samples 400
plot (a+t)/(1+t**2)**2, t*((a+t)/(1+t**2)**2)
notitle with line lc "black" lw 2
set output
1' di lettura
5
/
5
(1)