Gnuplot è un programma che consente di tracciare grafici di funzioni o di dati a due o tre dimensioni. È gratuito e i sorgenti sono disponibili, ma non è open source in senso stretto poiché non è consentito diffonderne versioni modificate. Il software può essere utile per anche per gli studenti della scuola secondaria. Si ottengono grafici di funzioni, curve e superfici di ottima qualità. E' adatto anche per la computer art o math-art.
.
Introduzione
Esistono versioni di gnuplot per molte piattaforme, anche se gli ultimi rilasci vengono collaudati estensivamente solo su Unix/Linux, Windows e OSX.
Quale che sia la piattaforma, il programma è sempre a linea di comando.
Su Unix/Linux viene eseguito digitando gnuplot in una finestra xterm (o equivalenti); appare quindi il prompt "gnuplot> ", dopo il quale vanno digitati i comandi. Il programma può essere eseguito anche indicando il nome di un file di testo contenente una successione di comandi, che vengono eseguiti in sequenza. Si opera analogamente su OSX, eseguendo gnuplot dal Terminal, da suoi sostituti come iTerm, oppure da xterm.
Per Windows esiste un eseguibile wgnuplot.exe che apre una finestra dotata di menù; in questa viene però comunque proposta l'interfaccia a riga di comando con lo stesso prompt.
Il comando help propone un'estesa guida in linea, tanto estesa che non è facile orientarsi per chi si avvicini le prime volte al programma.
Speriamo che questa breve intriduzione aiuti ad acquisire quel minimo di familiarità necessario per poter poi sfruttare appieno, secondo necessità, la ricca messe di comandi e di opzioni.
.
Installazione
Molte distribuzioni Linux comprendono già gnuplot; se non risulta già disponibile, lo si può installare usando il package manager della propria distribuzione (rpm per RedHat, YaST per Suse, APT per Debian, ecc.). Chi desidera scaricare e compilare i sorgenti, può scegliere uno dei siti indicati nell'apposita pagina del sito ufficiale.
Dagli stessi siti si possono scaricare le versioni già compilate per Windows, riconoscibili per la presenza di "win" nel nome del file (ad esempio, gp422win32.zip da quest'elenco). Per l'installazione è sufficiente scompattare il file in una qualsiasi cartella. Su OSX si può installare il programma con Fink, usando il comando apt-get install gnuplot oppure l'interfaccia grafica FinkCommander, ma si possono anche scaricare e compilare i sorgenti come su Linux.
Lanciare dalla cartella Bin il file wgnuplot.exe. Può essere utile memorizzare la cartella in una qualsiasi cartella dell'hard disk e creare sul desktop un collegamento al file eseguibile.
.
Grafici bidimensionali
Appena eseguito il programma, viene proposto un prompt dal quale è subito possibile costruire grafici.
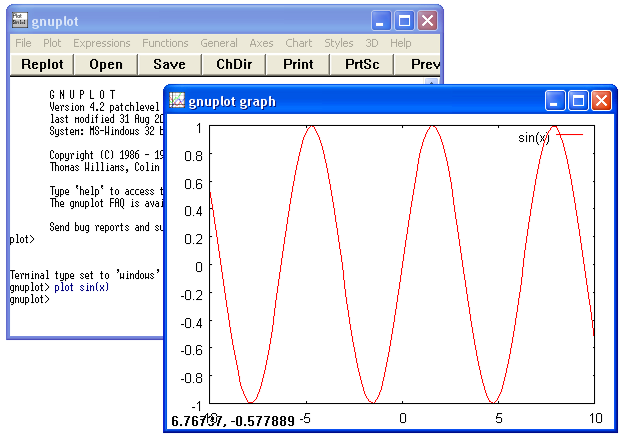
Ad esempio: gnuplot> plot sin(x) traccia il grafico della funzione seno.
L'insieme delle funzioni disponibili è molto ampio, tanto che preferiamo riviare al manuale, qui ne indichiamo solo qualcuna: abs(x), exp(x), log(x), sqrt(x), tan(x).
Sottolineamo, piuttosto, che è possibile definire nuove funzioni a partire da quelle disponibili (ne vedremo qualche esempio più avanti).
Il grafico che si ottiene viene prodotto adottando valori di default per un gran numero di opzioni (per vederle tutte, si può usare il comando show all). Ad esempio:
-
terminal: il dispositivo grafico di output; per default vale x11 su Linux (e su OSX se si usa gnuplot da xterm), windows su Windows, aqua su OSX (se si usano Terminal o iTerm);
-
xrange e yrange (e zrange per i grafici in 3D): il campo di variazione di x (variabile indipendente) e y (variabile dipendente, f(x)); vengono impostati automaticamente su valori "ragionevoli";
-
zeroaxis: se ON (per default è OFF) mostra gli assi coordinati;
-
title: il titolo del grafico, nullo per default, scritto sopra il box che lo racchiude.
Anche plot ha sue opzioni, che consentono di definire tipo, colore e spessore delle curve tracciate nel grafico. Va forse sottolineato che tra queste c'è un'opzione title diversa da quella appena menzionata. Per default, un comando come plot sin(x), oltre a tracciare il grafico della funzione seno, scrive "sin(x)" in alto a destra seguito da un segmento tracciato con le stesse opzioni usate per tracciare la curva. Questo è utile quando si tracciano più funzioni, ad esempio con il comando plot sin(x), cos(x): le curve verranno tracciate in modo diverso (per default, linee continue di colore diverso) e la legenda in alto a destra consente di individuarle.
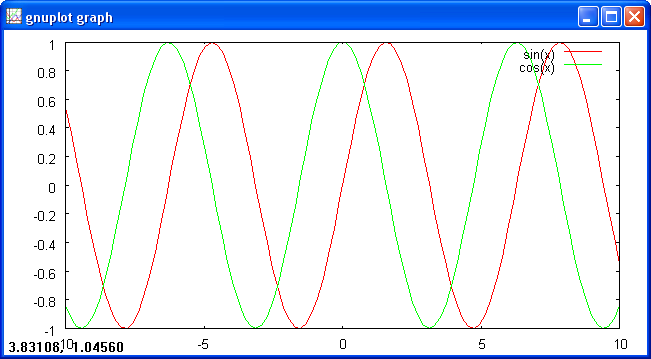
Si può assegnare un nome diverso alle singole curve indicandolo dopo ciascuna funzione (ad esempio: plot sin(x) title "seno", cos(x) title "coseno"), oppure non mostrarne alcuno scrivendo notitle.
In sostanza, set title imposta il titolo del grafico, che viene scritto per default sopra il grafico, plot
.
Coordinate cartesiane
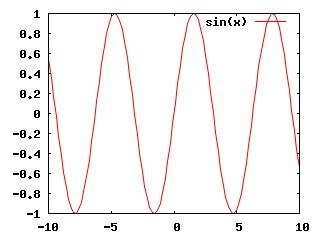
Il grafico della figura che segue è stato prodotto con il solo comando: plot sin(x)
Il grafico della figura che segue è stato prodotto con il comando: plot sin(x) title "seno", cos(x) title "coseno"
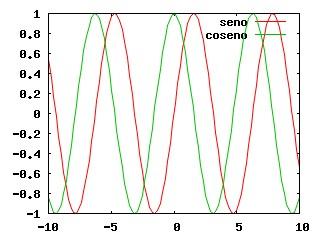
Il grafico della figura che segue è stato prodotto con i comandi:
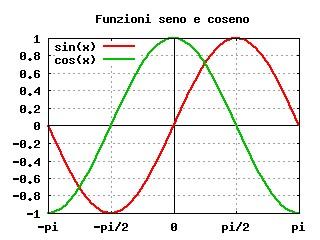set title "Funzioni seno e coseno"
set xrange[-pi:pi]
set xtics ("-pi" -pi, "-pi/2" -pi/2, "0" 0, "pi/2" pi/2, "pi" pi)
set zeroaxis lt rgb "black"
set zeroaxis lt 2
set grid
set key top left
plot sin(x) lw 2, cos(x) lw 2
Il primo imposta il titolo del grafico. Il secono imposta il campo di variazione della variabile indipendente da -π a π (la costante π si indica con "pi"; vedremo tra breve come scriverla meglio su un grafico), il successivo suddivide l'asse delle ascisse in intervalli larghi π/2.
I due comandi set zeroaxis tracciano gli assi delle ascisse e delle ordinate in nero e con un tratto continuo (per default, ovvero dando il comando senza opzioni, vengono tracciati con linee punteggiate).
Il comando set grid fa sì che venga tracciata una griglia di linee punteggiate secondo i "tic" (gli estremi degli intervalli) definiti sui due assi.
Il comando set key top left sposta la legenda in alto a sinistra, in modo che non si sovrapponga ai grafici delle funzioni. L'ultimo comando traccia i grafici del seno e del coseno, entrambi con una linea continua di spessore 2.
.
Coordinate polari
Il grafico della figura che segue è stato prodotto con i comandi: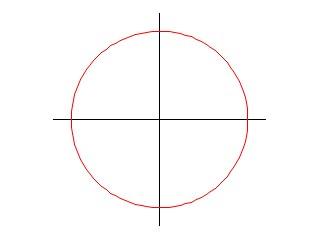
set polar
set xrange[-1.2:1.2]
set yrange[-1.2:1.2]
set size ratio 1
unset border
unset tics
set zeroaxis lt rgb "black"
set zeroaxis lt 2
plot 1 notitle
Il primo comando imposta le coordinate polari, i due successivi definiscono il campo di variazione delle variabili. Il comando set size ratio 1 fa sì che, quali che siano le dimensioni della finestra di output, i due assi coordinati abbiano la stessa scala. I due comandi unset eliminano sia il rettangolo che per default delimita il grafico (come negli esempi visti fin qui), sia i "tic" definiti lungo gli assi coordinati. I tre comandi finali sono analoghi ad altri già visti. Si può magari sottolineare che, avendo impostato le coordinate polari, per tracciare il cerchio è sufficiente indicarne il raggio (in questo caso, 1).
Il grafico della figura seguente è stato prodotto con i comandi:
set polar set trange[0:38]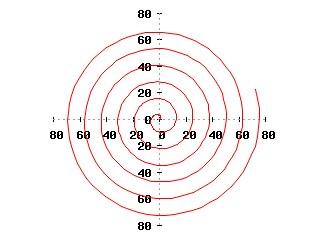
set size square
unset border
set zeroaxis
set xtics axis
set ytics axis
set samples 400
plot 2*t notitle
Una volta impostate le coordinate polari, la variabile indipendente viene chiamata t e si usa il comando set trange per impostarne il campo di variazione. set size square è identico al già visto set size ratio 1. L'opzione axis dei comandi che governano i "tic" fa sì che questi vengano tracciati sugli assi coordinati invece che sul rettangolo che delimita il grafico. Il comando set samples consente di aumentare la "risoluzione" del grafico, in modo da ottenere grafici più accurati (più simili a curve vere e proprie che a spezzate).
Nella figura seguente (adattata da http://gnuplot.sourceforge.net/demo_4.0/polar.html ) si usano due funzioni per comporre un'unica figura:
set polar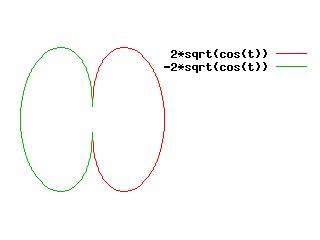
set size square
unset border
unset tics
set key outside
set samples 400
plot 2*sqrt(cos(t)),-2*sqrt(cos(t))
Il comando set key outside pone la legenda fuori del rettangolo che delimita la figura, anche se, avendo usato unset border, il rettangolo non viene disegnato.
.
Funzioni parametriche
Per usare funzioni parametriche si usa il comando set parametric, dopo il quale le funzioni vanno definite in termini della variabile t per disegni bidimensionali, delle variabili u, v per disegni tridimensionali
Una funzione parametrica bidimensionale va definita mediante una coppia di funzioni. Ad esempio, la retta di equazione
Le due funzioni di t vanno indicate nel seguente ordine: prima quella per x, poi quella per y. La figura che segue mostra il grafico di due rette per mettere in evidenza l'importanza dell'ordine con cui vengono indicate le due funzioni di t. È stata prodotta con i comandi: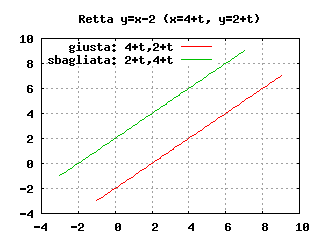
.
set parametric
set title "Retta y=x-2 (x=4+t, y=2+t)"
set grid
set key top left
plot 4+t,2+t title "giusta: 4+t,2+t", 2+t,4+t title "sbagliata: 2+t,4+t"
.
Come si vede, il comando plot 4+t,2+t produce il grafico della retta y=x-2, mentre plot 2+t,4+t produce il grafico di una retta traslata in alto (y=x+2).
.
La figura seguente mostra un cardioide. I comandi con i quali è stata ottenuta sono: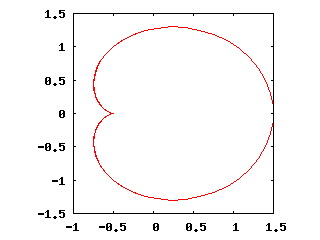 
.
set parametric
set size square
plot cos(t)+0.5*cos(2*t),sin(t)+0.5*sin(2*t)
notitle
.
.
.
.
La figura seguente, adattata da http://gnuplot.sourceforge.net/demo_4.0/param.html , mostra alcune sezioni coniche ottenute parametrizzando rispetto a t.
Sono state ottenute con i seguenti comandi: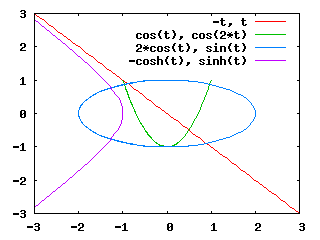 
.
set parametric
set xrange[-3:3]
set yrange[-3:3]
plot -t,t,cos(t),cos(2*t),2*cos(t),sin(t),-cosh(t),sinh(t)
.
.
.
.
.
Grafici tridimensionali
Produrre grafici tridimensionali è piuttosto semplice: basta usare splot (surface plot) invece di plot. Vi sono, tuttavia, interessanti differenze. Ad esempio, quando si usa il terminale di default (cioè lo schermo), le immagini sono "animabili", nel senso che cliccando col tasto sinistro del mouse e tenendolo premuto si può cambiare come si desidera la prospettiva.
Vi sono poi apposite opzioni per una resa migliore rispetto a quelle già viste. Quelle che più si distinguono sono quelle che consentono di colorare le superfici e di eliminare le linee nascoste. Vengono infatti spesso tracciate superfici, rese normalmente con griglie di linee (o punti) più o meno fitte, ed è possibile sia rappresentarle come vere e proprie superfici colorate, invece che tratteggiate, sia evitare la visualizzazione di porzioni di superfici che rimangono nascoste da altre.
Le tre figure che seguono sono adattate da http://gnuplot.sourceforge.net/demo_4.0/
La figura che segue è stata prodotta con i comandi: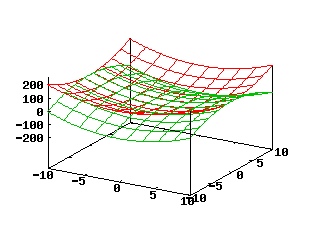 
.
set zrange[-200:250]
set ztics ("-200" -200, "-100" -100, "0" 0, "100" 100, "200" 200)
splot x**2+y**2 notitle, x**2-y**2 notitle
.
Si può notare che splot e plot si usano in modo molto simile, con l'ovvia differenza che le funzioni vengono espresse in termini delle due variabili x e y. Vi sono inoltre comandi come set zrange e set ztics per l'asse z.
Le superfici che rappresentano le due funzioni sono tracciate ciascuna con una griglia di linee e sono "trasparenti", nel senso che si vedono anche porzioni che resterebbero nascoste se le superfici fossero compatte.
.
Eliminazione delle linee nascoste
La figura che segue mostra un grafico tracciato con equazioni parametriche. Per ottenere il grafico è stato usato il comando set hidden3d che elimina le linee nascoste: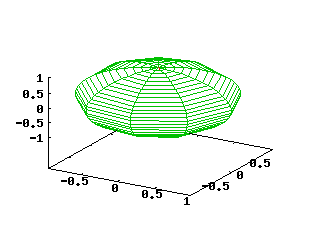
.
set parametric
set isosamples 30,10
set hidden3d
set xtics -1, .5, 1
set ytics -1, .5, 1
set ztics -1, .5, 1
set urange [ -1.57080 : 1.57080 ]
set vrange [ 0.00000 : 6.28319 ]
splot cos(u)*cos(v),cos(u)*sin(v),sin(u) notitle
Quando vengono tracciati grafici a due dimensioni, le curve sono in realtà linee spezzate che appaiono come curve vere e proprie tanto più quanto più si aumenta la risoluzione con il comando set samples.
I grafici a tre dimensioni vengono tracciati con segmenti che uniscono i punti di curve di livello (isoline); la risoluzione del grafico può essere aumentata in due direzioni: il primo numero dopo set isosamples governa la distanza tra le curve di livello, il secondo determina il numero dei punti che compongono le singole curve di livello. Si può dire che i due numeri regolano, rispettivamente, la risoluzione "verticale" e quella "orizzontale" del grafico (a spese del tempo richiesto per tracciarlo).
La figura di prima mostra anche un altro uso dei comandi set [x|y|z]tics: si può modificare l'intervallo dei "tic" indicando il primo, l'incremento e l'ultimo.
.
Colorazione delle superfici
La figura che segue mostra ancora un grafico tracciato con equazioni parametriche, ma viene usato il comando set pm3d (palette mapped 3d) per colorare le superfici: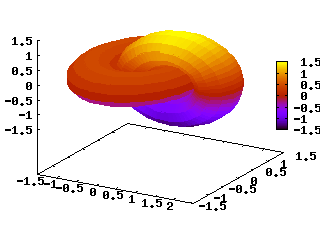
.
set parametric
set isosamples 50,20
set pm3d depthorder
set view 60, 30, 1.1, 1.33
unset key
set xtics -1.5, .5, 2.5
set ytics -1.5, .5, 1.5
set ztics -1.5, .5, 1.5
splot cos(u)+.5*cos(u)*cos(v),sin(u)+.5*sin(u)*cos(v),.5*sin(v) with pm3d,
1+cos(u)+.5*cos(u)*cos(v),.5*sin(v),sin(u)+.5*sin(u)*cos(v) with pm3d
Le diverse sfumature di colore rendono la distanza lungo l'asse z dal piano xy. Viene mostrata anche una colonna con la scala dei colori (può essere eliminata con unset colorbox).
Non si usa il comando set hidden3d, ma l'opzione depthorder di set pm3d; le superfici vengono colorate tenendo conto della loro profondità rispetto al punto di vista dell'osservatore e si ha, così, un effetto analogo a quello dell'eliminazione delle linee nascoste.
Il punto di vista dell'osservatore viene definito con il comando set view, che accetta quattro parametri: rotazione intorno all'asse x (da 0 a 180, 60 per default), rotazione intorno all'asse z (da 0 a 360, 30 per default), scala dell'intero grafico e scala dell'asse z (entrambi 1 per default).
Il comando usato per tracciare la figura precedente aumenta del 10% la dimensione dei due tori e li "allunga" del 30% in verticale. Normalmente i grafici vengono comunque tracciati come griglie di linee; per eliminarle ed ottenere solo superfici colorate si deve dare l'opzione with pm3d dopo ciascuna delle funzioni che si chiede a splot di tracciare.
.
Creazione di file
Finora abbiamo ipotizzato che i grafici venissero prodotti sul terminal di default, che è x11 per Unix/Linux, windows per Windows e aqua per OSX. Per creare un file sono sufficienti i comandi:
set terminal
...
set output
Con set terminal si sceglie il tipo di terminale e, se si desidera creare un file, il tipo di file, ad esempio jpeg o png. Possono essere indicate diverse opzioni, la più usata delle quali, size, determina le dimensioni del grafico. Con set output "
Le figure usate in questa introduzione sono state tutte create in questo modo, a volte come file jpeg, altre come file png. Per l'ultima figura, quella dei due tori, si è creato un file di testo "tori.gp" contenente i comandi:
set terminal png size 320, 240
set output "tori.png"
set parametric
set isosamples 50,20
set pm3d depthorder
set view 60, 30, 1.1, 1.33 unset key
set xtics -1.5, .5, 2.5
set ytics -1.5, .5, 1.5
set ztics -1.5, .5, 1.5
splot cos(u)+.5*cos(u)*cos(v),sin(u)+.5*sin(u)*cos(v),.5*sin(v) with pm3d,
1+cos(u)+.5*cos(u)*cos(v),.5*sin(v),sin(u)+.5*sin(u)*cos(v) with pm3d
set output
e si è poi eseguito gnuplot indicando il nome del file sulla riga comandi:
uplot ori.gp
.
Tes o \text{enhanced}
Sia quando si tracciano grafici sullo schermo, sia, e soprattut o, quando si creano file, può essere utile scrivere testi che abbiano un forma o \più ricco di quello s\\tandard. Ciò si ottie
e usando l'opzio
e enhanced quando si sceglie il dispositivo di output.
Il dispositivo \più flessibile è il terminal postscript, per usare il quale è buona norma definire, con set fontpath, la collocazio
e dei font
el proprio sistema.
La figura che segue è stata \\costruita
el modo seguente.
1. Per prima \\cosa si è crea o un file di tes o \text{gaussiana.gp} con i comandi:[img alt=\text{fig13.png} width=\text{500} height=\text{350}]https://cdn.skuola.
et/
ews_fo o/images/s ories/software/g
uplot/fig13.png[/img]
set fontpath \text{/usr/share/fonts/default/ghostscript}
set terminal postscript eps enhanced font \text{arial,28}
set output \text{gaussiana.eps}
set xrange [-5:5]
set yrange [0:.5]
set key spacing 1.3 e = exp(1)
plot 1/\sqrt{2 \cdot \pi} \cdot e \cdot \cdot (-x \cdot \cdot 2/2) title \text{(2{/Symbol p})^{(-1/2)}e^{-x^2/2}}
set output
2. Si può notare che,
ell'opzio
e title di plot si è indica o il \pi greco con \text{{/Symbol p}} e si è usa o l'accen o circonflesso, \text{^}, per gli espo
enti; si è poi crea o il file \text{gaussiana.eps} dalla riga comandi, con:
[/math]
3. Si è infine trasformato il file "gaussiana.eps" in un file di tipo png usando Ghostscript:
gs -dNOPAUSE -sDEVICE=png16 -sOutputFile=gaussiana.png -g500x350 -dBATCH gaussiana.eps
.
Conclusioni
In questa breve introduzione abbiamo cercato di dare un'idea delle potenzialità di gnuplot e dei comandi di uso più frequente. Speriamo che gli esempi proposti possano essere utili per chi voglia cominciare a creare i propri grafici, ma ciascuno di essi dovrebbe essere visto solo come una prima indicazione circa l'uso di comandi che, in realtà, hanno insiemi di opzioni molto più vasti di quanto qui illustrato.
Crediamo opportuno, quindi, rinviare sia al sito ufficiale, sia ad altri siti Internet; in particolare:
dalla pagina http://www.gnuplot.info/screenshots/index.html si accede ad una ricca messe di esempi;
la pagina http://www.gnuplot.info/docs/gnuplot.html contiene la documentazione completa di Gnuplot;
la pagina http://www.gnuplot.info/faq/faq.html contiene risposte alle domande più frequenti circa l'uso del programma;
la pagina http://t16web.lanl.gov/Kawano/gnuplot/index-e.html contiene moltissime informazioni utili, corredate da numerosi esempi.
