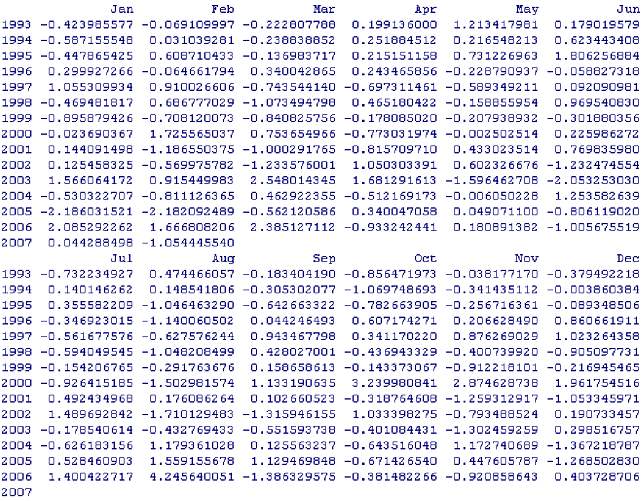
Per verificare che i residui si distribuiscano effettivamente secondo una variabile aleatoria normale, occorre preliminarmente individuare e rimuovere i valori anomali presenti. È preferibile operare sui residui standardizzati in quanto numeri puri:
> stand+ s=(var(x)^0.5)
+ z=(x-m)/s
+ return(z)}
Si crei il vettore dei residui standardizzati:
> res.stand> res.stand
e se ne tracci il grafico:
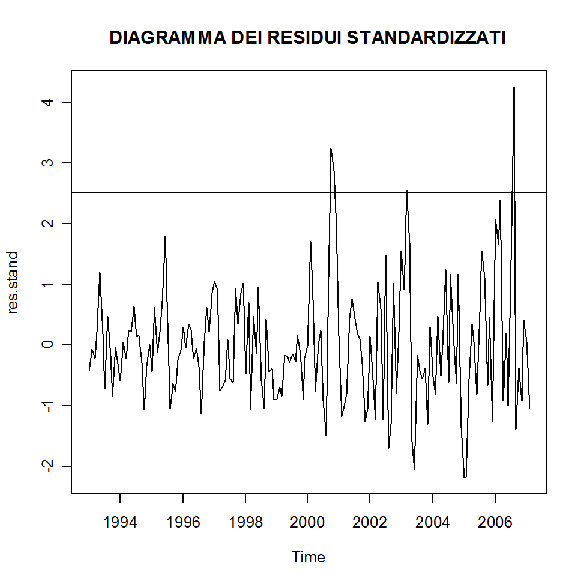
> plot(res.stand,main="DIAGRAMMA DEI RESIDUI STANDARDIZZATI")
> abline(h=2.5)
Dal diagramma emerge che solo due osservazioni risultano essere anomale poiché si trovano al di là della banda di confidenza del 99% ( banda compresa tra -2,5 e 2,5).
Si può ragionevolmente supporre che la causa risieda in fattori o eventi di natura episodica.Un modo abbastanza semplice ed intuitivo per verificare la normalità della distribuzione degli errori è quello di ricorrere ad un ausilio grafico:
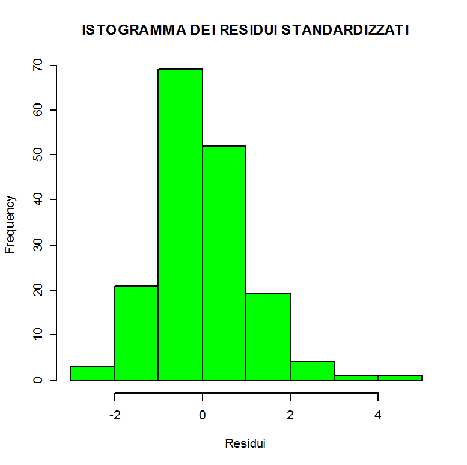
> hist(res.stand,main="ISTOGRAMMA DEI RESIDUI STANDARDIZZATI",xlab="Residui",col="green")
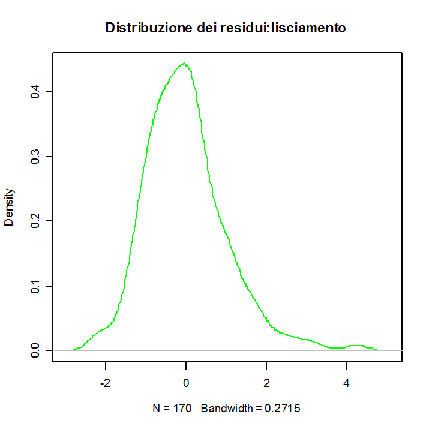
> plot(density(res.stand,kernel="gaussian"),main="Distribuzione dei residui:lisciamento",col="green")
Entrambi i grafici ci danno una buona indicazione per una probabile distribuzione normale dei residui. Per avere un risultato più affidabile bisogna effettuare ulteriori test, in particolare si ricorre al test di Wilk – Shapiro.