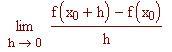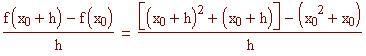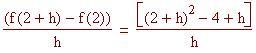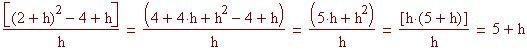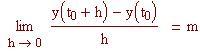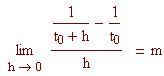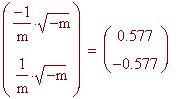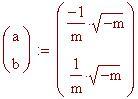Coefficiente angolare della retta tangente
In geometria piana, una retta si dice tangente a una circonferenza se interseca la circonferenza in un solo punto, secante se interseca la circonferenza in due punti, esterna se non ha alcun punto d'intersezione con la circonferenza. Per altri tipi di curve, una retta può intersecarle in un solo punto, ma non essere tangente. Se vogliamo applicare il concetto di tangente ad altre curve diverse dalla circonferenza abbiamo bisogno di una definizione matematica più generale.
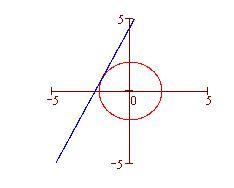
La retta blu è una tangente.
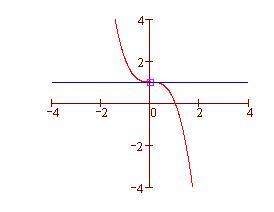
La retta blu è tangente?
Per definire il coefficiente angolare di una tangente usiamo il concetto di limite. Nel file precedente abbiamo definito la retta secante, che passa per due punti della curva. Ora definiamo la retta tangente in un singolo punto (x 0 , f(x 0 )) alla curva f(x) come la retta che passa per P 0 (x 0 , f(x 0 )) il cui coefficiente angolare è il limite, per h tendente a zero, dei coefficienti angolari delle secanti che passano per i punti P 0 (x 0 , f(x 0 )) e P(x 0 +h, f(x 0 +h )).
Coefficiente angolare della retta tangente nel punto P 0 (x 0 , f(x 0 )) alla curva f(x):
Troviamo il coefficiente angolare della tangente alla curva nel punto (2, 6).
Funzione:
ascissa del punto P 0 :
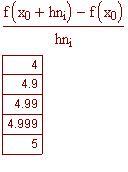
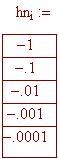
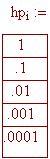
Valutiamo l'espressione del limite per piccoli valori di h, sia positivi che negativi.
Osservate a quale numero si avvicinano i valori sulle colonne di destra per valori di h tendenti a zero
Per confermare che il coefficiente angolare della tangente è 5, sostituiamo la definizione di f(x) nell'espressione del limite ed espandiamo.
Poiché sostituiamo questo valore nell'espressione .
Per sostituzione si ottiene:
Quindi si espande:
Finalmente valutiamo il risultato quando h si avvicina a zero:
otteniamo
Troviamo il punto sulla curva in cui il coefficiente angolare della tangente è –0.3 . Rappresentiamo graficamente y(t), la retta tangente e la perpendicolare (o normale).
Provate ad assegnare ad m altri valori. Poi guardate, alla fine della pagina, l'animazione cliccando sul relativo grafico!
Il coefficiente angolare della tangente in (t 0 , y(t 0 )) è:
Sostituiamo la definizione di y(t) nell'espressione del limite, selezioniamo t 0 e e risolviamo rispetto alla variabile t:
ha soluzioni
Poiché ci sono 2 soluzioni, esistono due punti, due rette tangenti e due normali.
Il coefficiente angolare m perp di rette perpendicolari
soddisfa la relazione m m perp = –1, così:
Equazioni delle tangenti:
Equazioni delle normali:
Per vedere cosa succede assegnando ad m altri valori cliccate sul grafico seguente!
tangenti
e normali
variabili
animazione
a cura di
Carlo Elce