Parabola: definizione, equazione e risoluzione di problemi

In questo appunto di Geometria verrà prima introdotta la definizione di Parabola con relativa equazione per la rappresentazione nel piano cartesiano, per poi essere utilizzata nella risoluzione di problemi di geometria analitica.

Definizione ed equazione della Parabola

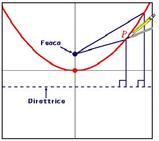
Si definisce Parabola il luogo geometrico dei punti del piano cartesiano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice; quest’ultima è sempre perpendicolare all’asse di simmetria della parabola, che può essere verticale o orizzontale.
I punti di coordinate (x,y) appartenenti alla parabola con asse di simmetria parallelo all’asse y, devono soddisfare la seguente equazione:

Viceversa, quando l’asse di simmetria è parallelo all’asse x, l’equazione della parabola diventa:

In pratica abbiamo sostituito i termini della

con quelli della .
Ad ogni modo, il punto d’incontro tra l’asse di simmetria e la parabola, prende il nome di vertice della parabola.
Quindi, riassumendo, gli elementi caratteristici di una parabola sono:

• vertice
  [math]V[/math]
  ;
• asse di simmetria
  [math] s[/math]
  ;
• fuoco
  [math]F[/math]
  ;
• direttrice
  [math]d[/math]
  .

Ovviamente, così come abbiamo visto nel caso dell’equazione della circonferenza, le coordinate o le equazioni di questi elementi possono essere estrapolati dall’equazione della parabola o, viceversa, dati questi elementi si può ottenere l’equazione della parabola corrispondente.
In particolare, se l’asse di simmetria è parallelo all’asse Y, allora avremo:

• equazione della parabola:
  [math]y=a x^2+b x+ c [/math]
• vertice:
  [math] V=(-\frac{b}{2a};-\frac{\Delta}{4a}) [/math]
• fuoco:
  [math] F=(-\frac{b}{2a};-\frac{1-\Delta}{4a}) [/math]
• asse di simmetria:
  [math] x=-\frac{b}{2a} [/math]
• direttrice:
  [math] y=-\frac{1+\Delta}{4a}[/math]

N.B. l’equazione della parabola è un’equazione di secondo grado in x, quando l’asse di simmetria è parallelo all’asse Y, in y quando l’asse di simmetria è parallelo all’asse X. Di conseguenza, ricordando come si risolvono le equazioni di secondo grado il sarà pari a:
.
Viceversa, se l’asse di simmetria è parallelo all’asse X avremo:

• equazione della parabola:
  [math]x=a y^2+b y+ c [/math]
• vertice:
  [math] V=(\frac{\Delta}{4a};-\frac{b}{2a}) [/math]
• fuoco:
  [math] F=(-\frac{1-\Delta}{4a};-\frac{b}{2a} ) [/math]
• asse di simmetria:
  [math] y=-\frac{b}{2a} [/math]
• direttrice:
  [math] x=-\frac{1+\Delta}{4a}[/math]

Dopo questa breve introduzione possiamo passare al prossimo paragrafo dove è presente un’applicazione di quanto detto finora per la risoluzione di alcuni esercizi.

Applicazione dell’equazione della Parabola

Dopo aver compreso meglio l’equazione della parabola e le possibili varianti nel caso di asse parallelo all’asse Y o X, passiamo adesso alla risoluzione di alcuni esercizi.
In particolare, uno degli esercizi più proposti relativi a quest’ambito è quello in cui si vuole trovare l’equazione della parabola passante per tre punti; vediamo un esempio.
Consegna:
Scrivere l'equazione della parabola, con asse parallelo all'asse , passante per i punti A,B e C, di coordinate rispettivamente:
.
Svolgimento:
Intanto rappresentiamo in un diagramma cartesiano i punti di coordinate rispettivamente .
Dopodiché scriviamo l'equazione di una parabola generica con l'asse parallelo rispetto all'asse , ovvero:

E chiamiamo

questa equazione.

N.B. In pratica dobbiamo trovare i valori di dell’equazione della parabola. Si tratta di un’equazione in tre incognite, infatti ci vengono forniti i valori delle coordinate di 3 punti. Con due punti non avremmo mai potuto risolvere il sistema perché il numero delle incognite deve essere sempre inferiore o pari al numero di dati forniti.
Torniamo al nostro problema.
Scritta l’equazione generica della parabola, a questo punto dobbiamo imporre che i punti appartengano alla parabola, cioè che le coordinate

dei punti soddisfino l'equazione della parabola.

Questa operazione si fa semplicemente sostituendo a e a le coordinate dei tre punti dati. In particolare, avremo che:

• sostituiamo
  [math]A(-1;0) \ in \ f(x,y) \Rightarrow c=-1[/math]
  ;
• sostituiamo
  [math]B(2;1) \ in \ f(x,y) \Rightarrow a+b+c=2[/math]
  ;
• sostituiamo
  [math]C(5;-2) \ in \ f(x,y) \Rightarrow 4a-2b+c=5[/math]
  .

Mettiamo ora a sistema le tre equazioni; come detto precedentemente abbiamo un sistema di tre equazioni in tre incognite, quindi lo possiamo risolvere semplicemente per sostituzione.
N.B. Possiamo risolvere il sistema in qualunque altro modo abbiamo visto nell’appunto di metodi di risoluzione di sistemi lineari, la scelta è totalmente arbitraria perché la soluzione non cambia. In questo caso abbiamo scelto la risoluzione per sostituzione, ma potete provare ad utilizzare un altro metodo per esercitazione.
Quindi utilizzando il metodo di risoluzione per sostituzione otteniamo:

;

;

;

;

;

;

Bene, ottenuti i valori delle incognite

possiamo finalmente scrivere l'equazione della parabola passante per i punti , ovvero:

A questo punto potete esercitarvi provando a scrivere l’equazione della parabola per altri tre punti, ricordando che non sempre si può ottenere una soluzione accettabile.
Per i più curiosi nel prossimo sono riportati dei link di approfondimento sull’argomento.

Approfondimenti sull’equazione della parabola

Per ulteriori approfondimenti sull’equazione della parabola potere consultare i seguenti link:

• parabola:elementi e la sua equazione
• equazione della parabola