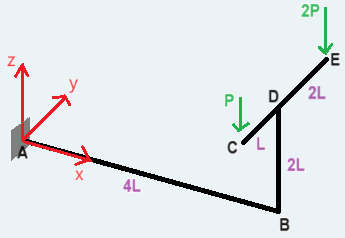
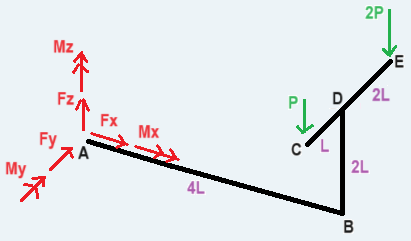
Per il calcolo delle reazioni vincolari nell'incastro ho impostato le 6 equazioni cardinali secondo i versi riportati nella figura seguente (figura a sx):

Quindi impostando l'equilibrio rispettivamente lungo gli assi $x,y,z$ ottengo:
\[ X_A=0; \: \: Y_A=0; \: \: Z_A=P+2P=3P \]
Per l'equilibrio dei momenti prendo come polo A e sfrutto la definizione stessa di momento. Analizziamo prima il vettor momento dato dalla forza P. Il vettore che congiunge A con C avrà componenti:
$ \vec{AC}=(4l,-l,2l)$. Mentre il vettore della forza P sarà $\vec{P}=(0,0,P)$. Quindi:
\[ \vec{AC} \times \vec{P}=det \begin{bmatrix} i & j & k \\ 4l & -l & 2l \\ 0 & 0 & P
\end{bmatrix} =(-Pl,-4Pl,0) \]
Definendo con la stessa logica $\vec{AE}=(4l,2l,2l)$ e $\vec{2P}=(0,0,2P)$, moltiplicandoli vettorialmente si ottiene:
\[ \vec{AE} \times \vec{2P}=det \begin{bmatrix} i & j & k \\ 4l & 2l & 2l \\ 0 & 0 & 2P \end{bmatrix}=(4Pl,-8Pl,0) \]
Le equazioni per la rotazione rispettivamente attorno agli assi x,y,z diventano:
\begin{cases}
-Pl+M_x+4Pl=0 \\
M_y-4Pl-8Pl=0 \\
M_z=0
\end{cases}
Che conducono quindi alle reazioni:
\begin{cases}
X_A=0 \\ Y_A=0 \\ Z_A=3P \\ M_x=-3Pl \\ M_y=12Pl \\ M_z=0
\end{cases}
Per quanto riguarda le caratteristiche lungo il tratto AB, con riferimento alla figura a destra, si possono scrivere le seguenti equazioni per gli equilibri di traslazione.
\[ N=0; \: \: T_z=0; \: \: T_y=0 \]
Mentre definendo il vettore che congiunge A con la sezione tagliata (quest'ultima sarà il polo) si ottiene $\vec{S}=(-s,0,0)$. L'unica forza che dà momento è la reazione $Z_A=3P$. Quindi:
\[
\vec{S} \times (0,0,3P)=(0,+3Ps,0) \]
Quindi si ottengono:
\[ \begin{cases}
M_x-3Pl=0 \\ M_y+12Pl+3Ps=0 \\ M_z=0
\end{cases} \]
Quindi le uniche caratterische non nulle sono il taglio lungo $z$ che è costantemente $T_z=3P$ e il momento $M_y=-3Ps-12Pl$ che ha andamento lineare lungo $AB$.
Può andare? Intanto vediamo se ciò che ho fatto per il tratto AB è corretto, poi proverò a scrivere le equazioni pure per BD!
Grazie per aver letto fin qua :]