Circonferenza tangente a punto

[sarrus89S]

Qualcuno di voi sa aiutarmi per la rappresentazione della circonferenza?
Il quesito è questo :
Determinare la retta r passante per il punto A(1,-1) e parallela alla retta s :2x -y=1 . Rappresentare una circonferenza che sia tangente a r nel Punto A

utilizzando la formula mi trovo la retta r : y= 2x-3

[bobus]

Potresti trovare la retta perpendicolare a r nel punto A, poi su questa retta trovi il punto che dista da r quanto il raggio della circonferenza, visto che non è specificato puoi prendere 1 come distanza. Probabilmente c'è un modo più rapido e semplice, non sono molto esperto

[teorema55]

E' chiaro che manca un dato, oppure le circonferenze tangenti in A sono infinite, tutte con il centro (come correttamente già detto) sulla retta perpendicolare alle prime due passante per A. In tal caso, l'equazione della circonferenza conterrà un paramento in funzione del suo raggio.

[Seneca]

L'esercizio sembra un po' strano, ma d'altronde è richiesta "una" circonferenza (tra quelle che soddisfano le condizioni). Scritto così non mi sembra manchi alcun dato. Comunque farei come suggerito da bobus.

[orsoulx]

Probabilmente e stranamente la via più rapida consiste nello scrivere tutte le circonferenze soddisfacenti le condizioni, per indicarne poi una sola. Il fascio avente per sostegno le due circonferenze degeneri si scrive immediatamente:
$ (x-1)^2+(y+1)^2+\lambda(2x-y-1)=0 $
NB Ho utilizzato la retta s invece della r, l'equazione corretta sbagliata del fascio è
$ (x-1)^2+(y+1)^2+\lambda(2x-y+3)=0 $
NB2 Mi dicono che occorra anche scrivere esattamente le equazioni delle rette, e allora:
$ (x-1)^2+(y+1)^2+\lambda(2x-y-3)=0 $
Grazie a teorema55 ho scoperto l'errore gli errori.

Ciao

[teorema55]

Dici bene, Beppe.

Il problema è simmetrico rispetto alla

$y=2x-3$

quindi per ogni dato raggio le soluzioni sono 2...........

Se comunque si tratta di sceglierne una, basta assegnare a $ \lambda$ un valore arbitrario, per esempio

$\lambda=-1$

e si ottiene

$x^2 +y^2 +2y+1=0$

Per inciso, con

$\lambda=1$

la circonferenza non esiste, mentre, con

$\lambda=0$

degenera nel punto

$A(1, -1)$ ...................

................come sempre, correttezza dei calcoli supponendo.



EDIT: ah, monello, da te non me lo sarei aspettato................

[orsoulx]

Dici bene

Dico male, anzi malissimo!
Non è possibile che ci siano altre circonferenze 'strane' nel fascio (se scritto correttamente): ho usato la retta s invece della r.
Vado a correggere.
Ciao

[teorema55]

Sono io che avrei dovuto controllare i calcoli (mai fidarsi.........) ed ora che l'ho fatto temo che abbia ciccato di nuovo, amico mio. Secondo me la versione corretta per l'insieme di circonferenze è

$(x-1)^2 +(y+1)^2 +\lambda(2x-y-3)=0$

che infatti passa per $A(1,-1)$

Portata in forma esplicita ( $x^2 +y^2 +ax+by+c=0$ ) è

$x^2 +y^2 +2(\lambda -1)x-(2-\lambda)y +(2-3\lambda)=0$

Per avere il centro sulla

$y=-1/2x-1/2$

(la perpendicolare per $A(1,-1)$ alla $y=2x-3$)

questo deve avere coordinate $C(x_c,(-(x_c)/2 - 1/2))$

e il raggio deve essere la distanza tra $C$ ed $A$, cioè

$r=\sqrt((x_c -1)^2 + (1/2 -x/2)^2)$

che, dopo passaggi, è

$r=(\sqrt5(1-x_c))/2$

Ma il raggio è anche

$r=\sqrt(a^2 /4 + b^2 /4 -c)$

che, dopo passaggi,è

$r=(\sqrt5)/2 \lambda$

Uguagliando:

$(\sqrt5(1-x_c))/2=(\sqrt5)/2 \lambda$

otteniamo

$\lambda=1-x_c$

Da notare che, per ogni soluzione con la circonferenza dalla parte "sinistra" della retta $y=2x-3$, ce n'è un'altra simmetrica a questa rispetto la retta stessa, dalla sua parte "destra"

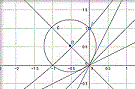
L'immagine rappresenta (a destra) la circonferenza

$x^2 +y^2 -4x+3y+5=0$

che, come si vede facilmente, si ottiene per

$\lambda=-1$

Questa ha centro

$C(2, -3/2)$

e raggio

$r=(\sqrt5)/4$

e la sua simmetrica sulla sinistra.

Si potrebbe calcolarne l'equazione con le formule della simmetria, ma data l'ora la cosa non mi passa neppure per l'anticamera del cervello, con buona pace di Alex.



Sempre salvo errori od omissioni

Buona notte.

Marco

[orsoulx]

temo che abbia ciccato

Poffarbacco! Hai ragione da vendere (attualmente è quotata 313 euro al milligrammo); bene han fatto a sbattermi fuori dalla scuola, con la scusa che ci avevo lavorato troppo.
Invece di passeggiare per i monti andrò ad emendare la prima correzione, grazie!

Si potrebbe calcolarne l'equazione con le formule della simmetria

O, più rapidamente, basta invertire il segno a $ \lambda $.
Ciao

[teorema55]

Se mi consenti, Beppe, suggerirei la prima soluzione (la montagna), ma........................okkio agli orsi! (Non so se......)

Ciao, buona passeggiata!