Quasi quadrato

[axpgn]

Determinare quanto vale l'area nera in figura:




Gli archi circolari interni hanno i centri sul bordo.


Cordialmente, Alex

[sellacollesella]

Testo nascosto, fai click qui per vederlo

Se \(r>0\) è il raggio del cerchio esterno, allora l'area nera dovrebbe essere \(A = 2\left(1-\sqrt{3}+\frac{\pi}{3}\right)r^2\). D'altro canto non sono riuscito a trovare un modo elementare, specie quella radice di tre non so farla saltar fuori. Ci penserò su con calma, ora meglio che pranzo se non voglio rischiare che mi sloggino!

[mgrau]

Testo nascosto, fai click qui per vederlo

Non è particolarmente elegante, ma si può trovare l'area della parte gialla, che è 1/8 del quasi quadrato.
Prendendo il raggio = 1, e come origine il punto in basso, l'arco superiore ha equazione $x^2 + y^2 = 2$, la linea obliqua è $ x = y - 1$, il vertice destro ha $x = sqrt(13)/4 - 1/2$ (se non ho sbagliato i conti) per cui si deve integrare $sqrt(x^2 - 2)$ fra zero e $sqrt(13)/4$, e poi sottrarre il trapezio verde.
(i calcoli effettivi però me li risparmio... )

[sellacollesella]

Testo nascosto, fai click qui per vederlo

Dopo aver pranzato, digerito e poltrito, il massimo che sono riuscito a fare è quanto segue:



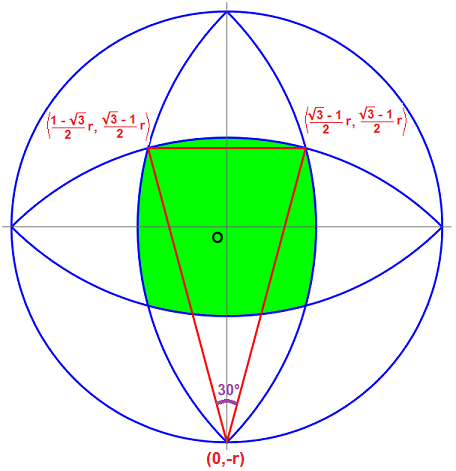
dove, una volta determinate le coordinate dei punti d'intersezione rossi e determinato l'angolo viola:
\[
A = 4\left(A_q + A_s - A_t\right) = 4\left[\left(\frac{\sqrt{3}-1}{2}r\right)^2 + \frac{1}{2}\,\frac{\pi}{6}\left(\sqrt{2}\,r\right)^2 - \frac{1}{2}\left(\sqrt{3}-1\right)r\left(r+\frac{\sqrt{3}-1}{2}r\right)\right]
\] che semplificata porta a quanto scritto qualche ora fa:
\[
A = 2\left(1-\sqrt{3}+\frac{\pi}{3}\right)r^2\,.
\] Mi turba l'aver risolto delle equazioni per trovare i punti d'intersezione ma non mi viene in mente altro.

[axpgn]

@sellacollesella
La formula finale è giusta

Ci sarebbero però un po' di passaggi da aggiungere

Testo nascosto, fai click qui per vederlo

Dalla definizione delle curve alla determinazione dell'angolo e dei punti di intersezione e alla specificazione del significato delle varie $A$.

Comunque ci sono strade meno impervie (come quella di mgrau per esempio)

@mgrau
L'idea è giusta ed è originale il suo svolgimento

Testo nascosto, fai click qui per vederlo

Però i conti vanno fatti (anche perché potrebbero essere sbagliati ) ed inoltre andrebbe poi generalizzato il tutto.

Cordialmente, Alex