[C] Compilatore e divisione

[utente__medio]

Ciao, personalmente non conosco il linguaggio assembly, ma per caso da una discussione è emerso che il compilatore per effettuare la divisione intera $D/18$ effettuasse il prodotto tra $D$ e il numero $954437177$, per poi eseguire uno shift a destra di $34$ posizioni.

Dal momento che la cosa mi incuriosiva, ho deciso di rifletterci un po' su, e la prima cosa che mi è venuta in mente per "trasformare" una divisione in una moltiplicazione è quella di moltiplicare il dividendo per l'inverso del divisore:

$D/18=1/2(D/9)=1/2(D*1/9)$

Essendo $9=(1001)_2$ ho svolto la divisione $1/9$ in binario



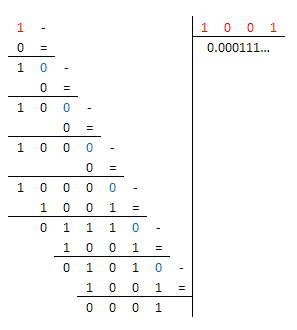
Dal momento che $1/9$ non può essere rappresentato in binario in modo esatto, ho pensato di approssimare la parte dopo la virgola in 32 bit (in modo che, ipotizzando che anche $D$ sia un intero a 32 bit, il loro prodotto possa essere espresso attraverso una variabile intera a 64 bit):

$1/9=1/(1001)_2=(0.bar(000111))_2\approx(0.000|11100011100011100011100011100011|)_2=$

$=(11100011100011100011100011100011)_2/2^(32+3)$

In definitiva quindi ottengo che la parte intera della suddetta divisione può essere calcolata come:

$[D/18]=[1/2(D*(0.bar(000111))_2)]=D*(11100011100011100011100011100011)_2$ \(\gg(32+3+1)\)

E' evidente che i $(11100011100011100011100011100011)_2=(3817748707)_(10)$ e $36$ ottenuti siano diversi dai $954437177$ e $34$ utilizzati dal compilatore, anche se utilizzando per l'approssimazione 30 bit e non 32 i numeri tornano "quasi" del tutto:

$D*((11100011100011100011100011100011)_2$ \(\gg2)\gg34=\)

\(=D*954437176\gg34\)

"Quasi" nel senso che il secondo fattore è più piccolo di un'unità rispetto a quello utilizzato dal compilatore.

-----------------------------------------------------------------------------------------------------------------------

In generale avremo quindi che

$[D/d]=D*q$ \(\gg\) $n$

con $q$ e $n$ che sono funzione di $d$.

Ovviamente affinché questo metodo sia performante i valori di $q$ e $n$ devono essere già noti; nel mio caso ho posto d_max = 100000 e ho utilizzato gli array v_q e v_n per contenere rispettivamente i valori di $q$ e $n$ calcolati (dalla funzione fun() ) per valori di $d$ appartenenti all'intervallo $[1;100000]$. Quindi per esempio per accedere ai valori di $q$ e $n$ per $d = 41$ basterà accedere rispettivamente agli elementi v_q[41] e v_n[41].

Per testare il tutto ho disabilitato le ottimizzazioni del compilatore (affinché non venissero ignorati i cicli) e ho misurato i tempi necessari a calcolare N volte una stessa divisione in diversi scenari:

- NATIVA: si riferisce alla divisione nativa del compilatore;
- OTTIMIZZATA CON ARRAY: si riferisce alla versione da me implementata con i valori di $q$ e $n$ prelevati rispettivamente dagli array v_q e v_n. Inoltre non ho utilizzato la funzione optimized_division() per velocizzare il tutto evitando le varie chiamate a funzione (visto che la parola chiave inline non sembra fare effetto);
- OTTIMIZZATA SENZA ARRAY: come sopra, ma i valori di $q$ e $n$ sono stati estratti dai due array per risparmiare sui tempi di accesso agli array.

Un altro test sulla velocità l'ho fatto misurando i tempi necessari a calcolare N divisioni in cui il divisore è dato da rand() + 1 (che nel mio caso va bene essendo RAND_MAX < d_max ).

Infine ho eseguito un test simile al precedente, ma questo volta non per calcolare i tempi, ma per valutare se la divisione nativa e la divisione da me implementata restituissero sempre gli stessi risultati.

Di seguito riporto il codice e l'output che ottengo lanciandolo:

Codice:

#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#include <time.h>

#define MAX_d 100000

uint32_t v_q[MAX_d + 1];
uint32_t v_n[MAX_d + 1];

void fun(const uint32_t max_d)
{
    for(uint32_t d = 2; d <= max_d; ++d)
    {
        uint32_t D = 1;
        uint32_t d_2 = d;
        uint32_t q = 0;
        uint8_t n = 0;
        for(; !(D & d_2); ++n, d_2 >>= 1);
        if(d == d_2)
        {
            for(; D < d_2; ++n, D <<= 1);
            for(uint8_t i = 0; i < 32; ++i)
            {
                q <<= 1;
                if(D > d_2)
                {
                    q |= 1;
                    D -= d_2;
                }
                D <<= 1;
            }
            v_q[d] = q;
            v_n[d] = n;
        }
        else
        {
            v_q[d] = v_q[d_2];
            v_n[d] = v_n[d_2] + n;
        }
    }
}

uint32_t optimized_division(const uint32_t D, const uint32_t d)
{
    if(d < D)
    {
        return v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d];
    }
    return d == D ? 1 : 0;
}

int main()
{
    uint32_t D = 941787252;
    uint32_t d = 36248; // <= MAX_d

    fun(MAX_d);
    printf("OK\n\n");

    uint32_t N = 50000000;
    srand(time(0));
    clock_t begin;
    clock_t end;

    begin = clock();
    for(uint32_t i = 0; i < N; ++i)
    {
        D / d;
    }
    end = clock();
    printf("%ux [ %u / %u = %u ] IN %fs (NATIVA)\n", N, D, d, D / d, (double)(end - begin) / CLOCKS_PER_SEC);

    begin = clock();
    for(uint32_t q = v_q[d], n = v_n[d], i = 0; i < N; ++i)
    {
        d < D ? (q ? (uint64_t)D * q >> 31 + n : D >> n) : (d == D ? 1 : 0);
    }
    end = clock();
    printf("%ux [ %u / %u = %u ] IN %fs (OTTIMIZZATA SENZA ARRAY)\n", N, D, d, d < D ? (v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d]) : (d == D ? 1 : 0), (double)(end - begin) / CLOCKS_PER_SEC);

    begin = clock();
    for(uint32_t i = 0; i < N; ++i)
    {
        d < D ? (v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d]) : (d == D ? 1 : 0);
    }
    end = clock();
    printf("%ux [ %u / %u = %u ] IN %fs (OTTIMIZZATA CON ARRAY)\n", N, D, d, d < D ? (v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d]) : (d == D ? 1 : 0), (double)(end - begin) / CLOCKS_PER_SEC);

    begin = clock();
    for(uint32_t i = 0; i < N; ++i)
    {
        D / (rand() + 1);
    }
    end = clock();
    printf("\n%ux [ %u / (rand() + 1) ] IN %fs (NATIVA)\n", N, D, (double)(end - begin) / CLOCKS_PER_SEC);

    begin = clock();
    for(uint32_t i = 0; i < N; ++i)
    {
        d = rand() + 1;
        d < D ? (v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d]) : (d == D ? 1 : 0);
    }
    end = clock();
    printf("%ux [ %u / (rand() + 1) ] IN %fs (OTTIMIZZATA CON ARRAY)\n", N, D, (double)(end - begin) / CLOCKS_PER_SEC);

    printf("\n------");
    for(uint32_t cont = 0, i = 0; i < N && cont < 5; ++i)
    {
        d = rand() + 1;
        if(D / d != optimized_division(D, d))
        {
            ++cont;
            printf("\n%u / %u = %u (NATIVA)", D, d, D / d);
            printf("\n%u / %u = %u (OTTIMIZZATA)\n", D, d, optimized_division(D, d));
        }
    }
    printf("------\n");
}

Codice:

OK

50000000x [ 941787252 / 36248 = 25981 ] IN 0.123000s (NATIVA)
50000000x [ 941787252 / 36248 = 25981 ] IN 0.119000s (OTTIMIZZATA SENZA ARRAY)
50000000x [ 941787252 / 36248 = 25981 ] IN 0.137000s (OTTIMIZZATA CON ARRAY)

50000000x [ 941787252 / (rand() + 1) ] IN 0.732000s (NATIVA)
50000000x [ 941787252 / (rand() + 1) ] IN 0.766000s (OTTIMIZZATA CON ARRAY)

------
941787252 / 84 = 11211753 (NATIVA)
941787252 / 84 = 11211752 (OTTIMIZZATA)

941787252 / 294 = 3203358 (NATIVA)
941787252 / 294 = 3203357 (OTTIMIZZATA)

941787252 / 252 = 3737251 (NATIVA)
941787252 / 252 = 3737250 (OTTIMIZZATA)

941787252 / 14 = 67270518 (NATIVA)
941787252 / 14 = 67270517 (OTTIMIZZATA)

941787252 / 3 = 313929084 (NATIVA)
941787252 / 3 = 313929083 (OTTIMIZZATA)
------

Process returned 0 (0x0)   execution time : 1.911 s
Press any key to continue.

A questo punto le questioni sono fondamentalmente due:

- ritenete che il compilatore utilizzi per la divisione intera un approccio simile a quello da me implementato?
Dai primi due test si evince relativamente ai tempi che OTTIMIZZATA CON ARRAY > NATIVA > OTTIMIZZATA SENZA ARRAY, il che mi fa pensare che il compilatore prelevi comunque i coefficienti da qualche parte, ma che questo prelievo sia più veloce rispetto a quello fatto dagli array globali v_q e v_n. Concordate sul fatto che anche il compilatore deve avere già a disposizione da qualche parte questi valori? E in tal caso dove e come ci accede?

- Dal terzo test si osserva che in alcuni casi (ossia per alcuni valori di $d$), la divisione da me implementata restituisce valori che sono più piccoli di un'unità rispetto al risultato reale. Come già ipotizzato in precedenza deve esserci qualche particolare che mi sfugge e di cui non ho tenuto conto nella fase di approssimazione; infatti se aumento i valori di $q$ di un'unità, i test fatti mi restituiscono sempre il risultato corretto. Come mai?

[apatriarca]

La divisione è in generale una operazione più lenta rispetto al prodotto. Per esempio, guardando nella tabella fornita da Agner Fog, troviamo che DIV ha una latenza di 10-12 cicli. La moltiplicazione su 32 o 64 bit (MUL) ha invece una latenza di soli 3 cicli e lo shift destro (SHR) ha una latenza di 1 ciclo. Quindi, nel caso in cui sia possibile calcolare direttamente l'inverso durante la compilazione, è conveniente fare uso di questo trucco. Nota che se avessi avuto una potenza di \(2\) si poteva convertire tutto in uno shift che era ancora più veloce.

[utente__medio]

Grazie per la risposta, ma quello che chiedevo era qualcosa di un po' più specifico:

A questo punto le questioni sono fondamentalmente due:

- ritenete che il compilatore utilizzi per la divisione intera un approccio simile a quello da me implementato?
Dai primi due test si evince relativamente ai tempi che OTTIMIZZATA CON ARRAY > NATIVA > OTTIMIZZATA SENZA ARRAY, il che mi fa pensare che il compilatore prelevi comunque i coefficienti da qualche parte, ma che questo prelievo sia più veloce rispetto a quello fatto dagli array globali v_q e v_n. Concordate sul fatto che anche il compilatore deve avere già a disposizione da qualche parte questi valori? E in tal caso dove e come ci accede?

- Dal terzo test si osserva che in alcuni casi (ossia per alcuni valori di d), la divisione da me implementata restituisce valori che sono più piccoli di un'unità rispetto al risultato reale. Come già ipotizzato in precedenza deve esserci qualche particolare che mi sfugge e di cui non ho tenuto conto nella fase di approssimazione; infatti se aumento i valori di q di un'unità, i test fatti mi restituiscono sempre il risultato corretto. Come mai?

Nota che se avessi avuto una potenza di 2 si poteva convertire tutto in uno shift che era ancora più veloce.

Infatti faccio:

Codice:

return v_q[d] ? (uint64_t)D * v_q[d] >> 31 + v_n[d] : D >> v_n[d];

[apatriarca]

Il prodotto finale corrisponde più o meno a moltiplicare il dividendo per una approssimazione dell'inverso del divisore facendo uso di un certo numero di cifre/bit. Se scegliamo un divisore il cui inverso ha una rappresentazione binaria infinita, come è il caso di \(9\) nel nostro esempio, allora vediamo che troncando questo inverso otterremo sempre un risultato errato per dividendi che sono multipli del divisore. Infatti la nostra approssimazione sarà sempre inferiore dell'inverso, e quindi moltiplicando per il divisore otterremo un valore più piccolo di uno che verrà troncato a zero. Lo possiamo vedere per esempio in decimale:
\[
\begin{align*}
1/9 &= 0.\overline{1} \\
[1/9]_5 &= 0.11111 \\
9 \cdot [1/9]_5 = 9 \cdot 0.11111 &= 0.99999 < 1
\end{align*}
\]
Arrotondando possiamo ottenere anche valori maggiori dell'inverso che ci permettono di avere il risultato corretto in questo caso specifico. Tuttavia non è sempre così. Se prendiamo l'inverso binario di \(9\) uguale a \(0.\overline{000111}_2\) e ci fermiamo dopo \(6\) bit, avremo semplicemente \(0.000111_2\) che moltiplicato per \(1001_2\) non ci darà il risultato sperato. Darà infatti \(0.111111_2 < 1\).

A questo punto vale la pena di considerare l'arrotondamento verso infinito. Questo ci permette di arrivare sempre all'intero successivo per multipli del divisore. A questo punto ci rimane solo da scegliere una approssimazione abbastanza vicina per cui, se \(d\) è il nostro divisore e \(\delta\) la nostra approssimazione, allora
\[ \forall k. \; \lfloor (k\,d-1)\,\delta \rfloor = k-1. \]
Sappiamo che \(k\,d\,\delta = k + k\,\epsilon\) dove l'errore \(\epsilon < 2^{1-n}\)*. \(k\) è un intero e quindi lo possiamo estrarre ed eliminare con il corrispondente valore dall'altro lato ottenendo \(\lfloor k\epsilon - \delta \rfloor = -1\). Dobbiamo quindi mostrare che \(0 > k\,\epsilon - \delta > -1 \implies k\,\epsilon < \delta\) per ogni \(k\). Ogni dividendo che prendiamo in considerazione sarà minore di \(2^{32}\) per cui scegliamo \(n\) tale che
\[ k\,\epsilon < 2^{32+1-n}/d < 1/d < \delta \implies 33 < n. \]
Abbiamo quindi ottenuto il valore e il numero di bit usato dal compilatore.

* Qui avevo inizialmente scritto \(2^n\), ma in base ai miei esperimenti sembra che l'errore sia quello che ho scritto in seguito. Fa anche tornare i conti. La differenza credo sia dovuta al fatto che ci sono due fonti di errore: l'approssimazione di \(2^n/d\) (con errore minore di \(1\) e poi lo shift \(\gg n\).

[utente__medio]

A questo punto ci rimane solo da scegliere una approssimazione abbastanza vicina per cui, se \( d \) è il nostro divisore e \( \delta \) la nostra approssimazione, allora
\[ \forall k. \; \lfloor (k\,d-1)\,\delta \rfloor = k-1. \]
Sappiamo che \( k\,d\,\delta = k + k\,\epsilon \) dove l'errore \( \epsilon < 2^{1-n} \)*. \( k \) è un intero e quindi lo possiamo estrarre ed eliminare con il corrispondente valore dall'altro lato ottenendo \( \lfloor k\epsilon - \delta \rfloor = -1 \). Dobbiamo quindi mostrare che \( 0 > k\,\epsilon - \delta > -1 \implies k\,\epsilon < \delta \) per ogni \( k \). Ogni dividendo che prendiamo in considerazione sarà minore di \( 2^{32} \) per cui scegliamo \( n \) tale che
\[ k\,\epsilon < 2^{32+1-n}/d < 1/d < \delta \implies 33 < n. \]
Abbiamo quindi ottenuto il valore e il numero di bit usato dal compilatore.

* Qui avevo inizialmente scritto \( 2^n \), ma in base ai miei esperimenti sembra che l'errore sia quello che ho scritto in seguito. Fa anche tornare i conti. La differenza credo sia dovuta al fatto che ci sono due fonti di errore: l'approssimazione di \( 2^n/d \) (con errore minore di \( 1 \) e poi lo shift \( \gg n \).

Ho provato a seguire il tuo ragionamento, ma qui mi sono perso.
Per esempio partendo dall'inizio: cosa rappresentano $k$ e $delta$ ?


P.S.1
Mi sembra di capire che "l'arrotondamento verso infinito" corrisponde più o meno alla funzione ceil(), ossia se la parte decimale è nulla restituisce la parte intera e in caso contrario restituisce la parte intera incrementata di 1. Giusto?

P.S.2
Ho avuto modo di leggere anche il precedente post che hai rimosso, ma non ho risposto subito perché volevo riflettere meglio sulle considerazioni finali che facevi.

[apatriarca]

L'idea è che sostituisci \(D/d\) con \(D \cdot q \gg 2^n\). Posso interpretare \(q\) come un numero razionale \(\delta\) rappresentato in fixed-point (credo sia virgola fissa in italiano) con \(n\) bit di parte frazionaria. A questo punto lo shift è una conversione tra virgola fissa con \(n\) bit di parte frazionaria e un normale numero intero e possiamo anche vederla come la funzione floor se interpretiamo il risultato come un numero frazionario senza parte frazionaria. Quando scrivo \(D \, \delta\) sto lavorando in virgola fissa o numeri reali mentre quando scrivo \(D \cdot q\) lo interpreto come un numero intero. Rappresento inoltre la divisione intera con \(\div\) e quella reale con \(/\).

L'arrotondamento verso infinito è ceil se il numero è positivo e floor se il numero è negativo. In pratica approssima un numero reale scegliendo l'intero più grande in valore assoluto. Di fatto siccome stiamo lavorando solo con numeri naturali qui possiamo interpretarlo come ceil. Quindi nel mio caso sto usando \(\delta = \lceil 1/d \rceil_n\) dove \(\lceil \cdot \rceil_n\) significa che sto considerando \(n\) bit di parte frazionaria.

La moltiplicazione per un numero intero costante è una funzione monotona crescente e lo shift destro mantiene questa proprietà producendo una funzione costante a tratti. La divisione intera per una costante produce una funzione costante a tratti in cui i salti avvengono in corrispondenza dei multipli del divisore (quindi numeri nella forma \(k \, d\)). Se vogliamo che le due funzioni corrispondano abbiamo bisogno che il salto avvenga in corrispondenza dei multipli e che quindi sia uguale a \(k\) per il multiplo \(k \, d\) e uguale a \(k-1\) per il valore precedente \(k \, d - 1\).

La scelta di usare ceil ci permette di stabilire che \(\delta \ge 1/d\) e che quindi \((k \, d) \, \delta \ge (k \, d)/d = k. \) Chiamo \(\epsilon = \delta - 1/d\) che sappiamo essere positivo.

A questo punto spero sia chiaro il resto, anche se mi accorgo di aver commesso un errore. Cerco di calcolare \( (k \cdot d - 1) q \gg n = \lfloor (k \, d - 1) \, \delta \rfloor \) provando sia uguale a \(k - 1\). Ho che
\[
\begin{align*}
(k \, d - 1) \, \delta &= (k \, d) \, \delta - 1 \, \delta \\
&= (k \, d)/d + (k \, d) \epsilon - \delta \\
&= k + k\,d\,\epsilon - \delta
\end{align*}
\]
A questo punto abbiamo che \(k\) è un numero intero e quindi può essere estratto dal floor. Non ci rimane che dimostrare che \(\lfloor k\,d\,\epsilon - \delta \rfloor = - 1\). Ovviamente abbiamo che \(0 < \delta < 1\) (stiamo ignorando il caso \(d = 1\)) e che \(\epsilon \ge 0\). L'importante è quindi che \(k\,d\epsilon < \delta\). A questo punto abbiamo che \(k\,d < 2^{32},\) \(\epsilon < 2^{-n}\) e \(1/q \le \delta\) possiamo farne il logaritmo ottenendo:
\[ \log_2(k\,d) + \log_2(\epsilon) < 32 - n < -\log_2(d) \le \log_2(\delta) \]
Quindi \(n > \log_2(d) + 32\).
Questo risultato ci darebbe \(n = 36\) nel nostro caso. Tuttavia c'è un problema a cui non avevo pensato. Abbiamo bisogno che \(D \cdot q\) stia in un intero a \(64\) bit. Possiamo ovviamente considerare il risultato a 128 bit del prodotto e poi ricostruire il risultato ma non credo che il compilatore lo faccia. Questo significa che è necessario ridurre i valori possibili di \(D\) a quelli che ci permettono di rimanere nell'intero a 64 bit. Quindi abbiamo che \(D = k\,d < 2^{64-n}\) e quindi abbiamo \(2n > \log_2(d) + 64\) che ci fornisce effettivamente \(34\) come il compilatore.

[utente__medio]

Innanzitutto volevo ringraziarti per la disponibilità.

Relativamente al tuo ultimo post, l'ho riletto più volte, e adesso il tuo ragionamento mi è decisamente più chiaro. Ma anche se i singoli passaggi mi sono piuttosto chiari, ancora non riesco a metabolizzare bene il tutto...

Da quello che ho capito, stai dicendo che affinché \( [D \delta] \) (con \( \delta = \lceil 1/d \rceil_n \)) sia uguale a \( [D/d] \) per ogni \( D \in [0;2^{32}) \), devono verificarsi le seguenti due uguaglianze:

\( \begin{cases} [kd \delta]=k \\ [(kd-1) \delta]=k-1 \end{cases} \)

Da cui si ricava la condizione che deve rispettare $n$, ossia \( n > \log_2(d) + 32 \). Giusto?

Mi chiedevo però se la seconda uguaglianza non dovrebbe essere invece generalizzata come \( [(kd-a) \delta]=k-1 \) con \( a \in [1;d-1] \)?

Infine se ho per esempio $d=7$ e fisso $n=11$ (e quindi \( \delta=0.00100100101 \) e $q=(100100101)_2=(293)_(10)$), come faccio a calcolarmi il massimo valore di $D$ per cui questo metodo risulta ancora funzionante?
Da un semplice programmino ottengo che è $D=684$, infatti \( 685*293 \gg 11=98\) che è diverso da \( [685/7]=97 \).

[apatriarca]

1. È corretto.

2. Stiamo facendo il floor di una funzione monotona crescente, per cui cioè il valore cresce al crescere del valore di input. Avremo quindi dei pezzi in cui il valore è costante e dei salti a determinati punti. Chiedendo che il risultato sia \(k\) ai multipli di \(d\) e ancora lo stesso valore dopo \(d-1\) è sufficiente per dimostrare che è lo stesso valore per ogni input intermedio. La dimostrazione per \(a > 1\) segue comunque facilmente dal caso \(a = 1\).

3. Non credo sia facile calcolare direttamente il risultato in questo modo. Usando l'equazione sopra ottengo infatti che è assicurato che funzioni fino a \(292\) che è ovviamente molto più piccolo del tuo valore. La ragione è che ho fatto delle maggiorazioni per arrivare a quel valore e quindi è forse possibile arrivare a valori molto più vicini. Ottieni probabilmente un valore più vicino se usi \(log_2(\epsilon)\) nella formula direttamente invece di \(-n\).

[utente__medio]

Chiaro.

Usando l'equazione sopra ottengo infatti che è assicurato che funzioni fino a $292$ che è ovviamente molto più piccolo del tuo valore.

Come hai ricavato il valore $292$?

[apatriarca]

Dalla formula (\(M\) è il massimo che vogliamo calcolare):
\[
\begin{align*}
\log_2(M) + \log_2(\epsilon) < \log_2(M) - n &< -\log_2(d) \le \log_2(\delta) \\
\log_2(M) &< n - \log_2(d) \\
M < 2^{11 - \log_2(7)} &\approx 292.57142857142867
\end{align*}
\]
Ho scritto il seguente piccolo script in Julia:

Codice:

δ(d, n) = ceil(1/d, digits=n, base=2)
ϵ(d, n) = δ(d, n) - 1/d
log₂ϵ(d, n) = log2(ϵ(d, n))
log₂M(d, n) = - log₂ϵ(d, n) - log2(d)
M(d, n) = exp2(log₂M(d, n))
M(7, 11)


che mi restituisce \(682.6666666666407\) per cui sembra che la formula \(\log_2(M) + \log_2(\epsilon) < \log_2(\delta)\) sia abbastanza accurata (la differenza di due unità potrebbe essere dovuto a qualche errore di calcolo immagino).