Ciao a tutti,
Da ieri mi incaponisco su questo esercizio, che mi chiede di trovare l'area del grafico di $f(x,y)=xy$ definito su $A={(x,y): x^2+y^2<=1 , x>=0}$
Io so che l'insieme indicato è un cerchio di raggio 1 centrato in 0, con considerati solo il primo e il quarto quadrante. Ho sostituito in coordinate polari ma probabilmente mi perdo nei passaggi algebrici perché mi dovrebbe venire un risultato con il $pi$ mentre mi ritrovo alla fine della risoluzione dell'integrale senza.
Ah, come estremi d'integrazione ho scelto $ pi/2 , (3/4) pi$ per $dtheta$ e $1,0$ per $drho$, forse sbaglio qui.
Qualcuno può dirmi come lo risolverebbe?
10 messaggi
• Pagina 1 di 1
Re: Area grafico funzione a 2 variabili
Essenzialmente è richiesto il calcolo dell'integrale di superficie: \[
||\Sigma|| := \iint\limits_{\Sigma} 1\,\text{d}S
\] con: \[
\Sigma := \left\{(x,y,z)\in\mathbb{R}^3 : z=x\,y,\,x^2+y^2\le 1,\, x\ge 0\right\}.
\] Pertanto, una parametrizzazione naturale della superficie di sostegno \(\Sigma\) è: \[
\mathbf{r}(\rho,\theta) = (\rho\cos(\theta),\,\rho\sin(\theta),\,\rho^2\cos(\theta)\sin(\theta)),
\quad
\text{con} \; (\rho,\theta) \in B := \left[0,1\right] \times \left[-\frac{\pi}{2},\frac{\pi}{2}\right]
\] da cui: \[
||\Sigma|| = \iint\limits_B ||\mathbf{r}_{\rho}(\rho,\theta) \land \mathbf{r}_{\theta}(\rho,\theta)||\,\text{d}\rho\,\text{d}\theta = \dots
\] A te concludere.
||\Sigma|| := \iint\limits_{\Sigma} 1\,\text{d}S
\] con: \[
\Sigma := \left\{(x,y,z)\in\mathbb{R}^3 : z=x\,y,\,x^2+y^2\le 1,\, x\ge 0\right\}.
\] Pertanto, una parametrizzazione naturale della superficie di sostegno \(\Sigma\) è: \[
\mathbf{r}(\rho,\theta) = (\rho\cos(\theta),\,\rho\sin(\theta),\,\rho^2\cos(\theta)\sin(\theta)),
\quad
\text{con} \; (\rho,\theta) \in B := \left[0,1\right] \times \left[-\frac{\pi}{2},\frac{\pi}{2}\right]
\] da cui: \[
||\Sigma|| = \iint\limits_B ||\mathbf{r}_{\rho}(\rho,\theta) \land \mathbf{r}_{\theta}(\rho,\theta)||\,\text{d}\rho\,\text{d}\theta = \dots
\] A te concludere.
- sellacollesella
- Average Member

- Messaggio: 328 di 959
- Iscritto il: 08/04/2022, 12:43
Re: Area grafico funzione a 2 variabili
Ciao sellacollesella,
Come mai hai inserito anche la variabile z?
Solitamente ho sempre risolto con 2, è necessario? se sì, come ti sei ricavato la sua equazione?
Come mai hai inserito anche la variabile z?
Solitamente ho sempre risolto con 2, è necessario? se sì, come ti sei ricavato la sua equazione?
- fal944
- Starting Member

- Messaggio: 20 di 23
- Iscritto il: 01/09/2022, 14:44
Re: Area grafico funzione a 2 variabili
Si tratta di una superficie non piana, ti è chiaro questo? Perché credo sia il punto cardine.
\(\quad\quad\quad\quad\quad\quad\quad\)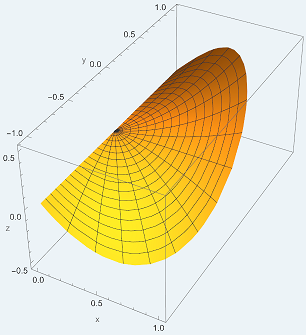
In particolare, si tratta del grafico di \(z = x\,y\) soggetto ai vincoli \(x^2+y^2 \le 1\) e \(x \ge 0\).
Per via della simmetria dei vincoli vien naturale porre \(x = \rho\cos(\theta)\) e \(y = \rho\sin(\theta)\).
Quindi, sostituendo nelle disequazioni dei vincoli, si ottiene \(0 \le \rho \le 1\) e \(-\frac{\pi}{2} \le \theta \le \frac{\pi}{2}\).
Naturalmente, ne consegue anche che \(z = (\rho\cos(\theta))(\rho\sin(\theta)) = \rho^2\cos(\theta)\sin(\theta)\).
Una volta parametrizzata la superficie è sufficiente applicare la "formulazione generale".
\(\quad\quad\quad\quad\quad\quad\quad\)

In particolare, si tratta del grafico di \(z = x\,y\) soggetto ai vincoli \(x^2+y^2 \le 1\) e \(x \ge 0\).
Per via della simmetria dei vincoli vien naturale porre \(x = \rho\cos(\theta)\) e \(y = \rho\sin(\theta)\).
Quindi, sostituendo nelle disequazioni dei vincoli, si ottiene \(0 \le \rho \le 1\) e \(-\frac{\pi}{2} \le \theta \le \frac{\pi}{2}\).
Naturalmente, ne consegue anche che \(z = (\rho\cos(\theta))(\rho\sin(\theta)) = \rho^2\cos(\theta)\sin(\theta)\).
Una volta parametrizzata la superficie è sufficiente applicare la "formulazione generale".
- sellacollesella
- Average Member

- Messaggio: 330 di 959
- Iscritto il: 08/04/2022, 12:43
Re: Area grafico funzione a 2 variabili
Se, invece, preferisci impostare il calcolo in coordinate cartesiane va comunque bene: \[
\mathbf{r}(x,y) = (x,y,f(x,y))
\quad \Rightarrow \quad
||\Sigma|| = \iint\limits_{\{x^2+y^2\le1,\,x\ge 0\}} \sqrt{1+f_x^2+f_y^2}\,\text{d}x\,\text{d}y
\] e poi passi in coordinate polari nel piano \(\langle x,y \rangle\) di centro \(O\).
\mathbf{r}(x,y) = (x,y,f(x,y))
\quad \Rightarrow \quad
||\Sigma|| = \iint\limits_{\{x^2+y^2\le1,\,x\ge 0\}} \sqrt{1+f_x^2+f_y^2}\,\text{d}x\,\text{d}y
\] e poi passi in coordinate polari nel piano \(\langle x,y \rangle\) di centro \(O\).
- sellacollesella
- Average Member

- Messaggio: 331 di 959
- Iscritto il: 08/04/2022, 12:43
Re: Area grafico funzione a 2 variabili
Grazie, chiarissimo!
Mi trovo però in difficoltà nell'impostare l'integrale, includerò $rho^3 cos(\theta)sin(\theta) drho d\theta$ ma la $z$ dove la metto?
Mi trovo però in difficoltà nell'impostare l'integrale, includerò $rho^3 cos(\theta)sin(\theta) drho d\theta$ ma la $z$ dove la metto?
- fal944
- Starting Member

- Messaggio: 21 di 23
- Iscritto il: 01/09/2022, 14:44
Re: Area grafico funzione a 2 variabili
Ciao fal944,
$z = f(x,y) = xy $
Procedendo come ha indicato sellacollesella nel suo ultimo post mi risulta:
\( \displaystyle ||\Sigma|| = \iint\limits_{\{x^2+y^2\le1,\,x\ge 0\}} \sqrt{1+f_x^2+f_y^2}\,\text{d}x\,\text{d}y = \frac{2\sqrt2 - 1}{3}\pi \)
$z = f(x,y) = xy $
Procedendo come ha indicato sellacollesella nel suo ultimo post mi risulta:
\( \displaystyle ||\Sigma|| = \iint\limits_{\{x^2+y^2\le1,\,x\ge 0\}} \sqrt{1+f_x^2+f_y^2}\,\text{d}x\,\text{d}y = \frac{2\sqrt2 - 1}{3}\pi \)
- pilloeffe
- Cannot live without

- Messaggio: 5111 di 10595
- Iscritto il: 07/02/2017, 15:45
- Località: La Maddalena - Modena
Re: Area grafico funzione a 2 variabili
Nota la parametrizzazione \((x,y,z)=\mathbf{r}(u,v)\), l'elemento d'area si scrive come \(\text{d}S = ||\mathbf{r}_u \land \mathbf{r}_v||\,\text{d}u\,\text{d}v\).
In ogni modo, credo che in questo caso ti convenga seguire l'ultima strada proposta, è meno calcolosa.
Purtroppo tendo a ricordare solo le formulazioni generali, ma non sempre è un bene, meglio pensarci su.
In ogni modo, credo che in questo caso ti convenga seguire l'ultima strada proposta, è meno calcolosa.
Purtroppo tendo a ricordare solo le formulazioni generali, ma non sempre è un bene, meglio pensarci su.
- sellacollesella
- Average Member

- Messaggio: 332 di 959
- Iscritto il: 08/04/2022, 12:43
Re: Area grafico funzione a 2 variabili
pilloeffe ha scritto:Ciao fal944,
$z = f(x,y) = xy $
Procedendo come ha indicato sellacollesella nel suo ultimo post mi risulta:
\( \displaystyle ||\Sigma|| = \iint\limits_{\{x^2+y^2\le1,\,x\ge 0\}} \sqrt{1+f_x^2+f_y^2}\,\text{d}x\,\text{d}y = \frac{2\sqrt2 - 1}{3}\pi \)
Ciao pilloeffe,
Come hai impostato l'integrale? Provo a seguire la tua strada
- fal944
- Starting Member

- Messaggio: 22 di 23
- Iscritto il: 01/09/2022, 14:44
Re: Area grafico funzione a 2 variabili
Beh, passando in coordinate polari l'integrale da risolvere è il seguente:
$\int_0^1 \int_{-\pi/2}^{\pi/2} \rho \sqrt{1 + \rho^2}\text{d}\rho \text{d}\theta = \pi \int_0^1 \rho \sqrt{1 + \rho^2}\text{d}\rho $
L'ultimo integrale è immediato perché si può facilmente ricondurre ad un integrale del tipo seguente:
$\int [g(\rho)]^a g'(\rho) \text{d}\rho = [g(\rho)]^{a + 1}/(a + 1) + c $
Passando all'integrale definito e considerando che nel caso in esame $g(\rho) = 1 + \rho^2 $ e $a = 1/2 $, si ottiene proprio il risultato che ho già scritto nel mio post precedente.
$\int_0^1 \int_{-\pi/2}^{\pi/2} \rho \sqrt{1 + \rho^2}\text{d}\rho \text{d}\theta = \pi \int_0^1 \rho \sqrt{1 + \rho^2}\text{d}\rho $
L'ultimo integrale è immediato perché si può facilmente ricondurre ad un integrale del tipo seguente:
$\int [g(\rho)]^a g'(\rho) \text{d}\rho = [g(\rho)]^{a + 1}/(a + 1) + c $
Passando all'integrale definito e considerando che nel caso in esame $g(\rho) = 1 + \rho^2 $ e $a = 1/2 $, si ottiene proprio il risultato che ho già scritto nel mio post precedente.
- pilloeffe
- Cannot live without

- Messaggio: 5112 di 10595
- Iscritto il: 07/02/2017, 15:45
- Località: La Maddalena - Modena
10 messaggi
• Pagina 1 di 1
Torna a Analisi matematica di base
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite