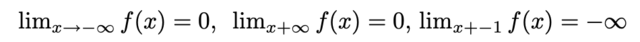Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $

[ncant]

Salve a tutti

Testo nascosto, perché contrassegnato dall'autore come fuori tema. Fai click in quest'area per vederlo.

Come state?

Come da titolo, sono qui oggi per discutere e/o ricevere consiglio riguardo questa funzione "antipatica".
Ricordo che $ \lfloor x \rfloor = \max \{ n \in \mathbb{Z} | n \leq x \} $.

Il dominio naturale risulta essere:
\[
\mathcal{D} = \mathbb{R} - \{-1 \}
\]

Ora, per quanto ne concerne i limiti, sapendo che $ (-1)^{-x} = (-1)^{x} $, si ha che
\[
- \frac{1}{1+x} \leq \frac{(-1)^{\lfloor x \rfloor}}{1+x} \leq \frac{1}{1+x}
\]

Pertanto, nel calcolo dei limiti, posso sfruttare il teorema dei carabinieri e $ \pm \frac{1}{1+x} $:
\[
\lim_{x \to \pm \infty} - \frac{1}{1+x} = \lim_{x \to \pm \infty} \frac{1}{1+x} = 0
\]
(ciò si poteva vedere pure ad occhio: alla fine l'unica cosa che può fare il numeratore è cambiare segno...)
\[
\lim_{x \to -1} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \lim_{x \to -1} \frac{(-1)^{\lfloor -1 \rfloor}}{0} = -\infty
\]

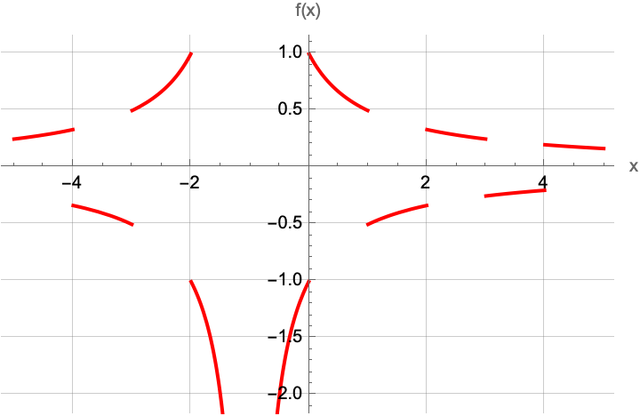
Per quanto ne concerne il segno, invece, quest'ultimo è determinato non solo dal segno del numeratore, ma da quello del denominatore. A causa di \lfloor x \rfloor, la funzione cambia segno per $ x $ intere: nell'intervallo $ (-\infty, 0) $, $ f $ è positiva negli intervalli $ (dispari, pari) $ di $ x $, mentre nell'intervallo $ (0, +\infty) $ è positiva negli intervalli $ (pari, dispari) $ di $ x $.

Dunque, di continuità e derivabilità in tutti i punti del dominio a coordinate intere non se ne parla nemmeno. Invece, $ f $ è continua in tutto il resto di $ \mathbb{D} $ in quanto somma, rapporto e composizione di funzioni elementari.

Ora, tutto quello che ho detto fin'ora sono intuizioni, che però non riesco a descrivere in matematichese. Naturalmente il Prof. non ci ha lasciato uno straccio di prova scritta o delucidazione in merito, e francamente mi aspetto anche che volesse solo due righe scritte.
Ma come dicono @pilloeffe e @gugo82, forse è meglio non fidarsi delle sole parole (i conti parlano).

Potete darmi una mano a mettere queste idee in chiaro?

P.S.: ecco un grafico di $ f $.

[Mephlip]

sapendo che $ (-1)^{-x} = (-1)^{x} $

Occhio che, quando \(x \in \mathbb{R} \setminus \mathbb{Z}\), \((-1)^x \) non è definita quando si studia analisi reale. Che significa \( (-1)^\sqrt{2} \)? Quindi, quella discussione si può fare come segue. Dato che per ogni \(x\in D\) risulta \(\lfloor x \rfloor \in \mathbb{Z} \) e quindi risulta \((-1)^{\lfloor x \rfloor} \in \{-1,1\} \), si ha: \[
0 \le \left|\frac{(-1)^{\lfloor x \rfloor}}{1+x}\right| = \frac{1}{|1+x|}
\]Il membro di destra tende a \(0\) per \(x \to \pm \infty\).

\[
\lim_{x \to -1} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \lim_{x \to -1} \frac{(-1)^{\lfloor -1 \rfloor}}{0} = -\infty
\]

A parte che c'è un errore di battitura (sostituisci e lasci la scrittura di limite), il valore del limite è giusto ma il procedimento per ottenerlo è logicamente sbagliato. Successivamente affermi correttamente che la funzione non è continua sugli interi, ma allora come ti permetti di sostituire alla funzione il valore su un intero per calcolarne il limite, che è proprio la definizione di continuità in quel punto intero? Riprova, distinguendo limite destro e sinistro e notando ad esempio che, se \(x \to -1^+\), allora puoi assumere \(-1 < x < 0 \) e quindi dedurre che \(\lfloor x \rfloor = -1\).

Il resto sul segno e sulla continuità/derivabilità lo puoi formalizzare considerando l'intervallo \([k,k+1)\) con \(k\in\mathbb{Z}\) arbitrario ed esplicitando il valore della funzione parte intera inferiore come ho fatto vedere nella discussione del limite: per ogni \(k \in \mathbb{Z}\), se \(k \le x < k+1\) allora \(\lfloor x \rfloor = k \).

Ultima nota: il grafico di \(f\), non un grafico di \(f\). Mica ce ne sono tanti .

[ncant]

Sorry per la grammatica, il copia incolla e gli orrori concettuali

Riprova, distinguendo limite destro e sinistro e notando ad esempio che, se \( x \to -1^+ \), allora puoi assumere \( -1 < x < 0 \) e quindi dedurre che \( \lfloor x \rfloor = -1 \).

Quindi, se $ x \to -1^- $, posso assumere $ -2 < x < -1 $ e quindi dedurre che \( \lfloor x \rfloor = -2 \) ? E al quel punto posso scrivere:
\[
\lim_{x \to -1^-} f(x) = \lim_{x \to 1^-} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \frac{(-1)^2}{1-1} = -\infty
\]
\[
\lim_{x \to -1^+} f(x) = \lim_{x \to 1^+} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \frac{(-1)^{-1}}{1-1} = -\infty
\]

Spero di averci azzeccato...

[Mephlip]

Esatto, a parte l'errore di battitura nell'ultimo limite da te scritto (dovrebbe essere \(x \to -1^+\)). A questo punto, se proprio vuoi scrivere \(1-1\), scrivi rispettivamente \(1-1^{-1}=0^-\) e \(1-1^+=0^+\) così si capisce come mai i limiti sono \(-\infty\) .

Se vuoi conferme sul resto, scrivi pure e lo correggiamo.

[ncant]

Esatto, a parte l'errore di battitura nell'ultimo limite da te scritto

Oh mamma. Oggi sono peggio del mio prof quando scrive i quesiti/risposte dei compiti scritti...

Se vuoi conferme sul resto, scrivi pure e lo correggiamo.

Ok, grazie

Ora, se provo ad applicare lo stesso ragionamento per una qualsiasi $ x $ intera, dovrei anche essere in grado di verificare tutte le altre, vero?

Volessi proprio scegliere una qualsiasi $ k $ arbitraria:
\[
\lim_{x \to 2^-} f(x) = \frac{(-1)^1}{1+2} = - \frac{1}{3}; \qquad \lim_{x \to 2^+} f(x) = \frac{(-1)^2}{1+2} = \frac{1}{3}
\]

Non so però se è possibile trascrivere il segno di $ f $ in un'espressione, dato che prima l'ho detta a parole... Non penso che posso scrivere "pari" e "dispari".

[Mephlip]

Prego! Ragiona in generale. Considera \(k\in\mathbb{Z}\) arbitrario fissato e calcola:\[
\lim_{x \to k^+} f(x) \\
\lim_{x \to k^-} f(x)
\]Distinguendo \(k\) pari o \(k\) dispari. Fatto ciò, per l'arbitrarietà di \(k\in\mathbb{Z}\), hai il risultato su ogni intero.

[ncant]

Notazione strana, ma

\[
\lim_{x \to k_{\text{dispari}}^-} f(x) = \frac{(-1)^{k_{\text{dispari}} - 1}}{1 + k_{\text{dispari}}} = \frac{(-1)^{k_{\text{pari}}}}{1 + k_{\text{dispari}}} = \frac{1}{1 + k_{\text{dispari}}}; \;
\lim_{x \to k_{\text{dispari}}^+} f(x) = \frac{(-1)^{k_{\text{dispari}}}}{1 + k_{\text{dispari}}} = - \frac{1}{1 + k_{\text{dispari}}}
\]

\[
\lim_{x \to k_{\text{pari}}^-} f(x) = \frac{(-1)^{k_{\text{pari}} - 1}}{1 + k_{\text{pari}}} = \frac{(-1)^{k_{\text{dispari}}}}{1 + k_{\text{pari}}} = - \frac{1}{1 + k_{\text{pari}}}; \qquad
\lim_{x \to k_{\text{pari}}^+} f(x) = \frac{(-1)^{k_{\text{pari}}}}{1 + k_{\text{pari}}} = \frac{1}{1 + k_{\text{pari}}}
\]

[Mephlip]

Sì, puoi anche alleggerire la notazione scrivendo \(k_{\text{p}}\) e \(k_{\text{d}}\). Dunque, cosa deduci da ciò?

E per la derivabilità? Sappiamo che la parte intera inferiore non è derivabile sugli interi perché, con lo stesso approccio del tuo ultimo messaggio, non è continua. Come dimostri la derivabilità della funzione parte intera inferiore in \(\mathbb{R}\setminus\mathbb{Z}\)?

[ncant]

Deduco che $ f $ non è di certo né continua né derivabile in tutti i punti del dominio a coordinate intere. Però è continua altrove (eccetto dove escluso dal dominio naturale), dato che, mentre $ \lfloor x \rfloor $ può restituire solo valori interi (per quanto da te affermato penso nel primo messaggio), il denominatore di $ f $ comunque lavora sui reali, dunque "c'è sempre una piccola variazione di$ f (x) $ quando $ x $ varia di poco" (o almeno, così dice il mio Prof, poi se è possibile formalizzarlo ancora di più, sarebbe molto meglio...).

Potrei rappresentare $ \lfloor x \rfloor $ come una serie

        Internet Explorer richiede Adobe SVG Viewer per visualizzare il grafico

\[
\lfloor x \rfloor =\sum_{n=-\infty}^{+\infty} n\ [\text{u}(t-n)-\text{u}(t-n-1) ]
\]

(in cui \( \displaystyle \text{u}(t) \) è il gradino unitario)
Ma lo trovo davvero poco intuitivo nel mio caso (poi boh...)
Mi verrebbe da dire che $ \lfloor x \rfloor $ abbia derivata prima nulla $ \forall x \in \mathbb{R} $, dato che in realtà la sua legge è quella serie.

Comunque la derivata di $ f $ è garantita (dove possibile, cioè non nelle coordinate intere e in $ x = -1 $) da teoremi analoghi a quelli delle funzioni continue che coinvolgono la somma, prodotto, composizione... di funzioni continue (tanto \lfloor x \rfloor restituisce solo valori interi...)

[Mephlip]

Niente serie direi. Il punto è che non so/non ricordo se hai già dimostrato che \(\lfloor x \rfloor \) è continua in \(\mathbb{R}\setminus\mathbb{Z}\). Perché, se non lo hai fatto, non puoi usare i teoremi di regolarità per dedurre la continuità di \(f\), in quanto appunto non sai se il numeratore è continuo o no. Prova a dimostrarlo ora.

Stesso problema per la derivabilità: il ragionamento va bene, ma hai dimostrato che \(\lfloor x \rfloor\) è derivabile in \(\mathbb{R}\setminus\mathbb{Z}\)? Se no, prova a farlo ora.