Sento che dovrei usare la solita formula per la derivabilità ma usando un generico $ x_0 \ne \mathbb{Z} $, ma mi sfugge...
Posso comprare una vocale?
31 messaggi
• Vai alla pagina... • 1, 2, 3, 4
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
Il mio rapporto con la matematica è come quello tra Dante e Beatrice: la amo, ma è un'amore non corrisposto.
-

ncant - Junior Member

- Messaggio: 79 di 102
- Iscritto il: 16/12/2023, 15:57
- Località: qualche volta a Roma, qualche volta a Pisa
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
Sì: hai che \(h \to 0\). rileggi la discussione e rifletti su questo.
A spoon can be used for more than just drinking soup. You can use it to dig through the prison you're locked in, or as a weapon to gouge the witch's eyes out. Of course, you can also use the spoon to continually sip the watery soup inside your eternal prison.
-

Mephlip - Moderatore globale

- Messaggio: 2305 di 3664
- Iscritto il: 03/06/2018, 23:53
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
Sarà mica che:
per $ x \in \mathbb{R} \setminus \mathbb{Z} $
\[
\lim_{h \to 0} \frac{\lfloor x_0 + h \rfloor - \lfloor x_0 \rfloor}{h} = \lim_{h \to 0} \frac{t - t}{h} = 0
\]
dove $ t \in \mathbb{Z} $ ed è il valore restituito da $ \lfloor x \rfloor $?
per $ x \in \mathbb{R} \setminus \mathbb{Z} $
\[
\lim_{h \to 0} \frac{\lfloor x_0 + h \rfloor - \lfloor x_0 \rfloor}{h} = \lim_{h \to 0} \frac{t - t}{h} = 0
\]
dove $ t \in \mathbb{Z} $ ed è il valore restituito da $ \lfloor x \rfloor $?
Il mio rapporto con la matematica è come quello tra Dante e Beatrice: la amo, ma è un'amore non corrisposto.
-

ncant - Junior Member

- Messaggio: 80 di 102
- Iscritto il: 16/12/2023, 15:57
- Località: qualche volta a Roma, qualche volta a Pisa
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
A parte la confusione con la notazione (appaiono sia \(x\) sia \(x_0\)), è giusto. Però, per essere proprio pedante, mi dimostri che \(\lfloor x_0+h \rfloor = \lfloor x_0 \rfloor\) quando \(h \to 0\) e \(x_0 \in \mathbb{R}\setminus\mathbb{Z}\)?
A spoon can be used for more than just drinking soup. You can use it to dig through the prison you're locked in, or as a weapon to gouge the witch's eyes out. Of course, you can also use the spoon to continually sip the watery soup inside your eternal prison.
-

Mephlip - Moderatore globale

- Messaggio: 2306 di 3664
- Iscritto il: 03/06/2018, 23:53
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
Intuitivamente, $ h $ è un incremento davvero piccolo, dunque, per $ x_0 \ne \mathbb{Z} $ , $ \lfloor x_0 + h \rfloor = x_0 $, ma devo allora trovare un altro modo...  ...
...
Sia $ x \in \mathbb{R} $ e sia $ n \in \mathbb{Z} $. Sia $ m = \lfloor x \rfloor \in \mathbb{Z} $.
Allora $ x = m + e $ con $ e \in \mathbb{R} $ e $ 0 \leq e < 1 $.
Allora
\[ \lfloor x + n \rfloor = \lfloor ( m + e ) + n \rfloor = \lfloor ( m + n ) + e \rfloor = m + n = \lfloor x \rfloor + n \]
Ma così lo dimostro per $ x $ appartenenti a tutto $ \mathbb{R} $...
Potrebbe anche questo essere un granchio enorme...
 ...
...Sia $ x \in \mathbb{R} $ e sia $ n \in \mathbb{Z} $. Sia $ m = \lfloor x \rfloor \in \mathbb{Z} $.
Allora $ x = m + e $ con $ e \in \mathbb{R} $ e $ 0 \leq e < 1 $.
Allora
\[ \lfloor x + n \rfloor = \lfloor ( m + e ) + n \rfloor = \lfloor ( m + n ) + e \rfloor = m + n = \lfloor x \rfloor + n \]
Ma così lo dimostro per $ x $ appartenenti a tutto $ \mathbb{R} $...

Potrebbe anche questo essere un granchio enorme...
Il mio rapporto con la matematica è come quello tra Dante e Beatrice: la amo, ma è un'amore non corrisposto.
-

ncant - Junior Member

- Messaggio: 81 di 102
- Iscritto il: 16/12/2023, 15:57
- Località: qualche volta a Roma, qualche volta a Pisa
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
Attendendo la conferma dell'ultimo messaggio, pongo l'attenzione sulla risposta fornita dal nostro docente in merito ai minimi e massimi di $ f $:
Il grafico tuttavia, in merito ai massimi, dice diversamente:
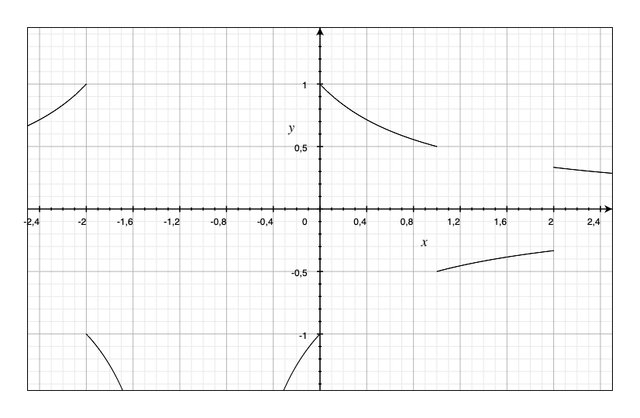
Troppo pignolo?
"[2] Quali sono massimo, minimo sup e inf dei valori assunti dalla funzione?
Ci sono infiniti massimi locali?
R: Il minino non esiste. Il sup e il massimo sono uguali a 2: Ci sono massimi locali ad es. in tutti i punti di coordinata pari e positiva. Quindi sono infiniti."
Ci sono infiniti massimi locali?
R: Il minino non esiste. Il sup e il massimo sono uguali a 2: Ci sono massimi locali ad es. in tutti i punti di coordinata pari e positiva. Quindi sono infiniti."
Il grafico tuttavia, in merito ai massimi, dice diversamente:

Troppo pignolo?
Ultima modifica di ncant il 07/02/2024, 14:51, modificato 2 volte in totale.
Il mio rapporto con la matematica è come quello tra Dante e Beatrice: la amo, ma è un'amore non corrisposto.
-

ncant - Junior Member

- Messaggio: 83 di 102
- Iscritto il: 16/12/2023, 15:57
- Località: qualche volta a Roma, qualche volta a Pisa
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
ncant ha scritto:Intuitivamente, $ h $ è un incremento davvero piccolo, dunque, per $ x_0 \ne \mathbb{Z} $ , $ \lfloor x_0 + h \rfloor = x_0 $
No, proprio perché \(h\) puoi prenderlo piccolo abbastanza è \(\lfloor x_0 + h \rfloor = \lfloor x_0 \rfloor\).
ncant ha scritto:Sia $ x \in \mathbb{R} $ e sia $ n \in \mathbb{Z} $. Sia $ m = \lfloor x \rfloor \in \mathbb{Z} $.
Allora $ x = m + e $ con $ e \in \mathbb{R} $ e $ 0 \leq e < 1 $.
Allora
\[ \lfloor x + n \rfloor = \lfloor ( m + e ) + n \rfloor = \lfloor ( m + n ) + e \rfloor = m + n = \lfloor x \rfloor + n \]
Ma così lo dimostro per $ x $ appartenenti a tutto $ \mathbb{R} $...
Così hai dimostrato un'altra cosa: la parte intera di una somma si può scrivere come somma di due interi. Non è quello che volevamo. Si può dimostrare come segue (ricalcando quanto già detto prima sulla continuità): sia \(x_0 \in \mathbb{R}\setminus\mathbb{Z}\) arbitrario. Per cose già dette prima in questo post, esiste \(k_0 \in \mathbb{Z}\) tale che \(k_0 < x < k_0+1\). Quindi, se \(0<|h|<\text{min}\{|x_0-k_0|,|x_0-(k_0 +1)|\}\) allora \(x_0+h \in (k_0,k_0+1)\) e perciò \(\lfloor x_0+h \rfloor = k_0 = \lfloor x_0 \rfloor\). Dunque, il rapporto incrementale relativo alla funzione parte intera inferiore calcolato in \(x_0\) è identicamente nullo e pertanto è minore di qualsiasi \(\varepsilon>0\) arbitrario. Questo dimostra che sia il limite destro del rapporto incrementale in \(x_0\) sia il limite sinistro del rapporto incrementale in \(x_0\) sono nulli. Quindi, la funzione parte intera inferiore è derivabile in \(\mathbb{R}\setminus\mathbb{Z}\) con derivata nulla (come ci aspettavamo dal grafico, essendo essa costante "a tratti" negli intervalli chiusi a sinistra e aperti a destra aventi interi consecutivi come estremi).
Per quanto riguarda l'altra domanda: innanzitutto, per favore, sostituisci il testo della foto con le formule scritte. Il grafico puoi lasciarlo; grazie! Non sei troppo pignolo: è giusto quello che dici. Molto probabilmente è un errore di battitura, voleva scrivere che il massimo è \(1\).
A spoon can be used for more than just drinking soup. You can use it to dig through the prison you're locked in, or as a weapon to gouge the witch's eyes out. Of course, you can also use the spoon to continually sip the watery soup inside your eternal prison.
-

Mephlip - Moderatore globale

- Messaggio: 2309 di 3664
- Iscritto il: 03/06/2018, 23:53
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
Mephlip ha scritto:Per quanto riguarda l'altra domanda: innanzitutto, per favore, sostituisci il testo della foto con le formule scritte. Il grafico puoi lasciarlo. Non sei troppo pignolo: è giusto quello che dici. Molto probabilmente è un errore di battitura, voleva scrivere che il massimo è \(1\).
Done
Oddio... non so davvero come ringraziarti per quella risposta eccezionale
Quindi... dimostrato dove $ \lfloor x \rfloor $ è continuo in $ \mathbb{R} $, posso affermare che $ f $ è continua e derivabile $ forall x \in \mathbb{R} \ \setminus \ \mathbb{Z} $ in quanto si tratta del rapporto di due funzioni continue nel dominio in questione?
Poi, per la monotonia e la convessità posso sfruttare $ \frac{1}{| x + 1 |} $ e $ - \frac{1}{|x + 1|} $ quando $ f $ è rispettivamente positiva o negativa (per il teorema dei carabinieri)?
Il mio rapporto con la matematica è come quello tra Dante e Beatrice: la amo, ma è un'amore non corrisposto.
-

ncant - Junior Member

- Messaggio: 84 di 102
- Iscritto il: 16/12/2023, 15:57
- Località: qualche volta a Roma, qualche volta a Pisa
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
Prego! E grazie per aver modificato  .
.
Ribadisco: la funzione \(\lfloor x \rfloor\) non è continua in \(\mathbb{R}\), è continua in \(\mathbb{R}\setminus \mathbb{Z}\). È tipo la decima volta che lo diciamo, spero che il tuo sia un errore di battitura .
.
Sì. Devi giusto aggiungere che \((-1)^{\lfloor x \rfloor}\) è continua in \(\mathbb{R}\setminus\mathbb{Z}\) perché composizione tra una potenza e una parte intera inferiore. Le potenze sono continue in \(\mathbb{R}\), quindi lo sono in particolare in \(x=-1\).
Consideri \(k \in \mathbb{Z}\setminus\{-1\}\), separi i casi \(k\) pari o \(k\) dispari e consideri \(x \in [k,k+1)\). Da qui, in base alla parità/disparità di \(k\), hai le due funzioni \(x \mapsto 1/(x+1)\) o \(x \mapsto -1/(x+1)\) la cui monotonia/convessità è semplice da stabilire.
Non ho capito cosa c'entra il teorema dei carabinieri però: il segno lo hai già discusso, il teorema dei due carabinieri è un teorema per calcolare i limiti.
 .
.ncant ha scritto:Quindi... dimostrato dove $ \lfloor x \rfloor $ è continuo in $ \mathbb{R} $
Ribadisco: la funzione \(\lfloor x \rfloor\) non è continua in \(\mathbb{R}\), è continua in \(\mathbb{R}\setminus \mathbb{Z}\). È tipo la decima volta che lo diciamo, spero che il tuo sia un errore di battitura
 .
.ncant ha scritto:posso affermare che $ f $ è continua e derivabile $ forall x \in \mathbb{R} \ \setminus \ \mathbb{Z} $ in quanto si tratta del rapporto di due funzioni continue nel dominio in questione?
Sì. Devi giusto aggiungere che \((-1)^{\lfloor x \rfloor}\) è continua in \(\mathbb{R}\setminus\mathbb{Z}\) perché composizione tra una potenza e una parte intera inferiore. Le potenze sono continue in \(\mathbb{R}\), quindi lo sono in particolare in \(x=-1\).
ncant ha scritto:per la monotonia e la convessità posso sfruttare $ \frac{1}{| x + 1 |} $ e $ - \frac{1}{|x + 1|} $ quando $ f $ è rispettivamente positiva o negativa
Consideri \(k \in \mathbb{Z}\setminus\{-1\}\), separi i casi \(k\) pari o \(k\) dispari e consideri \(x \in [k,k+1)\). Da qui, in base alla parità/disparità di \(k\), hai le due funzioni \(x \mapsto 1/(x+1)\) o \(x \mapsto -1/(x+1)\) la cui monotonia/convessità è semplice da stabilire.
ncant ha scritto:(per il teorema dei carabinieri)?
Non ho capito cosa c'entra il teorema dei carabinieri però: il segno lo hai già discusso, il teorema dei due carabinieri è un teorema per calcolare i limiti.
A spoon can be used for more than just drinking soup. You can use it to dig through the prison you're locked in, or as a weapon to gouge the witch's eyes out. Of course, you can also use the spoon to continually sip the watery soup inside your eternal prison.
-

Mephlip - Moderatore globale

- Messaggio: 2310 di 3664
- Iscritto il: 03/06/2018, 23:53
Re: Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
Mephlip ha scritto:Ribadisco: la funzione \(\lfloor x \rfloor\) non è continua in \(\mathbb{R}\), è continua in \(\mathbb{R}\setminus \mathbb{Z}\). È tipo la decima volta che lo diciamo, spero che il tuo sia un errore di battitura.
Intendevo: in quali parti di $ \mathbb{R} $ $ \lfloor x \rfloor $ è continua. Poi abbiamo già dimostrato che in effetti è continua solo in $ \mathbb{R} \setminus \mathbb{Z} $. Solo che nella mia interpretazione, essendo $ \mathbb{R} \setminus \mathbb{Z} $ un sottoinsieme di $ \mathbb{R} $, lo ho interpretato come la domanda "dove è $ \lfloor x \rfloor $ continuo in $ \mathbb{R} $? La risposta è che è continua per $ \mathbb{R} \setminus \mathbb{Z} $.
(Ragionamento storto, nevvero?)
Mephlip ha scritto:Sì. Devi giusto aggiungere che \((-1)^{\lfloor x \rfloor}\) è continua in \(\mathbb{R}\setminus\mathbb{Z}\) perché composizione tra una potenza e una parte intera inferiore. Le potenze sono continue in \(\mathbb{R}\), quindi lo sono in particolare in \(x=-1\).
Okie
Mephlip ha scritto:Consideri \(k \in \mathbb{Z}\setminus\{-1\}\), separi i casi \(k\) pari o \(k\) dispari e consideri \(x \in [k,k+1)\). Da qui, in base alla parità/disparità di \(k\), hai le due funzioni \(x \mapsto 1/(x+1)\) o \(x \mapsto -1/(x+1)\) la cui monotonia/convessità è semplice da stabilire.
Come funzione a tratti diventa (considerando $ k \in \mathbb{Z}\setminus\{-1\} $ e $ x \in [k,k+1) $ )
\[
f(x) := \begin{cases}
- \frac{1}{x + 1} & \text{per } k \text{ dispari } \\
\frac{1}{x + 1} & \text{per } k \text{ pari }
\end{cases}
\]
(sono ancora alla ricerca di una notazione migliore...)
Mephlip ha scritto:ncant ha scritto:(per il teorema dei carabinieri)?
Non ho capito cosa c'entra il teorema dei carabinieri però: il segno lo hai già discusso, il teorema dei due carabinieri è un teorema per calcolare i limiti.
Sono rincoglionito e raffreddato. E sparo ca**ate (quest'ultima rimane invariata anche se sono in salute).
Ultima modifica di ncant il 07/02/2024, 18:25, modificato 1 volta in totale.
Il mio rapporto con la matematica è come quello tra Dante e Beatrice: la amo, ma è un'amore non corrisposto.
-

ncant - Junior Member

- Messaggio: 85 di 102
- Iscritto il: 16/12/2023, 15:57
- Località: qualche volta a Roma, qualche volta a Pisa
31 messaggi
• Vai alla pagina... • 1, 2, 3, 4
Torna a Analisi matematica di base
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite