Problema con sfera e piano tangente

[ZfreS]

Ah, ora ho capito: il vettore normale al piano è $n=(h, k, -h)$ che deve essere proporzionale a $PC$, ovvero
$(h, k, -h) = lambda(x_p-1, y_p+2, z_p+1)$ con $lambda != 0$.

[sellacollesella]

E anche questa l'abbiamo portata a casa.

Il passo successivo consiste nella risoluzione di quel sistema di equazioni rispetto a \(x_p\), \(y_p\) e \(z_p\).

Quindi, dovrai imporre che \(P\) appartenga sia alla sfera che al fascio di piani determinando \(h\) e \(k\).

Infine dovresti essere in grado di concludere in autonomia. Provaci.

[ZfreS]

Ok, facendo come dici, trovo prima $x_p, y_p, z_p $ in funzione di di $h, k, lambda$ :
$\{(x_p = (h+lambda)/lambda), (y_p=(k-2lambda)/lambda), (z_p= (-h-lambda)/lambda):}$
Poi impongo il passaggio per la sfera e ottengo l'equazione:
$2h^2+2k^2-10lambda^2 = 0$
Poi impongo il passaggio per il piano e ottengo, posto $lambda != 0$:
$2h^2-hlambda+k^2-3klambda=0$.
Mi manca ancora una condizione per determinare $h, k, lambda$. Cosa sto dimenticando?

[sellacollesella]

trovo prima $x_p, y_p, z_p $ in funzione di di $h, k, lambda$ :
$\{(x_p = (h+lambda)/lambda), (y_p=(k-2lambda)/lambda), (z_p= (-h-lambda)/lambda):}$

Ok.

Poi impongo il passaggio per la sfera e ottengo l'equazione:
$2h^2+2k^2-10lambda^2 = 0$

Rivedi i conti, deve uscire \(2h^2+k^2-9\lambda^2=0\).

Poi impongo il passaggio per il piano e ottengo, posto $lambda != 0$:
$2h^2-hlambda+k^2-3klambda=0$.

Ok.

Mi manca ancora una condizione per determinare $h, k, lambda$.

Non manca nulla, in quanto a noi basta determinare \(h\) e \(k\) in funzione di \(\lambda\).

[ZfreS]

Ok, ho capito, se non sbaglio i conti, dovrebbe venire $h = (9sqrt(19)lambda^2)/19$ e
$k = lambdasqrt((171-lambda^2)/19)$

[sellacollesella]

Posto \(\lambda \ne 0\), per risolvere il seguente sistema di equazioni: \[
\begin{cases}
2h^2+k^2-9\lambda^2=0\\
2h^2+k^2-\lambda h-3\lambda k=0\\
\end{cases}
\] è sufficiente sottrarre alla prima equazione la seconda equazione, da cui: \[
-9\lambda^2+\lambda h+3\lambda k = 0
\quad \quad \Leftrightarrow \quad \quad h = 9\lambda - 3k.
\] Quindi, sostituendo tale espressione nella prima equazione, si ottiene: \[
2(9\lambda - 3k)^2+k^2-9\lambda^2=0
\quad \quad \Leftrightarrow \quad \quad
k = 3\lambda \, \vee \, k = \frac{51}{19}\lambda
\] da cui le due soluzioni del sistema in esame: \[
(h,k) = (0,3\lambda) \; \vee \; (h,k) = \left(\frac{18}{19}\lambda,\frac{51}{19}\lambda\right).
\] Quindi, che ce ne facciamo di queste due coppie?

[ZfreS]

Grazie, evidentemente ho fatto errori di calcolo con una procedura che mi ha complicato la vita, ora trovati h e k si sostituiscono nell'equazione del fascio di piani, in cui rimane il parametro $lambda$: $18/19lambda(x-z-3)+51/19lambda(y-1)=0$ e sempre supponendo $lambda!=0$ si ottiene $18x+51y-18z-105=0$.

[sellacollesella]

Sì, quello è un piano (se dividi per 3 si semplifica). Poi va considerata anche l'altra soluzione, da cui: \[
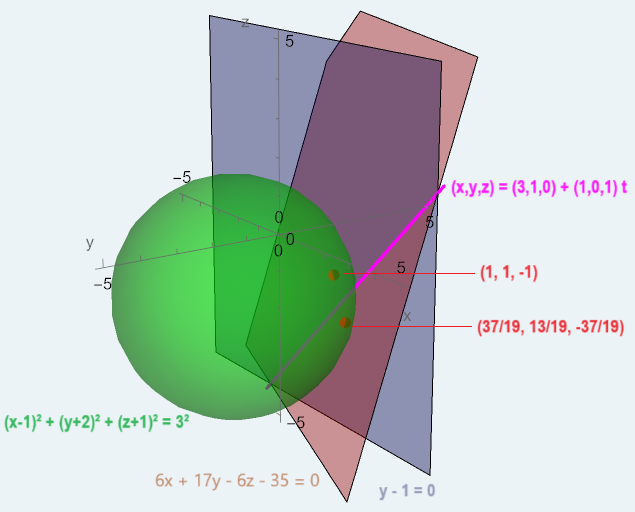
\boxed{6x + 17y - 6z - 35 = 0 \quad \quad \quad y - 1 = 0}
\] In definitiva, gli oggetti geometrici manipolati in questo problema sono di seguito graficati:

[ZfreS]

Bello, cosa hai usato per il disegno?

[sellacollesella]

Mathematica.