Chiedo la correzione per sapere se ho interpretato e analizzato bene la struttura.
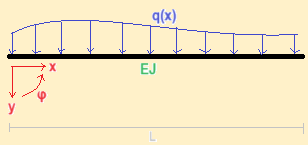
Testo:

Svolgimento:







sellacollesella ha scritto:Se non l'avete vista, poco male, ci facciamo bastare il principio dei lavori virtuali, ci metteremo qualche minuto in più rispetto all'integrazione della linea elastica ma arriveremo allo stesso e identico risultato.
Nella fattispecie, ora dell'iperstatica possiamo tranquillamente dimenticarci, dato che i conti di cui sopra permettono di considerare un'isostatica associata del tutto equivalente, ossia una mensola incastrata all'estremo sinistro, con un carico distribuito verticalmente, in giù, di intensità \(q\) e una forza applicata all'estremo destro libero: verticale, in su e di intensità \(81qL/74\).
Pertanto, non sapendo a priori in che punto calcolare l'abbassamento della mensola, applichiamo una forza fittizia verticale, rivolta verso il basso ad una generica distanza \(x\) dall'estremo sinistro e di conseguenza ad una generica distanza \(3L-x\) dall'estremo destro, essendo \(3L\) la lunghezza della mensola in esame.
Ciò fatto, basterà calcolare il momento flettente nel tratto a sinistra e nel tratto a destra di tale forza, quindi integrare applicando il principio dei lavori virtuali, ad esempio seguendo la strategia che hai applicato sopra.
Quello che otterremo è un abbassamento \(v(x)\) con \(0 \le x \le 3L\), che trattandosi di una funzione continua in un insieme chiuso e limitato il teorema di Weierstrass ci garantisce ammettere minimo e massimo assoluti, determinabili come appreso nel corso di analisi matematica uno. Il massimo è ciò che è richiesto dal testo.


giuliob94 ha scritto:Mi sono guardato la teoria della linea elastica e ho svolto così [...]
φ[x_] = -y'[x];
M[x_] = -e j y''[x];
T[x_] = -e j y'''[x];
j = a l^2/2;
k = 2 e a/l;
DSolve[{
y''''[x] == q/(e j),
y[0] == 0,
φ[0] == 0,
M[3 l] == 0,
T[3 l] == -k y[3 l]
}, y[x], x] // Expand
{{y[x] -> (45 q x^2)/(37 a e) - (47 q x^3)/(74 a e l) + (q x^4)/(12 a e l^2)}}FullSimplify[Maximize[{y[x], 0 <= x <= 3 l}, x], {e > 0, a > 0, l > 0, q > 0}]{(81 (1788231 + 33229 Sqrt[2121]) l^2 q)/(239892608 a e), {x -> (360 l)/(141 + Sqrt[2121])}}{(1.12052 l^2 q)/(a e), {x -> 1.92457 l}}giuliob94 ha scritto:per quanto riguarda questo metodo agisco così? [...]


Visitano il forum: Nessuno e 1 ospite