Data la seguente
struttura isostatica:
\(\quad\quad\quad\quad\quad\quad\)
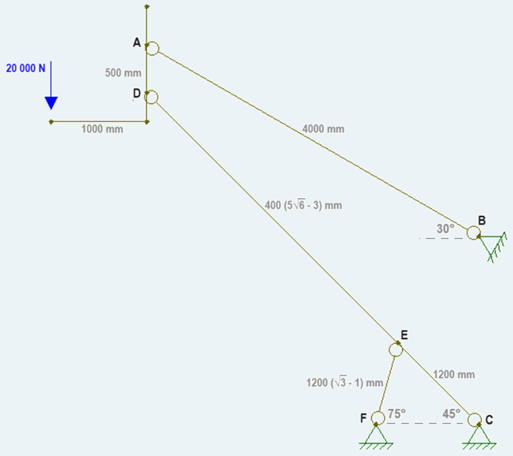
essendo categoricamente fuori discussione che si possano determinare le
reazioni vincolari esterne senza esplodere la struttura (lo hai già sperimentato sulla tua pelle), possiamo esploderla in almeno due modi:
- in modo ingenuo esplodendo tutti i corpi indistintamente, quindi risolvendo un sistema di dodici equazioni lineari in dodici incognite (è ciò che potrebbe fare un software, ma a mano anche no);
- in modo intelligente esplodendo tutti i corpi tenendo però conto che \(AB\) ed \(EF\) sono due bielle (o
due pendoli, che dir si voglia), quindi risolvendo un sistema di sei equazioni lineari in sei incognite.
Pertanto, esplodendo la struttura in modo
intelligente, si ha:
\(\quad\quad\)

e imponendo l'
equilibrio di ogni corpo esploso, si ottiene: \[
\begin{cases}
H_D + N_{AB}\cos(30°) = 0 \\
V_D - N_{AB}\sin(30°) - 20000 = 0 \\
(20000)(1000) - (N_{AB}\cos(30°))(500) = 0 \\
\\
H_C - H_D - N_{EF}\cos(75°) = 0 \\
V_C - V_D - N_{EF}\sin(75°) = 0 \\
(H_C+V_C)\frac{1200}{\sqrt{2}} + (H_D+V_D)\frac{400(5\sqrt{6}-3)}{\sqrt{2}} = 0 \\
\end{cases}
\quad \quad \Leftrightarrow \quad \quad
\begin{cases}
N_{AB} = +46188\,N \\
N_{EF} = -10313\,N \\
\\
H_C = -42669\,N \\
V_C = +33132\,N \\
\\
H_D = -40000\,N \\
V_D = +43094\,N \\
\end{cases}.
\]
A questo punto e solo a questo punto è possibile assecondare i capricci del vostro docente.

Vuole le
reazioni vincolari esterne? Eccole: \[
\begin{aligned}
& \mathbf{R}_B = \left(+40000,\,-23094\right)N; \\
& \mathbf{R}_C = \left(-42669,\,+33132\right)N; \\
& \mathbf{R}_F = \left(+2669,\,+9962\right)N. \\
\end{aligned}
\] Vuole le
caratteristiche della sollecitazione? Eccole: \[
\begin{aligned}
& \begin{cases}
N_{AB}(s) = +46188\,N \\
T_{AB}(s) = 0 \\
M_{AB}(s) = 0 \\
\end{cases} \quad \quad 0 \le s \le 4000\,mm; \\
\\
& \begin{cases}
N_{CE}(s) = -53600\,N \\
T_{CE}(s) = +6744\,N \\
M_{CE}(s) = -6744\,s\,Nmm \\
\end{cases} \quad \quad 0 \le s \le 1200\,mm; \\
\\
& \begin{cases}
N_{DE}(s) = -58756\,N \\
T_{DE}(s) = -2188\,N \\
M_{DE}(s) = -2188\,s\,Nmm \\
\end{cases} \quad \quad 0 \le s \le 400\left(5\sqrt{6}-3\right)mm; \\
\\
& \begin{cases}
N_{EF}(s) = -10313\,N \\
T_{EF}(s) = 0 \\
M_{EF}(s) = 0 \\
\end{cases} \quad \quad 0 \le s \le 1200\left(\sqrt{3}-1\right)mm. \\
\end{aligned}
\] Vuole la
verifica a resistenza nelle sezioni più sollecitate? E verifica sia!
Tenendo conto che si tratta di sezioni circolari piene, area e momento d'inerzia risultano essere: \[
A = \frac{\pi}{4}(60\,mm)^2 = 2827\,mm^2,
\quad \quad \quad
J = \frac{\pi}{64}(60\,mm)^4 = 636173\,mm^4
\] e considerando la sezione \(E\) intesa come sezione finale di \(CE\), dove: \[
N_E = -53600\,N,
\quad \quad \quad
T_E = +6744\,N,
\quad \quad \quad
M_E = -8092613\,Nmm
\] le tensioni minime e massime si trovano al bordo e in mezzeria: \[
\small
\begin{aligned}
& \sigma_z = \frac{N_E}{A} + \frac{M_E}{J}(-30\,mm) = 363\,\text{MPa},
\quad \tau_z = 0, \quad \sigma_{\text{id,VM}}=\sqrt{\sigma_z^2+3\tau_z^2} = 363\,\text{MPa}; \\
& \sigma_z = \frac{N_E}{A} + \frac{M_E}{J}(0\,mm) = -18.96\,\text{MPa},
\quad \tau_z = \frac{4}{3}\frac{T_E}{A} = 3.18\,\text{MPa}, \quad \sigma_{\text{id,VM}}=\sqrt{\sigma_z^2+3\tau_z^2} = 19.74\,\text{MPa}; \\
& \sigma_z = \frac{N_E}{A} + \frac{M_E}{J}(+30\,mm) = -401\,\text{MPa},
\quad \tau_z = 0, \quad \sigma_{\text{id,VM}}=\sqrt{\sigma_z^2+3\tau_z^2} = 401\,\text{MPa}; \\
\end{aligned}
\] dove al bordo la verifica non è soddisfatta perché le tensioni \(\sigma_{\text{id}}\) eccedono quella ammissibile.
Analogamente, considerando la sezione \(E\) intesa come sezione finale di \(DE\), dove: \[
N_E = -58756\,N,
\quad \quad \quad
T_E = -2188\,N,
\quad \quad \quad
M_E = -8092613\,Nmm
\] le tensioni minime e massime si trovano al bordo e in mezzeria: \[
\small
\begin{aligned}
& \sigma_z = \frac{N_E}{A} + \frac{M_E}{J}(-30\,mm) = 361\,\text{MPa},
\quad \tau_z = 0, \quad \sigma_{\text{id,VM}}=\sqrt{\sigma_z^2+3\tau_z^2} = 361\,\text{MPa}; \\
& \sigma_z = \frac{N_E}{A} + \frac{M_E}{J}(0\,mm) = -20.78\,\text{MPa},
\quad \tau_z = \frac{4}{3}\frac{T_E}{A} = -1.03\,\text{MPa}, \quad \sigma_{\text{id,VM}}=\sqrt{\sigma_z^2+3\tau_z^2} = 20.86\,\text{MPa}; \\
& \sigma_z = \frac{N_E}{A} + \frac{M_E}{J}(+30\,mm) = -402\,\text{MPa},
\quad \tau_z = 0, \quad \sigma_{\text{id,VM}}=\sqrt{\sigma_z^2+3\tau_z^2} = 402\,\text{MPa}; \\
\end{aligned}
\] dove al bordo la verifica non è soddisfatta perché le tensioni \(\sigma_{\text{id}}\) eccedono quella ammissibile.
Dulcis in fundo, non rimane che considerare la biella \(AB\) (tirante) e la biella \(EF\) (puntone): \[
\sigma_{\text{id,AB}} = \frac{\left|N_{AB}\right|}{A} = 16.34\,\text{MPa},
\quad \quad \quad
\sigma_{\text{id,EF}} = \frac{\left|N_{EF}\right|}{A} = 3.65\,\text{MPa}
\] per le quali la
verifica a resistenza è banalmente soddisfatta. D'altro canto, a rigore, per i puntoni
risulta necessario verificare anche l'
instabilità elastica per carico di punta. In particolare, essendo: \[
\rho_{\min} = \sqrt{\frac{J_{\min}}{A}} = 15\,mm, \quad \quad \lambda = \frac{L_{\text{eq}}}{\rho_{\min}} = 58.56
\] allora le
tensioni critiche secondo Eulero e secondo Johnson risultano essere: \[
\sigma_E = \frac{\pi^2E}{\lambda^2} = 604\,\text{MPa}, \quad \quad \sigma_J = \sigma_{\text{yd}} - \frac{\sigma_{\text{yd}}^2}{4\,\sigma_E} = 255\,\text{MPa}
\] dove per qualsiasi acciaio \(E = 210\,000\,\text{MPa}\), mentre per quello qui considerato \(\sigma_{\text{yd}}=290\,\text{MPa}\).
Pertanto, essendo \(\sigma_E > \sigma_{\text{yd}}/2\) ne consegue che \(\sigma_{\text{lim}} = \sigma_J\), da cui la verifica: \[
\sigma_{\text{id,EF}} \le \sigma_{\text{lim}}
\] risulta soddisfatta (d'altronde, c'era da aspettarselo, vista l'esigua tensione nel puntone).







