Leggendo alcune discussioni in vari forum con un bacino d'utenza più o meno grande, ho notato che la maggior parte delle persone è nella mia stessa situazione, ossia non ha la più pallida idea di come vengano effettivamente computate le funzioni elementari, perlomeno quelle di base quali seno, coseno, arcotangente, esponenziale naturale e logaritmo naturale.
Pertanto, ho pensato di condividere con voi alcune nozioni che ho messo da parte in questi ultimi giorni di studio autonomo, con la ovvia premessa di prendere tutto con il beneficio del dubbio, essendo esperto del nulla avrò compreso tali nozioni sicuramente in modo ingenuo, senza solide conoscenze di matematica e di informatica che indubbiamente sono necessarie per mettere in piedi un discorso serio.
NEL PASSATO
Un primo modo per computare tali funzioni elementari consiste di sole addizioni, sottrazioni, spostamento di bit e tabelle di ricerca, indispensabile quando non è disponibile alcun moltiplicatore hardware (ad esempio, in semplici microcontrollori e FPGA). Ecco, questo è ciò che fa CORDIC, algoritmo ideato da Volder nel 1956 per le funzioni seno e coseno, quindi esteso da Walther nel 1971 alle funzioni iperboliche, esponenziali e logaritmi naturali, ... che ha permesso sostanzialmente il lancio della prima calcolatrice tascabile, ossia la mitica HP-35.
D'altro canto, oggigiorno la tecnologia a diposizione è decisamente più avanzata rispetto a 50 anni fa, quindi non è affatto detto che sia necessario passare per il suddetto algoritmo, bensì si può optare a qualcosa di più efficiente. Nella fattispecie, l'idea alla base è cominciare scopiazzando da CORDIC, ossia attraverso una riduzione di portata dell'input ricondursi ad un calcolo equivalente internamente ad uno specifico intervallo dove l'algoritmo converge, quindi passare per un'approssimazione di tipo polinomiale oppure di tipo razionale.
NEL PRESENTE
È naturale che il pensiero corra immediatamente alle approssimazioni di Taylor nel caso polinomiale e alle approssimazioni di Padé nel caso razionale, in quanto sono di semplice calcolo e rispetto le quali abbiamo una discreta dimestichezza dovuta al fatto che nell'analisi matematica sono ovunque come il prezzemolo. D'altro canto, tali scelte non sono le migliori possibili in questo ambito, in particolare hanno la meglio i cosiddetti polinomi minimax (o le rispettive approssimazioni razionali). I motivi sono essenzialmente due: a parità di grado offrono un errore massimo inferiore e inoltre l'errore è spalmato uniformemente in un dato intervallo, a differenza dei precedenti che sono ottimi nell'intorno del centro, ma scadenti verso gli estremi dell'intervallo.
L'altra faccia della medaglia, però, è che la determinazione di quei benedetti polinomi minimax non è banale e lo standard al riguardo porta all'algoritmo di Remez, il quale dati in input la funzione elementare e l'intervallo in cui si desidera approssimarla, quindi il grado del polinomio approssimante, tramite un processo iterativo calcola i coefficienti di tale polinomio, che sottostando al teorema dell'equioscillazione ne garantisce l'unicità.
POLINOMI MINIMAX
Un codice piuttosto succinto, seppur non molto robusto, è il seguente:
- Codice:
f[x_] = Sin[x];
{a, b, n} = {-Pi/4, Pi/4, 10};
u = Table[i, {i, a, b, (b - a)/(n + 1)}];
Do[p[x_] = Sum[StringJoin["c", ToString[i]] x^i, {i, 0, n}];
v = Table[p[u[[i]]] - f[u[[i]]] == (-1)^i k, {i, n + 2}];
p[x_] = p[x] /. NSolve[v][[1]];
w = NSolve[{TrigToExp[D[p[x] - f[x], x]] == 0, a < x < b}];
u = Sort@N@Join[{a, b}, w[[All, 1, 2]]], {j, 20}];
Chop@p[x]
Plot[p[x] - f[x], {x, a, b}, AxesLabel -> {"x", "p(x)-f(x)"}]
che lanciato in Wolfram Mathematica sputa quanto segue:
- Codice:
0.999999999976264 x -
0.16666666589651935 x^3 +
0.008333326335356108 x^5 -
0.0001983867334444072 x^7 +
0.000002713535577336344 x^9
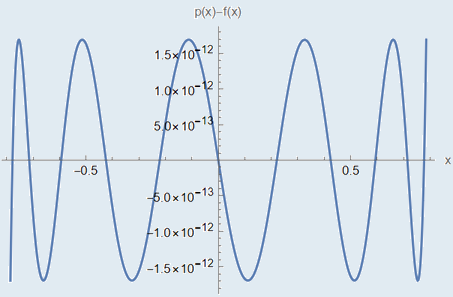
a differenza di quanto si otterrebbe con la rispettiva approssimazione di Taylor:
- Codice:
x -
0.16666666666666666 x^3 +
0.008333333333333333 x^5 -
0.0001984126984126984 x^7 +
0.0000027557319223985893 x^9

FUNZIONI ELEMENTARI PRIMITIVE
Ora abbiamo tutti gli strumenti per scrivere dei "codici giocattolo" circa le funzioni elementari di base:
- Codice:
sin[x_] := Module[{n, pi, y, siny, cosy},
{n, pi, y} = {0, 3.141592653589793, x};
While[y < -pi/4, n = n + 1; y = y + pi/2];
While[y > +pi/4, n = n - 1; y = y - pi/2];
siny = 0.999999999976264 y - 0.16666666589651935 y^3 +
0.008333326335356108 y^5 - 0.0001983867334444072 y^7 +
0.000002713535577336344 y^9;
cosy = 0.9999999999999444 - 0.4999999999935193 y^2 +
0.04166666654402005 y^4 - 0.0013888880398758362 y^6 +
0.000024798929682192885 y^8 - 0.00000027173490012904213 y^10;
If[Mod[n, 4] == 0, siny, If[Mod[n, 4] == 1, -cosy, If[Mod[n, 4] == 2, -siny, cosy]]]]
- Codice:
cos[x_] := Module[{n, pi, y, siny, cosy},
{n, pi, y} = {0, 3.141592653589793, x};
While[y < -pi/4, n = n - 1; y = y + pi/2];
While[y > +pi/4, n = n + 1; y = y - pi/2];
siny = 0.999999999976264 y - 0.16666666589651935 y^3 +
0.008333326335356108 y^5 - 0.0001983867334444072 y^7 +
0.000002713535577336344 y^9;
cosy = 0.9999999999999444 - 0.4999999999935193 y^2 +
0.04166666654402005 y^4 - 0.0013888880398758362 y^6 +
0.000024798929682192885 y^8 - 0.00000027173490012904213 y^10;
If[Mod[n, 4] == 0, cosy, If[Mod[n, 4] == 1, -siny, If[Mod[n, 4] == 2, -cosy, siny]]]]
- Codice:
arctan[x_] := Module[{m, n, pi, y, arctany},
{m, n, pi, y} = {0, 1, 3.141592653589793, x};
If[y < 0, n = -1; y = -x];
If[y > 1, m = 1; y = 1/y];
arctany = 0.9999999146206229 y + 0.000004440916687621521 y^2 -
0.3334229328258918 y^3 + 0.0009160176902325137 y^4 +
0.19467852030293517 y^5 + 0.01810645296260239 y^6 -
0.17583841962361396 y^7 + 0.011728511647071702 y^8 +
0.1956314075888416 y^9 - 0.19507021552110818 y^10 +
0.08234872936245016 y^11 - 0.013684264265137207 y^12;
If[m == 0, n arctany, n (pi/2 - arctany)]]
- Codice:
exp[x_] := Module[{n, log2, y, expy},
{n, log2, y} = {1, 0.6931471805599453, x};
While[y < 0, n = n/2; y = y + log2];
While[y > log2, n = 2 n; y = y - log2];
expy = 0.9999999999999809 + 1.0000000000054843 y +
0.49999999974080833 y^2 + 0.16666667141752853 y^3 +
0.041666622484762016 y^4 + 0.008333568911715338 y^5 +
0.0013881265875033293 y^6 + 0.00019993071014806345 y^7 +
0.00002299592844852003 y^8 + 0.000003910027293592432 y^9;
n expy]
- Codice:
log[x_] := Module[{n, log2, y, logy},
{n, log2, y} = {0, 0.6931471805599453, x};
While[y < 1, n = n - 1; y = 2 y];
While[y > 2, n = n + 1; y = y/2];
logy = -2.758798873492117 + 8.482177884092106 y -
16.404818190077595 y^2 + 25.509315252813245 y^3 -
29.970734938543238 y^4 + 26.57580667306714 y^5 -
17.810152466522702 y^6 + 8.975140918706439 y^7 -
3.350162015718218 y^8 + 0.8989936219430049 y^9 -
0.16408089302388532 y^10 + 0.01824637444011346 y^11 -
0.0009333476666561241 y^12;
n log2 + logy]
FUNZIONI ELEMENTARI DERIVATE
A sua volta, risulta possibile definite tutte le altre funzioni elementari, tra le quali: \[
\begin{aligned}
& \tan(x) = \frac{\sin(x)}{\cos(x)}, \quad
\log_a(x) = \frac{\log(x)}{\log(a)}, \quad
x^y = e^{y\log(x)}, \\
& \text{surd}(x,n) =
\begin{cases}
-(-x)^{\frac{1}{n}} & \text{se} \; x < 0 \, \land \, \text{mod}(n,2) = 1 \\
x^{\frac{1}{n}} & \text{se} \; x > 0 \\
\end{cases}, \\
& \arcsin(x) = \arctan\left(\frac{x}{\left(1-x^2\right)^{\frac{1}{2}}}\right), \quad
\arccos(x) = \frac{\pi}{2} - \arcsin(x), \\
& \sinh(x) = \frac{e^x-e^{-x}}{2}, \quad
\cosh(x) = \frac{e^x+e^{-x}}{2}, \quad
\tanh(x) = \frac{\sinh(x)}{\cosh(x)}, \\
& \text{arcsinh}(x) = \log\left(x+\left(x^2+1\right)^{\frac{1}{2}}\right), \quad
\text{arccosh}(x) = \log\left(x+\left(x^2-1\right)^{\frac{1}{2}}\right), \\
& \text{arctanh}(x) = \frac{\log(1+x)-\log(1-x)}{2}.
\end{aligned}
\]
CONCLUSIONI
Va da sé che tali funzioni siano state implementate in modo molto ingenuo, in particolare ciò può essere visto come un punto di partenza per un'analisi seria, specie nella fase di rimodulazione dell'input in cui per numeri molto grandi può verificarsi una sensibile perdita di precisione, a cui poi andranno affiancati tutta una serie di accorgimenti per fare in modo che eventuali input non consentiti siano immediatamente arrestati e così via.
Con questo io avrei finito lo sproloquio, se a qualcuno facesse piacere aggiungere qualche osservazione o qualche invettiva causa le troppe stupidaggini scritte lo faccia pure, non faranno altro che bene, soprattutto per coloro che un domani dovessero incappare qui tramite i motori di ricerca. Buon Natale a tutti voi!





