Ogni tanto su fb oltre a sistemi lineari con banane e mele che solo 1% della popolazione sa risolvere (con tanto di immagine Einstein "che pensa" per fare sembrare la cosa ancora più difficile...vabbè mi sono dilungato...) ci si può imbattere anche su problemi interessanti come questo...
Siano $\mathbb{N}$ l'insieme degli interi positivi, $G$ un gruppo abeliano finito e
$f:\mathbb{N} \mapsto G$
una funzione tale che
$f(mn) = f(m)f(n)$ per ogni $m$, $n$ naturali.
Dimostrare che esistono infiniti $k$ tali che $f(k)=f(k+1)$.
11 messaggi
• Vai alla pagina... • 1, 2
$f: \mathbb{N} \mapsto G$
"Chi è padrone del proprio respiro, è padrone della propria vita."~ Antico proverbio
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
- dan95
- Cannot live without

- Messaggio: 2494 di 5285
- Iscritto il: 10/06/2013, 16:37
- Località: Roma Caput Mundi
Re: $f: \mathbb{N} \mapsto G$
1. E' facile osservare che \(f\) è un omomorfismo di monoidi \((\mathbb N,\cdot)\to (G,+)\), perché \[f1=f(1\cdot 1)=f1\cdot f1\] sicché \(f1\) è un idempotente in $G$, che siccome è un gruppo non ne ha di non banali.
2. Per la proprietà universale del gruppo di Grothendieck, \(f\) corrisponde a un omomorfismo di gruppi \[\bar f : K(\mathbb N,\cdot) \to G\] dove \(K(\mathbb N,\cdot)\) è appunto il gruppo di Grothendieck di \((\mathbb N,\cdot)\); incidentalmente, questo è il gruppo abeliano dei numeri razionali strettamente positivi, preso rispetto alla moltiplicazione, perché \(f : \mathbb N \to G\) si estende a \(\bar f : (\mathbb Q_{>0}, \cdot) \to G\) mandando \(\frac{m}{n}\) in \(fm-fn\).
3. Per ovvie ragioni di piccionaia, ogni fibra di \(\bar f\) ha cardinalità infinita (è qui che questa dimostrazione usa la commodity di essere passati ai gruppi, perché nei gruppi la cardinalità di una fibra di un omomorfismo \(\varphi\) è decisa dalla cardinalità di \(\ker \varphi\); nei monoidi questo è falso --incidentalmente, questo significa che la categoria dei monoidi non è una varietà di Mal'cev), e questo conclude, perché l'insieme \(\{k\in\mathbb N\mid fk = f(k+1)\}\) è precisamente la fibra di \(\bar f\) sopra \(\frac{k}{k+1}\).
2. Per la proprietà universale del gruppo di Grothendieck, \(f\) corrisponde a un omomorfismo di gruppi \[\bar f : K(\mathbb N,\cdot) \to G\] dove \(K(\mathbb N,\cdot)\) è appunto il gruppo di Grothendieck di \((\mathbb N,\cdot)\); incidentalmente, questo è il gruppo abeliano dei numeri razionali strettamente positivi, preso rispetto alla moltiplicazione, perché \(f : \mathbb N \to G\) si estende a \(\bar f : (\mathbb Q_{>0}, \cdot) \to G\) mandando \(\frac{m}{n}\) in \(fm-fn\).
3. Per ovvie ragioni di piccionaia, ogni fibra di \(\bar f\) ha cardinalità infinita (è qui che questa dimostrazione usa la commodity di essere passati ai gruppi, perché nei gruppi la cardinalità di una fibra di un omomorfismo \(\varphi\) è decisa dalla cardinalità di \(\ker \varphi\); nei monoidi questo è falso --incidentalmente, questo significa che la categoria dei monoidi non è una varietà di Mal'cev), e questo conclude, perché l'insieme \(\{k\in\mathbb N\mid fk = f(k+1)\}\) è precisamente la fibra di \(\bar f\) sopra \(\frac{k}{k+1}\).
-

megas_archon - Senior Member

- Messaggio: 341 di 1341
- Iscritto il: 13/06/2021, 20:57
Re: $f: \mathbb{N} \mapsto G$
Non mi è tanto chiaro perché la fibra di $\bar(f)$ è sopra a $\frac{k}{k+1}$, a me pare sia sopra a $0$
Ultima modifica di dan95 il 18/06/2022, 16:19, modificato 1 volta in totale.
"Chi è padrone del proprio respiro, è padrone della propria vita."~ Antico proverbio
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
- dan95
- Cannot live without

- Messaggio: 2496 di 5285
- Iscritto il: 10/06/2013, 16:37
- Località: Roma Caput Mundi
Re: $f: \mathbb{N} \mapsto G$
$$\bar{f}^{-1}(\{0\})=\{q \in Q^{\ast}| \bar{f}(q)=0\}$$
Che come dici ha cardinalità infinita ma chi mi assicura che $\frac{k}{k+1} \in \bar(f)^{-1}({0})$
Che come dici ha cardinalità infinita ma chi mi assicura che $\frac{k}{k+1} \in \bar(f)^{-1}({0})$
"Chi è padrone del proprio respiro, è padrone della propria vita."~ Antico proverbio
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
- dan95
- Cannot live without

- Messaggio: 2497 di 5285
- Iscritto il: 10/06/2013, 16:37
- Località: Roma Caput Mundi
Re: $f: \mathbb{N} \mapsto G$
gnap. Sì, volevo scrivere che $fk=f(k+1)$ se e solo se \(\frac{k}{k+1}\) sta in \(\ker \bar f\); adesso però per quale motivo ci devono essere infiniti elementi nel nucleo di quella forma? Inizierei dicendo che ci sta 0, per l'ovvio motivo che \(f0=f1=0_G\), e se ora $k$ ci sta, ma c'è un \(k^*\) massimo per cui ci sta... uff, non riesco a farlo a mente. Pazienza, ci ho provato.
-

megas_archon - Senior Member

- Messaggio: 342 di 1341
- Iscritto il: 13/06/2021, 20:57
Re: $f: \mathbb{N} \mapsto G$
megas_archon ha scritto: uff, non riesco a farlo a mente. Pazienza, ci ho provato.
Ecco a che serve risolvere i sistemi lineari con mele e banane
"Chi è padrone del proprio respiro, è padrone della propria vita."~ Antico proverbio
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
- dan95
- Cannot live without

- Messaggio: 2498 di 5285
- Iscritto il: 10/06/2013, 16:37
- Località: Roma Caput Mundi
Re: $f: \mathbb{N} \mapsto G$
Testo nascosto, perché contrassegnato dall'autore come fuori tema. Fai click in quest'area per vederlo.
Metti off-topic sennò magari qualcuno risolve quello invece del problema 
"Chi è padrone del proprio respiro, è padrone della propria vita."~ Antico proverbio
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
- dan95
- Cannot live without

- Messaggio: 2500 di 5285
- Iscritto il: 10/06/2013, 16:37
- Località: Roma Caput Mundi
Re: $f: \mathbb{N} \mapsto G$
Testo nascosto, perché contrassegnato dall'autore come fuori tema. Fai click in quest'area per vederlo.
Oppure:
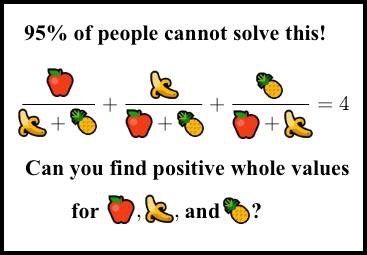
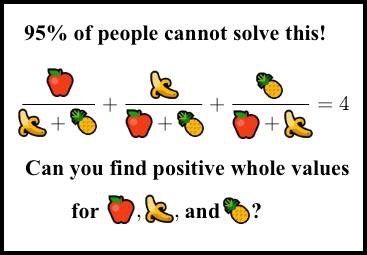
- otta96
- Cannot live without

- Messaggio: 2586 di 5777
- Iscritto il: 12/09/2015, 22:15
Re: $f: \mathbb{N} \mapsto G$
Hint:
Testo nascosto, fai click qui per vederlo
Ogni sottogruppo $S$ di un gruppo abeliano $G$ è normale e per ogni divisore $d$ di $|G|$ esiste un sottogruppo normale di ordine $d$.
"Chi è padrone del proprio respiro, è padrone della propria vita."~ Antico proverbio
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
"La capacità di scegliere è un dono che la natura fa all'uomo. Scegliere è un dono che l'uomo fa a se stesso." D.B.
"Il genio è semplicemente un uomo con la mente da donna." D. B.
- dan95
- Cannot live without

- Messaggio: 2508 di 5285
- Iscritto il: 10/06/2013, 16:37
- Località: Roma Caput Mundi
11 messaggi
• Vai alla pagina... • 1, 2
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite
