Per quali numeri positivi $a$ e $b$, con $a>1$, l'equazione $log_a x = x^b$ ha soluzioni positive per $x$?
Cordialmente, Alex
6 messaggi
• Pagina 1 di 1
Re: Logaritmo e potenza
Onestamente non capisco...
Testo nascosto, fai click qui per vederlo
mi sembra che ci sia sempre una soluzione, che cosa sbaglio ???
- Quinzio
- Cannot live without

- Messaggio: 5670 di 10547
- Iscritto il: 24/08/2010, 06:50
Re: Logaritmo e potenza
Testo nascosto, fai click qui per vederlo
Non ho capito ... intendi dire che qualsiasi coppia $(a,b)$ va bene?
Per esempio $log_2 x = x^3$ non ha soluzioni reali.
Per esempio $log_2 x = x^3$ non ha soluzioni reali.
- axpgn
- Cannot live without

- Messaggio: 21692 di 40678
- Iscritto il: 20/11/2013, 22:03
Re: Logaritmo e potenza
Testo nascosto, fai click qui per vederlo
Dato che: \[
\log_a(x) = x^b
\quad \Rightarrow \quad
\log_a\left(x^b\right) = b\,x^b
\quad \Rightarrow \quad
x^b = a^{b\,x^b}
\quad \Rightarrow \quad
x^b = e^{b\,x^b\log(a)}
\] ossia: \[
x^b e^{-b\,x^b\log(a)} = 1
\quad \Rightarrow \quad
-b\,x^b\log(a)\,e^{-b\,x^b\log(a)} = -b\log(a)
\quad \Rightarrow \quad
y\,e^y = -b\log(a)
\] essendo noto che: \[
y\,e^y \ge -\frac{1}{e} \quad \quad \forall\,y \in \mathbb{R}
\] allora deve essere: \[
\boxed{-b\log(a) \ge -\frac{1}{e}\,}
\] ossia: \[
{\color{blue}{\left(0 < a < 1 \quad \land \quad b \ge \frac{1}{e\log(a)}\right)}}
\quad \vee \quad
{\color{red}{\left(a > 1 \quad \land \quad b \le \frac{1}{e\log(a)}\right)}}
\] \(\quad\quad\quad\quad\)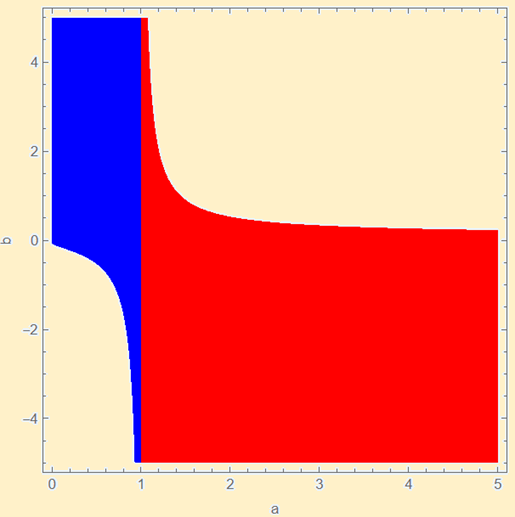
\log_a(x) = x^b
\quad \Rightarrow \quad
\log_a\left(x^b\right) = b\,x^b
\quad \Rightarrow \quad
x^b = a^{b\,x^b}
\quad \Rightarrow \quad
x^b = e^{b\,x^b\log(a)}
\] ossia: \[
x^b e^{-b\,x^b\log(a)} = 1
\quad \Rightarrow \quad
-b\,x^b\log(a)\,e^{-b\,x^b\log(a)} = -b\log(a)
\quad \Rightarrow \quad
y\,e^y = -b\log(a)
\] essendo noto che: \[
y\,e^y \ge -\frac{1}{e} \quad \quad \forall\,y \in \mathbb{R}
\] allora deve essere: \[
\boxed{-b\log(a) \ge -\frac{1}{e}\,}
\] ossia: \[
{\color{blue}{\left(0 < a < 1 \quad \land \quad b \ge \frac{1}{e\log(a)}\right)}}
\quad \vee \quad
{\color{red}{\left(a > 1 \quad \land \quad b \le \frac{1}{e\log(a)}\right)}}
\] \(\quad\quad\quad\quad\)

- sellacollesella
- Average Member

- Messaggio: 495 di 959
- Iscritto il: 08/04/2022, 12:43
Re: Logaritmo e potenza
Testo nascosto, fai click qui per vederlo
Se le due curve
$f(x)= \log_a x$
$g(x) = x^b$
avessero un punto solo di tangenza dovrebbe verificarsi che:
$f(x)=g(x)$
e
$f'(x)=g'(x)$
$f'(x) = 1/(x \ln a)$
$g'(x)= bx^(b-1)$
$1/(x \ln a) = bx^(b-1) -> x = (b \ln a)^(-1/b)$
Poi se $f(x)= g(x)$ cioe'
$\log_a x = x^b$
sostituendo $x$
$-1/b \log_a (b \ln a) = 1/(b \ln a)$
$-\log_a (b \ln a) = 1/ \ln a$
$-(\log_a b + 1) = 1/ \ln a$
$-(\ln b / \ln a + \ln (\ln a) / \ln a) = 1/ \ln a$
$-(\ln b + \ln (\ln a) ) = 1$
$b = 1/(e \ln a)$
Soluzione $b < 1/(e \ln a)$
Un ripassone dei logaritmi !
$f(x)= \log_a x$
$g(x) = x^b$
avessero un punto solo di tangenza dovrebbe verificarsi che:
$f(x)=g(x)$
e
$f'(x)=g'(x)$
$f'(x) = 1/(x \ln a)$
$g'(x)= bx^(b-1)$
$1/(x \ln a) = bx^(b-1) -> x = (b \ln a)^(-1/b)$
Poi se $f(x)= g(x)$ cioe'
$\log_a x = x^b$
sostituendo $x$
$-1/b \log_a (b \ln a) = 1/(b \ln a)$
$-\log_a (b \ln a) = 1/ \ln a$
$-(\log_a b + 1) = 1/ \ln a$
$-(\ln b / \ln a + \ln (\ln a) / \ln a) = 1/ \ln a$
$-(\ln b + \ln (\ln a) ) = 1$
$b = 1/(e \ln a)$
Soluzione $b < 1/(e \ln a)$
Un ripassone dei logaritmi !
- Quinzio
- Cannot live without

- Messaggio: 5675 di 10547
- Iscritto il: 24/08/2010, 06:50
Re: Logaritmo e potenza
Bravi! 

Testo nascosto, fai click qui per vederlo
Eh, beh ... però mi piace di più scritta così $1<a<e^(1/(be))$ 

- axpgn
- Cannot live without

- Messaggio: 21696 di 40678
- Iscritto il: 20/11/2013, 22:03
6 messaggi
• Pagina 1 di 1
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite