Massimo di due variabili aleatorie uniformi

[RuCoLa]

Buongiorno a tutti,
in questo esercizio è richiesto di calcolare la funzione di distribuzione della seguente variabile aleatoria $Z = max(X,Y)$ dove $X in U(0,1), Y in U(0,2)$ e $X,Y$ sono indipendenti. La strada più breve per risolvere l'esercizio credo sia la seguente: $F_z(\alpha)= P(Z<= \alpha) = P(max(X,Y)<=\alpha) = P(X<=\alpha,Y<=\alpha) = P(X<=\alpha)*P(Y<=\alpha)$.
Volevo provare un approccio alternativo facendo le seguenti considerazioni: una partizione di $RR^2$ è $X>=Y uu X<Y$, e sfruttando il teorema della probabilità totale $P(max(X,Y)<=\alpha) = P(max(X,Y)<=\alpha nn (X>=Y uu X<Y)) = P(max(X,Y)<=\alpha | X>=Y) *P(X>=Y) + P(max(X,Y)<=\alpha | X<Y)*P(X<Y) = P(X <=\alpha | X>=Y) *P(X>=Y) + P(Y<=\alpha | X<Y)*P(X<Y) =^(???) P(X <=\alpha) *P(X>=Y) + P(Y<=\alpha)*P(X<Y)$
Non sono sicuro dell'ultima uguaglianza, ma la giustificherei con il fatto che $X,Y$ sono indipendenti...In realtà il risultato che si ottiene non coincide con quello ottenuto con la strada più breve ma non ne capisco il motivo.Concettualmente la logica di questa seconda strada sarebbe questa: ho provato a disegnare il piano cartesiano(Y ordinate,X ascisse) e dividerlo in due semipiani con la retta $Y = X$. Nel semipiano al di sopra della retta si ha $ Z = Y$, al di sotto $Z = X$. A questo punto per calcolare la $P(Z<\alpha)$ calcolo la probabilità che $Z = Y$ e la moltiplico per la probabilità che $Y <= \alpha$, stesso discorso per $Z = X$ e infine sommo i due risultati, ottenendo la formula che ho scritto dopo i tre punti interrogativi. Potete spiegarmi perchè questa seconda strada è sbagliata? (Probabilmente l'evento $X<=\alpha$ non è indipendente da $X>=Y$ ma non me lo spiego)

Grazie

[tommik]

Si può fare in entrambi i modi, dato che la seconda via è semplicemente la disintegrazione della prima¹. Per non sbagliare penso convenga ribaltare gli eventi nel seguente modo²

$F_Z(z)=mathbb{P}(X<z)mathbb{P}(X>Y|X<z)+mathbb{P}(Y<z)mathbb{P}(Y>X|Y<z)$

Ovviamente tali probabilità cambiano al variare di $Z$ nel suo dominio.

Es, per $z in [1;2)$ ottieni

$F_Z(z)=1xx0+z/2xx1=z/2$

In definitiva, trovi

$F_Z(z)={{: ( 0 , ;z<0 ),( z^2/2 , ;0<=z<1),( z/2 , ;1<=z<2 ),( 1, ;z>=2 ) :}$

Come deve essere!

Per vedere se hai capito (non è necessario postare la soluzione) puoi provare questo (inventato or ora...)

Siano $X,Y$ variabili aleatorie indipendenti con legge $X~U(0;3)$; $Y~"Binomiale"(1;1/6)$

Calcolare la legge di $Z=min(X,Y)$

---

Note

1. ...e non sono le uniche vie risolutive. Se vuoi utilizzare approcci alternativi interessanti prova con le Statistiche d'ordine oppure puoi guardare Questo esempio ↑
2. uso le disuguaglianze forti per semplificare la notazione tanto nulla cambia essendo $mathbb{P}[X=Y]=0$ ↑

[RuCoLa]

Grazie per la dritta. Non sono ancora molto esperto sul tema ma in che modo posso calcolare, per esempio, il termine $P(X>Y|X<z)$? Se dovessi ricorrere alla formula $P(X>Y|X<z) = (P(X>Y,X<z))/(P(X<z))$ e calcolare il numeratore con $\int_(-oo)^z \int_(-oo)^x f_(X,Y)(x,y)dydx$ di fatto non avrei guadagnato nulla nello scrivere $P(X<z)P(X>Y|X<z)$ piuttosto che $P(X>Y,X<z)$.

Testo nascosto, fai click qui per vederlo

la soluzione all'esercizio mi viene $F_Z(z) = \{(0 ;z<0),((5+z/3)/6 ; 0<=z<1),(1 ;z>=1):}$

[tommik]

Le variabili sono uniformi, ergo l'integrale non serve. Il modo più immediato è quello di calcolare direttamente la probabilità congiunta: l'area del triangolino colorato moltiplicata per la densità congiunta




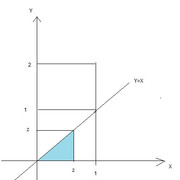
$z^2/2*1/2$

Ragionando così (ecco un altro modo di risolvere il problema) trovi immediatamente anche la funzione di distribuzione del massimo per l'intervallo $z in [0;1]$...è l'area del quadrato di lato $z$ moltiplicata per la densità congiunta: $F_Z=z^2/2$

io i conti dell'esercizio li ho fatti a mente con alcune semplici considerazioni, ma l'importante è arrivare al risultato corretto.

L'esercizio che ti ho proposto è stato svolto correttamente. Direi che ci siamo, hai trovato una densità mista ...puoi passare oltre, IMHO

EDIT:
tra l'altro l'esercizio che ti ho proposto lo hai risolto perfettamente. Hai anche azzeccato per bene gli intervalli. Nota che ci sono due punti di discontinuità nella funzione di distribuzione. In quei punti la densità non è continua ma concentra massa di probabilità positiva

$mathbb{P}(Z=0)=5/6$

$mathbb{P}(Z=1)=1/9$

[RuCoLa]

Va bene, grazie!!