Dato un triangolo acutangolo, qual è il triangolo inscritto in esso dal minor perimetro?
Dimostrazione.
Cordialmente, Alex
19 messaggi
• Vai alla pagina... • 1, 2
Re: Triangolo nel triangolo
Mando la mia risposta, anche se la parte finale della dimostrazione mi piace poco.
Testo nascosto, fai click qui per vederlo
Il perimetro minore si ottiene congiungendo i piedi delle altezze.
Figura: $ABC$ è il triangolo dato; $DEF$ è quello interno (con D su AB, E su BC, F su CA); $D_1, D_2$ sono i simmetrici di D rispetto ad AC,BC; $M$ è il punto medio di $D_1D_2$.
Dimostrazione: si ha $DF=D_1F$ e $DE=ED_2$, quindi il perimetro è uguale alla spezzata $D_1EFD_2$ ed è minimo quando la spezzata diventa il segmento $D_1D_2$.
Resta da determinare la miglior posizione di D. Notiamo che per le simmetrie si ha $CD_1=CD$ e $CD_2=CD$, quindi il triangolo $CD_1D_2$ è isoscele e $CD_1M$ è la sua metà, rettangolo.
Sempre per le simmetrie, si ha
${(D_1 hatCD=2A hatCD),(D hatCD_2=2DhatCB):}-> D_1 hatCD_2=2(AhatCD+DhatCB)=2 gamma->D_1hatCM=gamma$
Da quanto detto consegue
$D_1D_2=2D_1M=2CD_1 sin gamma=2 CD sin gamma$
che è minimo quando lo è CD, cioè quando D è il piede dell'altezza relativa ad AB.
Ragionando analogamente, si trova che affermazioni simili valgono anche per E,F e quindi vale la mia risposta.
Trovo però poco convincente l'ultima frase scritta (e se ci fossero tre soluzioni distinte?) e per questo aprirò un altro post, che penso di intitolare "Piedi delle altezze", sperando che qualcuno la migliori. Per ora, riesco solo a dimostrare che
$"perimetro minimo"=(2S)/R$
con la solita simbologia (S è l'area di ABC ed R è il raggio del cerchio circoscritto).
Figura: $ABC$ è il triangolo dato; $DEF$ è quello interno (con D su AB, E su BC, F su CA); $D_1, D_2$ sono i simmetrici di D rispetto ad AC,BC; $M$ è il punto medio di $D_1D_2$.
Dimostrazione: si ha $DF=D_1F$ e $DE=ED_2$, quindi il perimetro è uguale alla spezzata $D_1EFD_2$ ed è minimo quando la spezzata diventa il segmento $D_1D_2$.
Resta da determinare la miglior posizione di D. Notiamo che per le simmetrie si ha $CD_1=CD$ e $CD_2=CD$, quindi il triangolo $CD_1D_2$ è isoscele e $CD_1M$ è la sua metà, rettangolo.
Sempre per le simmetrie, si ha
${(D_1 hatCD=2A hatCD),(D hatCD_2=2DhatCB):}-> D_1 hatCD_2=2(AhatCD+DhatCB)=2 gamma->D_1hatCM=gamma$
Da quanto detto consegue
$D_1D_2=2D_1M=2CD_1 sin gamma=2 CD sin gamma$
che è minimo quando lo è CD, cioè quando D è il piede dell'altezza relativa ad AB.
Ragionando analogamente, si trova che affermazioni simili valgono anche per E,F e quindi vale la mia risposta.
Trovo però poco convincente l'ultima frase scritta (e se ci fossero tre soluzioni distinte?) e per questo aprirò un altro post, che penso di intitolare "Piedi delle altezze", sperando che qualcuno la migliori. Per ora, riesco solo a dimostrare che
$"perimetro minimo"=(2S)/R$
con la solita simbologia (S è l'area di ABC ed R è il raggio del cerchio circoscritto).
- Indicando i metri con m e i centimetri con cm, si ha m=100 cm. Quindi 5 centimetri equivalgono a metri m=100*5=500.
- E' disonesto che un disonesto si comporti in modo onesto (R. Powell)
- E' disonesto che un disonesto si comporti in modo onesto (R. Powell)
- giammaria
- Cannot live without

- Messaggio: 5109 di 9472
- Iscritto il: 29/12/2008, 22:19
- Località: provincia di Asti
Re: Triangolo nel triangolo
Conosco due dimostrazioni del perché quello individuato da giammaria è il triangolo inscritto di minor perimetro.
Una è impostata come quella di giammaria ma si conclude diversamente ed entrambe fanno uso solo della geometria sintetica.
Cordialmente, Alex
Una è impostata come quella di giammaria ma si conclude diversamente ed entrambe fanno uso solo della geometria sintetica.
Cordialmente, Alex
- axpgn
- Cannot live without

- Messaggio: 14329 di 40677
- Iscritto il: 20/11/2013, 22:03
Re: Triangolo nel triangolo
Ecco la prima (che poi, cronologicamente, sarebbe la seconda  ), non fa uso della trigonometria, solo sintetica (la geometria non la dimostrazione
), non fa uso della trigonometria, solo sintetica (la geometria non la dimostrazione  )
)
Cordialmente, Alex
 )
)Testo nascosto, fai click qui per vederlo
- triangolo acutangolo $ABC$
- triangolo arbitrario $UVW$ inscritto in $ABC$ con $U$ su $BC$, $V$ su $CA$ e $W$ su $AB$.
- siano $U'$ e $U''$ i simmetrici di $U$ rispetto ad $AC$ e ad $AB$.
- il perimetro del triangolo $UVW$ è pari alla spezzata $U'VWU''$
- tenendo fisso $U$, rimangono fissi pure $U'$ e $U''$, pur spostando $V$ e $W$
- il percorso più breve da $U'$ a $U''$ è la retta quindi la spezzata $U'VWU''$ sarà la più corta quando $V$ e $W$ si troveranno sul segmento $U'U''$
- conseguentemente il segmento $U'U''$ è il minor perimetro possibile per un triangolo inscritto in $ABC$ con un vertice in $U$
Adesso va trovato il punto $U$ che renda "minimo" questo triangolo
- il triangolo $AU'U''$ è isoscele e la lunghezza dei suoi lati obliqui dipendono dalla lunghezza di $AU$
- invece l'angolo $U'AU''$ non dipende dalla posizione di $U$ ma solo dal triangolo $ABC$, quindi la sua ampiezza è costante
- il nostro obiettivo è trovare il minimo $U'U''$
- dato che l'angolo $U'AU''$ non dipende da $U$, tra tutti i triangoli $AU'U''$ quello con la base minore avrà anche i lati minori
- ma i lati sono uguali ad $AU=AU'=AU''$ quindi dobbiamo cercare il segmento $AU$ più corto
- e questo lo avremo quando $AU$ è l'altezza di $ABC$ rispetto a $BC$
Ricapitolando abbiamo dimostrato che il triangolo con il minor perimetro è quello costruito in questo modo con $U$ piede dell'altezza.
Lo stessa costruzione possiamo rifarla sugli altri due lati.
Quindi il triangolo inscritto con il minor perimetro è quello con vertici i piedi delle tre altezze.
- triangolo arbitrario $UVW$ inscritto in $ABC$ con $U$ su $BC$, $V$ su $CA$ e $W$ su $AB$.
- siano $U'$ e $U''$ i simmetrici di $U$ rispetto ad $AC$ e ad $AB$.
- il perimetro del triangolo $UVW$ è pari alla spezzata $U'VWU''$
- tenendo fisso $U$, rimangono fissi pure $U'$ e $U''$, pur spostando $V$ e $W$
- il percorso più breve da $U'$ a $U''$ è la retta quindi la spezzata $U'VWU''$ sarà la più corta quando $V$ e $W$ si troveranno sul segmento $U'U''$
- conseguentemente il segmento $U'U''$ è il minor perimetro possibile per un triangolo inscritto in $ABC$ con un vertice in $U$
Adesso va trovato il punto $U$ che renda "minimo" questo triangolo
- il triangolo $AU'U''$ è isoscele e la lunghezza dei suoi lati obliqui dipendono dalla lunghezza di $AU$
- invece l'angolo $U'AU''$ non dipende dalla posizione di $U$ ma solo dal triangolo $ABC$, quindi la sua ampiezza è costante
- il nostro obiettivo è trovare il minimo $U'U''$
- dato che l'angolo $U'AU''$ non dipende da $U$, tra tutti i triangoli $AU'U''$ quello con la base minore avrà anche i lati minori
- ma i lati sono uguali ad $AU=AU'=AU''$ quindi dobbiamo cercare il segmento $AU$ più corto
- e questo lo avremo quando $AU$ è l'altezza di $ABC$ rispetto a $BC$
Ricapitolando abbiamo dimostrato che il triangolo con il minor perimetro è quello costruito in questo modo con $U$ piede dell'altezza.
Lo stessa costruzione possiamo rifarla sugli altri due lati.
Quindi il triangolo inscritto con il minor perimetro è quello con vertici i piedi delle tre altezze.
Cordialmente, Alex
- axpgn
- Cannot live without

- Messaggio: 14348 di 40677
- Iscritto il: 20/11/2013, 22:03
Re: Triangolo nel triangolo
Aggiungo una precisazione …
Cordialmente, Alex
Testo nascosto, fai click qui per vederlo
Dalla dimostrazione precedente forse non è chiaro perché il triangolo inscritto costruito in quel modo è unico.
Provo a dettagliare meglio.
Costruiamo il triangolo "minimo" con le "istruzioni" del post precedente.
Abbiamo il triangolo acutangolo $ABC$ in cui inscriviamo il triangolo "minimo" $EFG$ in questo modo:
Sia $E$ il piede dell'altezza da $A$ su $BC$.
Siano $E'$ ed $E''$ i simmetrici di $E$ rispetto ad $AC$ e ad $AB$.
Quindi il segmento $E'E''$ è la lunghezza del perimetro minimo.
I due punti $F$ e $G$ sono le intersezioni di $E'E''$ con $AC$ e $AB$.
Inscriviamo in $ABC$ un qualsiasi triangolo $UVW$ diverso da $EFG$, con $U$ su $BC$, $V$ su $AC$ e $W$ su $AB$.
Per quanto dimostrato precedentemente, se $U$ è diverso da $E$ allora il segmento $U'U''$ sarà più lungo di $E'E''$ e quindi il perimetro di $UVW$ sarà maggiore; se invece $U$ ed $E$ coincidessero allora almeno uno tra $V$ e $W$ non coinciderà con $F$ e con $G$, di conseguenza la spezzata $E'VWE''$ sarà più lunga del segmento $E'E''$ ed anche in questo caso il triangolo $UVW$ avrà un perimetro maggiore di $EFG$.
Quindi esiste un solo triangolo che ha il perimetro minore di tutti quelli inscrivibili.
Ora questa costruzione parte da UN solo piede di altezza ($E$) mentre di $F$ e $G$ non sappiamo niente.
Ma questa costruzione è replicabile su entrambi gli altri due lati ovvero partendo dagli altri due piedi di altezza e siccome il triangolo "minimo" è unico allora non potrà che essere quello che si ottiene collegando i tre piedi della altezze.
Provo a dettagliare meglio.
Costruiamo il triangolo "minimo" con le "istruzioni" del post precedente.
Abbiamo il triangolo acutangolo $ABC$ in cui inscriviamo il triangolo "minimo" $EFG$ in questo modo:
Sia $E$ il piede dell'altezza da $A$ su $BC$.
Siano $E'$ ed $E''$ i simmetrici di $E$ rispetto ad $AC$ e ad $AB$.
Quindi il segmento $E'E''$ è la lunghezza del perimetro minimo.
I due punti $F$ e $G$ sono le intersezioni di $E'E''$ con $AC$ e $AB$.
Inscriviamo in $ABC$ un qualsiasi triangolo $UVW$ diverso da $EFG$, con $U$ su $BC$, $V$ su $AC$ e $W$ su $AB$.
Per quanto dimostrato precedentemente, se $U$ è diverso da $E$ allora il segmento $U'U''$ sarà più lungo di $E'E''$ e quindi il perimetro di $UVW$ sarà maggiore; se invece $U$ ed $E$ coincidessero allora almeno uno tra $V$ e $W$ non coinciderà con $F$ e con $G$, di conseguenza la spezzata $E'VWE''$ sarà più lunga del segmento $E'E''$ ed anche in questo caso il triangolo $UVW$ avrà un perimetro maggiore di $EFG$.
Quindi esiste un solo triangolo che ha il perimetro minore di tutti quelli inscrivibili.
Ora questa costruzione parte da UN solo piede di altezza ($E$) mentre di $F$ e $G$ non sappiamo niente.
Ma questa costruzione è replicabile su entrambi gli altri due lati ovvero partendo dagli altri due piedi di altezza e siccome il triangolo "minimo" è unico allora non potrà che essere quello che si ottiene collegando i tre piedi della altezze.
Cordialmente, Alex
- axpgn
- Cannot live without

- Messaggio: 14352 di 40677
- Iscritto il: 20/11/2013, 22:03
Re: Triangolo nel triangolo
Ecco la seconda dimostrazione ...
Cordialmente, Alex
Testo nascosto, fai click qui per vederlo
- triangolo acutangolo $ABC$
- triangolo $EFG$ inscritto in $ABC$ formato unendo i piedi delle tre altezze, con $E$ su $BC$, $F$ su $AC$ e $G$ su $AB$.
- generico triangolo $UVW$ inscritto in $ABC$ con $U$ su $BC$, $V$ su $AC$ e $W$ su $AB$.
*** gli angoli $AFG$ e $CFE$ sono uguali.
Partendo dal triangolo $ABC$, lo ribaltiamo (con tutto il suo contenuto cioè i due triangoli inscritti) lungo il lato $BC$ ed otteniamo il triangolo $CBA'$.
Ripetiamo l'operazione sul lato $CA'$ per ottenere $CA'B'$ e poi ancora lungo $B'A'$ (da cui $A'B'C'$) e di nuovo in $B'C'$, poi in $A''C'$ ed infine lungo $A''B''$ per ottenere il triangolo $A''B''C''$.
Di fatto il triangolo $ABC$ si è spostato in $A''B''C''$ parallelamente a sè stesso senza ruotare (o meglio è ruotato di 360°). Conseguentemente $BC$ è paralello a $B''C''$.
Usando la proprietà *** notiamo che la "seconda posizione" di $EG$ (cioè $EG'$) forma un segmento rettilineo con la prima posizione di $EF$. Allo stesso modo notiamo che un lato del nostro triangolo minimo è sempre allineato con questo segmento.
Ovvero il segmento "diritto" $E''E$ è formato da sei segmenti (due $FG$, due $GE$, due $EF$) cioè il doppio del perimetro del triangolo "minimo" mentre la spezzata $UV'W'U'V''W''U''$ è pari al doppio del perimetro del triangolo $UVW$.
Sappiamo già che i segmenti $UE$ e $U''E''$ sono paralleli, inoltre sono uguali perchè corrispondono agli stessi punti del triangolo $ABC$.
Di conseguenza $E''U''UE$ è un paralellogramma e quindi $E''E=U''U$ cioè $UU''$ è lungo come il perimetro del triangolo "minimo" ma è più corto della spezzata che connette $U$ con $U''$ che è pari al perimetro del triangolo generico $UVW$.
In conclusione il perimetro di $EFG$ è minore di quello di qualsiasi altro triangolo inscritto in $ABC$
- triangolo $EFG$ inscritto in $ABC$ formato unendo i piedi delle tre altezze, con $E$ su $BC$, $F$ su $AC$ e $G$ su $AB$.
- generico triangolo $UVW$ inscritto in $ABC$ con $U$ su $BC$, $V$ su $AC$ e $W$ su $AB$.
*** gli angoli $AFG$ e $CFE$ sono uguali.
Testo nascosto, perché contrassegnato dall'autore come fuori tema. Fai click in quest'area per vederlo.
Dimostrazione:
Detto $O$ l'ortocentro di $ABC$, i punti $A, O, F, G$ si trovano tutti sulla circonferenza di diametro $AO$ (perchè $AGO$ e $AFO$ sono triangoli rettangoli), così come i punti $C, O, F, E$ si trovano tutti sulla circonferenza di diametro $CO$.
L'angolo $AFO$ insiste sull'arco $AG$ così come l'angolo $AOG$ perciò essi sono uguali; allo stesso modo accade per gli angoli $CFE$ e $COE$:; ma gli angoli $AOG$ e $COE$ sono opposti al vertice e quindi uguali.
In conclusione $AFG=CFE$.
Lo stesso avviene agli altri due vertici del triangolo $EFG$.
Detto $O$ l'ortocentro di $ABC$, i punti $A, O, F, G$ si trovano tutti sulla circonferenza di diametro $AO$ (perchè $AGO$ e $AFO$ sono triangoli rettangoli), così come i punti $C, O, F, E$ si trovano tutti sulla circonferenza di diametro $CO$.
L'angolo $AFO$ insiste sull'arco $AG$ così come l'angolo $AOG$ perciò essi sono uguali; allo stesso modo accade per gli angoli $CFE$ e $COE$:; ma gli angoli $AOG$ e $COE$ sono opposti al vertice e quindi uguali.
In conclusione $AFG=CFE$.
Lo stesso avviene agli altri due vertici del triangolo $EFG$.
Partendo dal triangolo $ABC$, lo ribaltiamo (con tutto il suo contenuto cioè i due triangoli inscritti) lungo il lato $BC$ ed otteniamo il triangolo $CBA'$.
Ripetiamo l'operazione sul lato $CA'$ per ottenere $CA'B'$ e poi ancora lungo $B'A'$ (da cui $A'B'C'$) e di nuovo in $B'C'$, poi in $A''C'$ ed infine lungo $A''B''$ per ottenere il triangolo $A''B''C''$.
Di fatto il triangolo $ABC$ si è spostato in $A''B''C''$ parallelamente a sè stesso senza ruotare (o meglio è ruotato di 360°). Conseguentemente $BC$ è paralello a $B''C''$.
Usando la proprietà *** notiamo che la "seconda posizione" di $EG$ (cioè $EG'$) forma un segmento rettilineo con la prima posizione di $EF$. Allo stesso modo notiamo che un lato del nostro triangolo minimo è sempre allineato con questo segmento.
Ovvero il segmento "diritto" $E''E$ è formato da sei segmenti (due $FG$, due $GE$, due $EF$) cioè il doppio del perimetro del triangolo "minimo" mentre la spezzata $UV'W'U'V''W''U''$ è pari al doppio del perimetro del triangolo $UVW$.
Sappiamo già che i segmenti $UE$ e $U''E''$ sono paralleli, inoltre sono uguali perchè corrispondono agli stessi punti del triangolo $ABC$.
Di conseguenza $E''U''UE$ è un paralellogramma e quindi $E''E=U''U$ cioè $UU''$ è lungo come il perimetro del triangolo "minimo" ma è più corto della spezzata che connette $U$ con $U''$ che è pari al perimetro del triangolo generico $UVW$.
In conclusione il perimetro di $EFG$ è minore di quello di qualsiasi altro triangolo inscritto in $ABC$
Cordialmente, Alex
- axpgn
- Cannot live without

- Messaggio: 14383 di 40677
- Iscritto il: 20/11/2013, 22:03
Re: Triangolo nel triangolo
Ciao Alex e ciao Giammaria.
Questo quiz (che solo ora vedo qui) è passato in questi giorni in "Rudi Mathematici" (sezione di Coelestis, forum degli astronomi dilettanti).
Io ho trovato una soluzione che mi piace molto e cnsidero originale
e cnsidero originale  .
.
Il percoso su cui procede parte da una banale considerazione di meccanica. Ed è perciò che mi piace e la trovo originale!
________


Questo quiz (che solo ora vedo qui) è passato in questi giorni in "Rudi Mathematici" (sezione di Coelestis, forum degli astronomi dilettanti).
Io ho trovato una soluzione che mi piace molto
 e cnsidero originale
e cnsidero originale  .
.Il percoso su cui procede parte da una banale considerazione di meccanica. Ed è perciò che mi piace e la trovo originale!
Testo nascosto, fai click qui per vederlo
Immaginiamo che il dato triangolo di vertici A, B e C sia materiale, rigido ma anche apribile per poterlo concatenare con un altro aggeggio topologicamente pure "anulare", ossia concatenabile col triangolo come due anelli consecutivi di una catena. Allora: apriamo il triangolo acutangolo e con la spezzata ottenuta infiliamo un elastico anulare (come una fettuccia di cameradaria di bicicletta) di circonferenza decisamente inferiore al perimetro del triangolo.
Poi chiudiamo il triangolo. Ora l'elastico è inanellato col triangolo. Allora mettiamo in tensione l'elastico tenendone un estremo mentre l'altro è al centro di un lato in direzione perpendicolare a questo lato ... e poi agganciamo l'estremo che abbiamo in mano all'angolo opposto di questo lato (come una specie di collana!). Più sottop ho messo una figura che spero renda bene l'idea dell'elastico in tensione agganciato ai lati del triangolo rigido. E supponiamo che il triangolo rigido e l'elastico siano lubrificati in modo che l'elastico possa strisciare sui lati del triangolo senza incontrare attrito.. Allora l'elastico si colloca spontaneamente nella posizione di equilibrio stabile, ossia in un minimo di energia elastica e quindi con la minore lunghezza possibile (dipendente esclusivamente dalla forma del triangolo acutangolo rigido)
Allora succede che
a) L'elastico viene a formare un triangolo inscritto in quello acutangolo rigido:
b) La tensione che allunga l'elastico ha lo stesso modulo in ciascuno dei tre lati (dato che non c'è attrito nelle pieghe dell'elastico a ridsso dei lati del triangolo rigido).
c) Due lati del triangolo-elastico hanno la medesima inclinazione sul lato sul quale hanno un estremo in comune perché se così non fosse le componenti della tensione dei due lati nella direzione del lato del triangolo rigido non sarebbero uguali e l'elastico non sarebbe in equilibrio per cui la piega si sposterebbe fino a ripristinare la posizione di uguale inclinazione dei due lati dell'elastico.
Un piccolo esame sugli angoli di uguale inclinazione porta alla conclusione che nella piega dell'elastico a ridosso di un certo lato del triangolo rigido, le inclinazioni su quel latio dei due lati dell'elastico sono uguali all'angolo opposto a quel lato del triangolo rigido. E alla fine a concludere che dei quattro triangolini che son venuti a formarsi tre – quello centrale costituito dall'elastico escluso – sono simili al triangolo rigido.
Allora si possono scrivere proporzioni in numero sufficiente a calcolare le lunghezze di ttutti i 9 segmenti.
Ho disegnato una figura che intende mostrare il triangolo a perimetro minimo costituito da un elastico che si dispone spontaneamente nella posizione giusta. La figura può essere di riferimento per calcolare il perimetro del triangolo
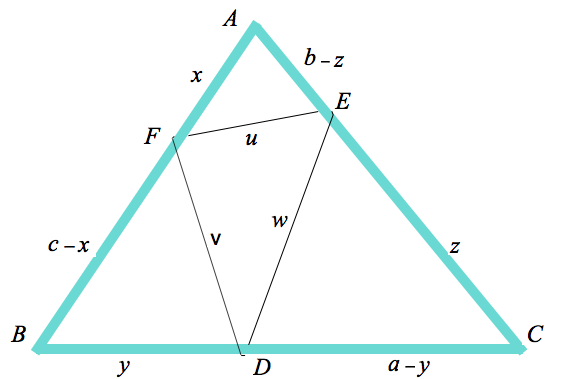
Se a, b e c sono le lunghezze dei lati del triangolo rigid ABC rispettivamente opposti ai verici A, B e C, i coseni degli angoli di vertice rispettivo A, B e C valgono
$cos(α) = (b^2 + c^2 - a^2)/(2bc)$;
$cos(β) = (c^2 + a^2 - b^2)/(2ca)$;
$cos(γ) = (a^2 + b^2 - c^2)/(2ab)$.
Con ciò le lunghezze dei lati del triangolo inscritto a perimetro minimo risultano
$u = a·cos(α)$:
$v = b·cos(β)$;
$w = c·cos(γ)$.
Con i simboli della figura qui sopra, se diciam $r$ il raggio del cerchi inscritto in ABC e diciamo $R$ il raggio del cerchio circoscritto ad ABC tteniamo l'uguaglianza:
$ (u +v + w)/(a + b + c) = r/R$,
Poi chiudiamo il triangolo. Ora l'elastico è inanellato col triangolo. Allora mettiamo in tensione l'elastico tenendone un estremo mentre l'altro è al centro di un lato in direzione perpendicolare a questo lato ... e poi agganciamo l'estremo che abbiamo in mano all'angolo opposto di questo lato (come una specie di collana!). Più sottop ho messo una figura che spero renda bene l'idea dell'elastico in tensione agganciato ai lati del triangolo rigido. E supponiamo che il triangolo rigido e l'elastico siano lubrificati in modo che l'elastico possa strisciare sui lati del triangolo senza incontrare attrito.. Allora l'elastico si colloca spontaneamente nella posizione di equilibrio stabile, ossia in un minimo di energia elastica e quindi con la minore lunghezza possibile (dipendente esclusivamente dalla forma del triangolo acutangolo rigido)
Allora succede che
a) L'elastico viene a formare un triangolo inscritto in quello acutangolo rigido:
b) La tensione che allunga l'elastico ha lo stesso modulo in ciascuno dei tre lati (dato che non c'è attrito nelle pieghe dell'elastico a ridsso dei lati del triangolo rigido).
c) Due lati del triangolo-elastico hanno la medesima inclinazione sul lato sul quale hanno un estremo in comune perché se così non fosse le componenti della tensione dei due lati nella direzione del lato del triangolo rigido non sarebbero uguali e l'elastico non sarebbe in equilibrio per cui la piega si sposterebbe fino a ripristinare la posizione di uguale inclinazione dei due lati dell'elastico.
Un piccolo esame sugli angoli di uguale inclinazione porta alla conclusione che nella piega dell'elastico a ridosso di un certo lato del triangolo rigido, le inclinazioni su quel latio dei due lati dell'elastico sono uguali all'angolo opposto a quel lato del triangolo rigido. E alla fine a concludere che dei quattro triangolini che son venuti a formarsi tre – quello centrale costituito dall'elastico escluso – sono simili al triangolo rigido.
Allora si possono scrivere proporzioni in numero sufficiente a calcolare le lunghezze di ttutti i 9 segmenti.
Ho disegnato una figura che intende mostrare il triangolo a perimetro minimo costituito da un elastico che si dispone spontaneamente nella posizione giusta. La figura può essere di riferimento per calcolare il perimetro del triangolo

Se a, b e c sono le lunghezze dei lati del triangolo rigid ABC rispettivamente opposti ai verici A, B e C, i coseni degli angoli di vertice rispettivo A, B e C valgono
$cos(α) = (b^2 + c^2 - a^2)/(2bc)$;
$cos(β) = (c^2 + a^2 - b^2)/(2ca)$;
$cos(γ) = (a^2 + b^2 - c^2)/(2ab)$.
Con ciò le lunghezze dei lati del triangolo inscritto a perimetro minimo risultano
$u = a·cos(α)$:
$v = b·cos(β)$;
$w = c·cos(γ)$.
Con i simboli della figura qui sopra, se diciam $r$ il raggio del cerchi inscritto in ABC e diciamo $R$ il raggio del cerchio circoscritto ad ABC tteniamo l'uguaglianza:
$ (u +v + w)/(a + b + c) = r/R$,
________


Ultima modifica di Erasmus_First il 10/11/2019, 00:20, modificato 2 volte in totale.
-

Erasmus_First - Senior Member

- Messaggio: 879 di 1805
- Iscritto il: 11/12/2014, 11:41
Re: Triangolo nel triangolo
@Erasmus_First
Prima di tutto, metti i dollari al posto giusto altrimenti non si capisce il finale …
Poi vedo che i nostri problemini piacciono anche altrove …
Che ne pensi invece delle soluzioni che abbiamo scritto?
Cordialmente, Alex
Prima di tutto, metti i dollari al posto giusto altrimenti non si capisce il finale …
Poi vedo che i nostri problemini piacciono anche altrove …
Testo nascosto, fai click qui per vederlo
Mi pare che la tua idea sia, in un certo qual modo, analoga a quella su cui si basa la seconda soluzione che ho postato … d'altra parte mi sembra che tu ti "limiti" a calcolare il perimetro minimo senza però dire qual è il triangolo inscritto dal perimetro minimo che è la cosa più importante ... IMHO
Che ne pensi invece delle soluzioni che abbiamo scritto?
Cordialmente, Alex
- axpgn
- Cannot live without

- Messaggio: 14417 di 40677
- Iscritto il: 20/11/2013, 22:03
Re: Triangolo nel triangolo
Ho corretto i "dollari".  (editando apposta).
(editando apposta).
Ma mi pare che è prroprio questo il bello della mia soluzione!
Trovo infatti le lunghezze dei lati del triangolino ignorando dove stanno i vertici (i quali vanno a posizionarsi "spontaneamente" dove la tensione dell'elasstico viene ad essere la minima possibile
Ma ho altro da ridire a riguardo di questa tua critica (pardon; tuo giusto rilievio] ... e lo metto dentro a "spoiler".
________


 (editando apposta).
(editando apposta).Non èvero che "mi limito a calcolare il perimetro minimo" ma è vero che non dico quall è il triangolo inscritto con tale perimetro, (cioè non dico dove stanno i suoi vertici sui lati del dato triangolo [acutangolo] .axpgn ha scritto:@Erasmus_First
[...] tu ti "limiti" a calcolare il perimetro minimo senza però dire qual è il triangolo inscritto dal perimetro
Ma mi pare che è prroprio questo il bello della mia soluzione!
Trovo infatti le lunghezze dei lati del triangolino ignorando dove stanno i vertici (i quali vanno a posizionarsi "spontaneamente" dove la tensione dell'elasstico viene ad essere la minima possibile
Ma ho altro da ridire a riguardo di questa tua critica (pardon; tuo giusto rilievio] ... e lo metto dentro a "spoiler".
Testo nascosto, fai click qui per vederlo
Il fatto è che la versione del quiz passato in "Rudi Mathematici" chiedeva proprio soltanto quanto valesse il perimetro del triangolo a perimetro minimo inscritto in un trìangolo di lati lunghi rispettivamente 17, 25, 26. Naturalmente il quiz meritava una generalizzazione, soprattutto per il fatto che l'idea dell'elastico m'è venuta per prima, per cui la risposta numerica l'ho calcolata come applicazione della suluzione generalizzata (per un triangolo acutangolo di lati di lunghezza [simbolica] a, b e c)
Però ... nel testo che ho messo in spoiler c'è spiegato un po' tyutto, e cioè:
• che i tre triangolini con un vertice in comune col triangolone ABC ono tutti simili a questo;
• che i due angoli di inclinazione di due lati dell'elastico sul lato di ABC nel quale hanno un estremo comune sono uguali all'angolo opposo a quel lato di ABC;
• che in ciascuno dei tre triangolini simili al triangolone il lato costituito dall'elastico è ricavabile dal lato che in ABC è opposto all'angolo in comune moltiplicandolo per il coseno di quell'angolo
• e (in fine) che dalla similitudine di tre triangoli col triangolone si ricavano facilmente TUTTE le lunghezze dei 9 segmenti.
Per esempio, considerando (nella mia figura che ripeto):

che le inclinazione di FE e di FD su AB valgono γ (cioè quanto l'angolo opposto ad AB, quello in C), iccome – come ho detto –
$u = a·cos(α)$ e $v= b·cos(β)$,
viene per forza
FA=$b·cos(α)$ e BF[/Ii= $a·cos(β)$.
Guarda caso, questi valori sono proprio le proiezioni ortogonali dei latt di lunghezza [i]b ed a su quello di lunghezza c,
In altre parole F è il piede delll'altezza di ABC relativa ad AB su AB stesso.
[Analogamente si dica per D ed E].
Insomma: dove stanno i vdertici di DEF non l'ho detto perché pensavo che non fosse richiesto. Ma da quanto si trova col metodo dell'elastico risulta subito (proprio in base a quanto ho detto esplicitamente).
Da notare che, come è indicato nella figura (in cui, come al solito, i simboli x, y e z rappresentano incognite), prima di calcolare le lunghezze u, v e w, bisogna venir a conoscere
x = AF, y = BD e z = CE
che dànno i rapporti di proporzione rispettivamente di AEF, DBF e DEC con ABC.
Insomma: dove stanno i vertici D, E e F non è detto esplicitamente; ma tra le righe è detto quanto valgono i 6 segmenti individuati suui lati di ABC dai vertici di DEF.
Però ... nel testo che ho messo in spoiler c'è spiegato un po' tyutto, e cioè:
• che i tre triangolini con un vertice in comune col triangolone ABC ono tutti simili a questo;
• che i due angoli di inclinazione di due lati dell'elastico sul lato di ABC nel quale hanno un estremo comune sono uguali all'angolo opposo a quel lato di ABC;
• che in ciascuno dei tre triangolini simili al triangolone il lato costituito dall'elastico è ricavabile dal lato che in ABC è opposto all'angolo in comune moltiplicandolo per il coseno di quell'angolo
• e (in fine) che dalla similitudine di tre triangoli col triangolone si ricavano facilmente TUTTE le lunghezze dei 9 segmenti.
Per esempio, considerando (nella mia figura che ripeto):

che le inclinazione di FE e di FD su AB valgono γ (cioè quanto l'angolo opposto ad AB, quello in C), iccome – come ho detto –
$u = a·cos(α)$ e $v= b·cos(β)$,
viene per forza
FA=$b·cos(α)$ e BF[/Ii= $a·cos(β)$.
Guarda caso, questi valori sono proprio le proiezioni ortogonali dei latt di lunghezza [i]b ed a su quello di lunghezza c,
In altre parole F è il piede delll'altezza di ABC relativa ad AB su AB stesso.
[Analogamente si dica per D ed E].
Insomma: dove stanno i vdertici di DEF non l'ho detto perché pensavo che non fosse richiesto. Ma da quanto si trova col metodo dell'elastico risulta subito (proprio in base a quanto ho detto esplicitamente).
Da notare che, come è indicato nella figura (in cui, come al solito, i simboli x, y e z rappresentano incognite), prima di calcolare le lunghezze u, v e w, bisogna venir a conoscere
x = AF, y = BD e z = CE
che dànno i rapporti di proporzione rispettivamente di AEF, DBF e DEC con ABC.
Insomma: dove stanno i vertici D, E e F non è detto esplicitamente; ma tra le righe è detto quanto valgono i 6 segmenti individuati suui lati di ABC dai vertici di DEF.
________


Ultima modifica di Erasmus_First il 10/11/2019, 16:15, modificato 1 volta in totale.
-

Erasmus_First - Senior Member

- Messaggio: 880 di 1805
- Iscritto il: 11/12/2014, 11:41
Re: Triangolo nel triangolo
@Erasmus
Avrai anche corretto "i dollari" ma io continuo a vedere "sballata" la parte finale del tuo post (precedente).
Boh!
Vedi che ho ragione io?
Cordialmente, Alex
Avrai anche corretto "i dollari" ma io continuo a vedere "sballata" la parte finale del tuo post (precedente).
Boh!
Erasmus_First ha scritto:… ma è vero che non dico quall è il triangolo inscritto con tale perimetro, ...
Vedi che ho ragione io?

Testo nascosto, fai click qui per vederlo
Oh, non discuto la tua bella soluzione (inciso: anche la seconda soluzione che ho postato parte da una premessa simile e "fisica" anch'essa ovvero la "riflessione ottica") ed è vero che ho chiesto la dimostrazione ma la prima richiesta (esplicita) riguardava quale triangolo ha quella caratteristica, al fine di stabilire un teorema generale: Il triangolo dal minor perimetro inscritto in un triangolo acutangolo è quello formato unendo i piedi delle tre altezze (altro inciso: nel testo originale dice "pedal triangle" così ho imparato una nuova parola che non conoscevo  )
)
A titolo di curiosità aggiungo che la seconda soluzione che ho postato è dovuta a H.A.Schwarz (quello della disuguaglianza) mentre la prima ad un suo allievo, L.Fejér
A titolo di curiosità aggiungo che la seconda soluzione che ho postato è dovuta a H.A.Schwarz (quello della disuguaglianza) mentre la prima ad un suo allievo, L.Fejér
Cordialmente, Alex
- axpgn
- Cannot live without

- Messaggio: 14423 di 40677
- Iscritto il: 20/11/2013, 22:03
19 messaggi
• Vai alla pagina... • 1, 2
Chi c’è in linea
Visitano il forum: Nessuno e 1 ospite