Un’ automobile parte da ferma con accelerazione costante uguale a 2,00m/s^2. Calcola lo spazio percorso dall’ auto quando ha raggiunto la velocità di 32,0m/s.

SVOLGIMENTO:

$t=v/a= 32,0m/s / 2,0 m/s^2= 16s$

$s= 1/2*a*t^2= 1/2* 2,00m/s^2* (16^2)s^2= 256m$

Due automobili viaggiano di moto uniforme lungodue strade rettilinee formanti tra loro un angolo retto. Calcola a quale distanza in linea d’ aria si trovano dopo 10 minuti, supponendo che le automobili siano partite nello stesso istante dall’ incrocio delle due strade con velocità una di 90,0 Km/h e l’ altra di 144Km/h.

SVOLGIMENTO:

$s_1= v_1*t= 25m/s* 600s= 15000m=15 Km$

$s_2= v_2*t= 40m/s* 600s= 24000m= 24Km$

$s= (s_1^2+s_2^2)^(1/2)= (15^2+24^2)^(1/2)Km= 28,3 Km$

Due auto da corsa si muovono lungo una pista rettilinea. A un certo istante una delle due auto precede l’ altra di 30,0m ; l auto A che è in vantaggio, viaggia a una velocità di 120 Km/h, mentre l’ auto B cerca di guadagnare terreno avanzando a 125 Km/h. Nell’ ipotesi che i due veicoli mantengano inalterate le loro velocità, dopo quanto tempo l’ auto B raggiunge l’ auto A???

	spazio	tempo	velocità
AUTO A	x+30m	?	120 Km/h
AUTO B	x m	?	125 Km/h

SVOLGIMENTO:

$s_A+(v_A*t)= s_B+(v_B*t)$

$x+30+33,3t=x+34,7t$

$1,4t= 30$

$t=21,4s$

Due fratelli, Stefano e giuseppe, frequentano la stessa palestra. Un pomeriggio Stefano decide di andare in palestra senza aspettare il fratello, che deve terminare di fare i compiti. Sono le 17.00 quando Stefano esce di casa e si dirige verso la palestra, tenendo una velocità di 1m/s. Dopo 10 minuti anche Giuseppe esce di casa per recarsi in palestra. Raggiunge quest ultimo proprio mentre sta davanti allla porta della palestra, alle 17.20. Assumendo che il moto di entrambi i fratelli sia rettilineo uniforme, stabilisci con quale velocità si è mosso Giuseppe e quanto dista la palestra dall’ abitazione dei due ragazzi.

	PARTENZA	ARRIVO
Stefano	17.00	17.20
Giuseppe	17.10	17.20

SVOLGIMENTO:

Ricaviamo da stefano lo spazio che separa la casa dei frateli dalla loro palestra:

$s= v*t= 1m/s* 1200s= 1200m= 1,2Km$

Da ciò la velocità di Giuseppe:

$v=s/t= 1200m/ 600s= 2m/s$

Quale deve essere la pressione in una conduttura dell’ acqua se un pompiere deve fare arrivare il getto a 12m?

SVOLGIMENTO:

$P= d*g*h+ a= (1,00* 10^3 Kg/m^3 *9,81N/Kg*12m)+1 atm= 2,2atm$

Gli studi dentistici sono dotati di poltrone sollevabili il cui meccanismo è essenzialmente costituito da un torchio idraulico formato da due cilindri muniti di pisytone di sezione diversa. Supponi che una poltrona di questo tipo, con seduto sopra un paziente, pesi complessivamente 2100N. Se il dentista deve applicare con il piede una forza di 55N sul pistone più piccolo affinchè la poltrona inizi a sollevarsi, quanto vale il rapporto fra il raggio del pistone più grande e quello del più piccolo?

SVOLGIMENTO:

$P_1=P_2$

$(2100N/ 3,14*r_1^2)= (55N/3,14* r_2^2)$

$r_1/r_2= (2100/55)^(1/2)= 6,2$

Dopo un intervento chirurgico un paziente viene alimentato per via endovenosa con un liquido a base di glucosio di densità pari a 1,03g/cm^3. Determina qual è la pressione in torr del liquido nel punto di iniezione, sapendo che il contenitore (al cui interno la pressione è di 1 atm) si trova a 61,0cm di altezza rispetto al braccio del paziente

SVOLGIMENTO:

$P= d*g*h= 1,03*10^3Kg/m^3* 9,81N/Kg* 0,61m= 6164Pa= 46,4mmHg$

L’ impianto idraulico di un casale di campagna è alimentato da una cisterna. Se la differenzadi pressione dell’ acqua fra il rubinetto di un lavandino all’ interno del casale e la superficie libera dell’ acqua nella cisterna è di 3,0* 10^5 Pa, a quale altezza h si trova la superficie libera dell’ acqua rispetto al rubinetto?

SVOLGIMENTO:

$h= P/(d*g)= 3,0*10^5 Pa/(1,00*10^3 Kg/m^3* 9,81N/Kg)= 31m$

Se si immerge in un liquido un bullone di volume 27 cm^3, questo subisce una spinta di 0,21N. Qual è la densità del liquido?

SVOLGIMENTO:

$d= S/(V*g)= 0,21N/( 27*10^-6m^3* 9,81N/Kg)= 793Kg/m^3$

Calcola quanto è intensa la spinta di Archimede che un pesce di volume pari a 10,0 dm^3 subisce in mae (densità acqua marina: 1,03g/cm^3)

SVOLGIMENTO:

$S= d*V*g= 101N$

Se il tappetino del mouse di un computer è largo 20 cm e lungo 23 cm, con quanta forza la pressione atmosferica preme su di esso?

SVOLGIMENTO:

calcoliamo anzitutto l’ area del tappetino in m^2:

$A= l_1*l_2= 460cm^2=0,046m^2$

da ciò la forza della pressione atmosferica sarà:

$F= p*A= 1,01*10^5 Pa* 0,046m^2= 4,6*10^3N$

Durante un contrasto in una partita di calcetto due avversari calciano il pallone contemporaneamente. Sapeno che ciascuno dei due calciatori esercita sul pallone una forza di 20N, calcola la forza risultante nei casi in cui l’ angolo formato dalle due rorze sia di 90°, 120° e 180°.

SVOLGIMENTO:

CASO 1

$R= (F_1^2+F_2^")^(1/2)= 28,3N$

CASO 2

qui le due forze vanno a creare un triangolo isoscele con angoli alla base di 30° da cui:

R_x= 10N e  R_y= 10* 3^(1/2)N.

quindi:

$R= (R_x^2+R_y^2)^(1/2)= 20N$

CASO 3

$R= F_1+ F_2= 20N-20N= 0N$

Un lungo palo di legno èmantenuto in posizione verticale da un cavo avente un’ estremità fissata a terra a 7,00m dalla base del palo, e l’ altra estremità inserita in un gancio conficcato nel palo, a una quota di 10m da terra. quanto è lungo il cavo? se la forza esercitata dal cavo sul palo ha modulo 500N, quali sono i moduli dei suoi componenti orizzontale e verticale?

SVOLGIMENTO:

la lunghezza del cavo sarà:

$L=(s^2+h^2)^(1/2)= (10,0^2+7,0^2)^(1/2)= 12,2m$

$cos A= 7/12,2$ => $A= 55°$

Da ciò le componenti saranno:

$F_x= F*cos A= 500N* cos 55= 287N$

$F_y= F*sen A= 500N* sen 55°= 410N$

Dati due vettori a e b di cui il vettore a di intensità pari a 3u è sull’ asse y e il vettore b di intensità pari a 4u è sull’ asse delle x, calcola il modulo di c tale che la somma dei tre vettori sia nulla.

$c= (a^2+b^2)^(1/2)= (3^2+4^2)^(1/2)= 5u$

Se una valigetta di massa 2,7 Kg viene appesa a un dinamometro disposto verticalmente, qual è l’ intensità della forza peso misurata dallo strumento?

SVOLGIMENTO:

Anzitutto osserviamo la situazione:

    da ciò deduciamo che sia la gravità ad agire su questo corpo:

$P= m*g= 2,7Kg* 9,81m/s^2= 26N$

Di quanto si allunga una molla di costante elastica 18N/m, se soggetta all’ azione di una forza di intensità 8,8N?

SVOLGIMENTO:

La soluzione risulta banalmente ottenibile mediante una semplice formula:

$X= F/K= 8,8N/ 18N/m= 49cm$

Un uomo e suo figlio devono sollevare una tanica d’ acqua da terra. Il bambino esercita una forza di 70N e l’ uomo una forza di 240N. Sapendo che le due forze sono ortogonali fra loro e che equilibrano il peso della tanica, determina il valore di quest’ ultimo.

SVOLGIMENTO:

il peso della tanica è ricavabile col teorema di Pitagora:

$P= (F_1^2+F_2^2)^(1/2)= (70^2+240^2)^(1/2)N=250N$

Alle due estremità di una riga lunga 100cm e di peso trascurabile sono applicate due forze parallele e di verso concorde di intensità pari rispettivamente a 1N e 4N. Per mantenere in equilibrio la riga si applica a essa un’ altra forza parallela alle due. Qual è l’ intensità di questa forza? Il suo verso è uguale od opposto a quello delle altre due forze?

SVOLGIMENTO:

per essere in equilibrio la somma dei momenti delle forze deve essere uguale a zero:

$(F_1+F_2)*b=F*b$

$F=F_1+F_2= 4N+1N=5N$

Un autista applica al volante del suo veicolo le due forze rappresentate in figura. Ricava il raggio del volante sapendo che il momento della coppia di forze è 25Nm.

SVOLGIMENTO:

A questo punto applichiavo la formula per trovare il braccio della forza in questo caso il diametro dello sterzo:

$b=M/F= 25Nm/ 50N= 0,5m=50cm$

a questo punto troviamo il raggio ricercato:

$r=b/2= 50cm/2= 25cm$

Se spingi uno zaino di 49,0N sul piano di un tavolo devi applicare a esso una forza orizzontale di intensità pari a 6,25N perchè cominci a muoversi, mentre è sufficiente una forza orizzontale di 4,06N perchè lo zaino continui a muoversi a velocità costante. Calcola i coefficienti d’ attrito statico e dinamico fra zaino e tavolo.

SVOLGIMENTO:

$K_1= F_1/P= 6,25N/49,0N= 0,128$

$K_2=F_2/P= 4,06N/49,0N= 0,0829$

Un disco d’ acciaio può ruotare senza attrito attorno a un asse che passa per il suo centro. Il disco ha un diametro di 62,8 cm e a esso vengono applicate due forze di intensità 125N e 90,0N, orientate come mostrato in figura. Qual è il momento risultante delle due forze? Il disco ruota in senso orario o antiorario?

SVOLGIMENTO:

Anzitutto cerchiamo la forza risultante agente sul disco:

$R=F_1-F_2= 125N-90N= 35,0N$

Da ciò il momento sarà:

$M= R* (d/2)= 35,0N* 0,314m= 11,0Nm$

Data una forza F di modulo 4,00N, applicata in un punto P a distanza 6,00m da O, come in figura, quanto vale il momento di F rispetto ad O?

SVOLGIMENTO:

Anzitutto bisogna trovare il modulo della forza che agisce perpendicolarmente al braccio della forza stessa:

$F_P= F* sen A= 4,00N* sen 60° = 3,46N$

da ciò ricaviamo il momento della forza:

$M= F*b= 3,46N* 6,00m= 20,8Nm$

All’ estremità libera di un cavo, fissato a una parete verticale, è appesa una gabbia. La gabbia e il pappagallo pesano 100N complessivamente. Il cavo è appoggiato all’ estremità di una sbarra incastrata nella stessa parete. Determina le intensità della tensione del cavo e della forza vincolare della sbarra.

SVOLGIMENTO:

La tensione del filo è calcolabile:

$T= P/ (sen 30°)= 100N/ 0,5= 200N$

La forza vincolare della sbarra, per contro, è misurabile mediante il teorema di Pitagora. Infatti:

$F= (T^2-P^2)^(1/2)= (200^2-100^2)^(1/2)N= 173N$

Un pompiere di peso P= 830N si trova su una scala di peso trascurabile, appoggiata a un muro liscio. Supponi che la scala sia in equilibrio e, utilizzando i dati forniti in figura, determina l’ intensità della reazione normale del muro. Calcola inoltre le intensità della reazione normale e della forza di attrito statico del pavimento e della scala.

SVOLGIMENTO:

L’ intensità della reazione normale del muro è calcolabile così:

$N_1= P*( d/h)= 830* (2,2/3,8)N=481N$

La reazione normale del pavimento invece:

$N_2= P= 830N$

La forza di attrito statico è invece uguale a N_1:

$F=N_1= 481N$

Tre ragazzi giocano al tiro alla fune con tre funi incernierate in un unico nodo. Se tutti e tre tirano con una forza di uguale intensità, come devono essere orientate le tre funi perchè i ragazzi facciano pari e patta?

Per avere pari e patta gli angoli di incidenza delle forze devono essere uguali:

$A= G/3= 360°73=120°$

Per tenere in equilibrio una scatola di cioccolatini su un piano inclinato liscio lungo 50,0cm e alto 22,5cm occorre una forza di 3,97N. Ricava il peso della scatola.

SVOLGIMENTO:

Il peso lo otteniamo nel seguente modo:

$P= F_p/ senA= F_p/ (h/l)= 3,97N/ (22,5cm/50,0cm)= 8,82N

A un punto materiale sono applicate due forze perpendicolari fra loro, di intensità pari rispettivamente a 6N e 8N. Qual è l’ intensità della forza equilibrante?

SVOLGIMENTO:

La forza equilibrante è data da:

$E=(F_1^2+F_2^2)^(1/2)= (8^2+6^2)^(1/2)N=10N$

Affinchè un pacco appoggiato su un tavolo orizzontale cominci a muoversi, è necessario tirarlo orizzontalmente con una forza di 2N. Quanto vale il coefficiente di attrito statico se il peso del pacco è 20N?

SVOLGIMENTO:

Il coefficiente di attrito lo troviamo con la semplice formula:

$K=F/P= 2N/20N= 0,1$

Sul tavolo di un ristorante è appoggiato un piatto del peso di 2,9N. Qual è l’ intensità della reazione normale sviluppata dalla superficie del tavolo, se un cameriere pone nel piatto una bistecca che pesa 1,5N?

SVOLGIMENTO:

ovviamente la reazione normale del tavolo è uguale alla somma dei pesi degli oggetti disposti sul tavolo:

$N=P_1+P_2= (2,9+1,5)N= 4,4N$

Un cesto di fiori del peso di 50N è fissato con una fune  a una trave di legno. Qual è l’ intensità della forza di tensione della fune????

SVOLGIMENTO:

Ovviamente la tensione della corda sarà uguale al peso del cesto:

$T=P= 50N$

La figura mostra una cassa, di peso uguale a 500N, appesa a una corda verticale che, nel punto P, si conginge con altre due corde fissate a un sostegno. Queste formano con l’ orizzontale angoli di 30° e 60°. Determina quali sono le tensioni di ciascuna delle due corde oblique.

SVOLGIMENTO:

troviamo le due tensioni:

$T_1= P*sen 30°= 500N* 0,5= 250N$

$T_2= P* sen 60°= 500N * sen 60°= 433N$

In un negozio di frutta e verdura una cassa di mele è appoggiata su un piano inclinato alto 50cm e lungo 1,0m. La cassa, che pesa 46N, è tenuta in equilibrio dalla forza di attrito statico.

Qual è l’ intensità della forza di attrito che agisce sulla cassa? qual è l’ intensità della reazione normale del piano? Quanto vale il coefficiente di attrito statico?

SVOLGIMENTO:

La forza di attrito deve essere uguale alla componente parallela del peso:

$F= P* sen A= P*(h/l)= 46N* (0,5m/1,0m)= 23N$

Da ciò sappiamo che il seno dell’ angolo è 0,5 e che quindi l’ angolo è di 30°.

La reazione normale del piano sarà invece uguale alla componente perpendicolare del peso:

$N= P* cosA= 46N* cos30°= 40N$

 Il coefficiente di attrito statico, per contro, lo ricaviamo dalla seguente formula:

$K= F/P= 23N/ 40N= 0,58$

Per svitare un bullone un uomo esercita su una chiave inglese una forza F, orientata come mostrato in figura.Sapendo che il momento di questa forza rispetto al centro del bullone è pari a 29 N m, determina l’ intensità di F.

SVOLGIMENTO:

Calcoliamo anzitutto la forza F_x:

$F_x= M/b= 29N m/ 0,28m= 103,6N$

Da ciò otteniamo F:

$F= F_x/sen 60°= 120N$

Quanto pesa un disco da hockey che, scivolando su una superficie orizzontale di una pista di ghiaccio, è soggetto a una forza di attrito dinamico di 0,32N ? Assumi che il coefficiente di attrito dinamico fra disco e ghiaccio sia K= 0,11

SVOLGIMENTO:

La legge sull’ attrito ci dice che:

$P= F_a/K =0,32N/0,11= 2,9N

Un’ asta omogenea di peso 4N, appesaq per le estremità a due dinamometri D1 e D2, come nella figura, è in equilibrio. Determina le intensità delle forze F1 e F2 misurate dai dinamometri alle due estremità dell’ asta.

SVOLGIMENTO:

Essendo il peso ugualmente distribuito su ambedue i dinamometri secondo l’ immagine fornitaci, la forza su ogni dinamometro sarà uguale alla metà del peso della sbarra:

$F=P/2= 4N/2= 2N$

Scomponi una forza di 50N in due componenti ortogonali fra loro, di cui uno con modulo di 30N. Qual è il modulo del secondo componente?

SVOLGIMENTO:

 La seconda componente va ovviamente trovata col teorema di Pitagora:

$C2=(R^2-C1^2)^(1/2)= (50^2-30^2)^(1/2)N= (2500-900)^(1/2)N= 1600^(1/2)N= 40N$

Rappresentiamo una forza F di intensità 1,0N e scomponiamola in due componenti, inclinati rispetto a F,da parti opposte, rispettivamente di 30° e 60°. Quali sono le intensità delle due forze componenti?

SVOLGIMENTO:

Quindi la prima componente avrà intensità:

$C1= F* cos 60^o= 1,0N * cos 60^o= 0,50N $

La seconda componente invece:

$C2= F* cos 30^o= 1,0N * cos 30^o= 0,87N $

All’ inizio di una coreografia un ballerino solleva la sua compagna da terra. La componente verticale della forza esercitata dall’ uomo è di 130N, mentre la componente orizzontale è di 150N. Calcola il modulo della forza risultante.

SVOLGIMENTO:

Ovviamente la forza risultante sarà l’ ipotenussa di questo triangolo rettangolo:

$F= (F1^2+F2^2)^(1/2)=$ (1502+130^2)^(1/2) N = (22500+16900)^(1/2) N= (39400)^(1/2) N= 198N

Due forze, entrambe di modulo 5,0 N, sono applicate allo stesso punto O. Calcola l’ intensità della loro risultante nel caso in cui le due forze siano collineari e concordi e nel caso in cui siano ortogonali.

SVOLGIMENTO:

1° CASO: COLLINEARI CONCORDI

In questo caso la forza risultante in modulo è uguale alla sommatoria dei moduli delle singole forze:

$F= F1+F2=$ (5,0+5,0) N = 10N

2° CASO: FORZE ORTOGONALI

 

 In questo caso invece il modulo della forza risultante lo potremo ottenere col teorema di Pitagora:

$F=(F1^2+F2^2)^(1/2)=$ 7,1 N

Durante la fase di decollo un aeroplano si stacca dal suolo con una velocità di 600 Km/h , stando inclinato di 15° rispetto alla pista orizzontale. Con quale velocità l’ aereo si innalza verticalmente?

SVOLGIMENTO:

Ovviamente la componente verticale della velocità è quella evidenziata di rosso in figura d cui:

$v_y= v*sen 15^o= 600Km/h* sen 15^o= 155 Km/h$

Durante una partita a dama la pedina nera conquista tre pedine avversarie con tre salti successivi, come mostrato in figura.  Sapendo che ogni casella della scacchiera ha un lato di 4,0cm , calcola lo spostamento effettuato dalla pedina nera per andare dal punto A, nel centro della casella di partenza, fino al punto B nel centro della casella d’ arrivo.

SVOLGIMENTO:

Ovviamente ciò che va preso in considerazione sono le diagonali delle caselle. Le diagonali di un quadrato si trovano:

$d=l*[2^(1/2)]=$ 4*2^(1/2)

Il primo spostamento è lungo quattro caselle quindi:

$S1=4*d=$ 16*2^(1/2) cm

Il secondo spostamento, per contro, avviene secondo due caselle quindi:

$S2= 2*d=$ 8*2^(1/2) cm

Essendo questo un triangolo rettangolo, lo spostamento totale sarà dato dall’ ipotenusa di questo triangolo calcolabile mediante il teorema di Pitagora:

S= [S1^2+S2^2]^(1/2)=$ 25cm

Calcola le componenti cartesiane a_x e a_y di un vettore a di modulo 4 passi, che forma un angolo di 120° con la direzione positiva dell’ asse x di un sistema cartesiano Oxy.

SVOLGIMENTO:

Risulta utile visualizzare graficamente la situazione:

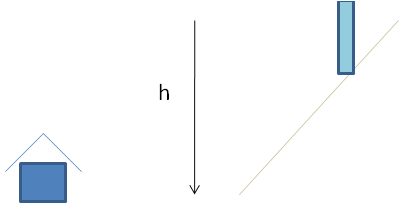
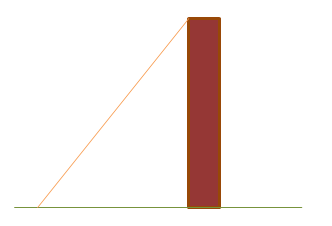
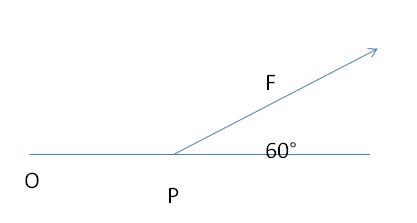
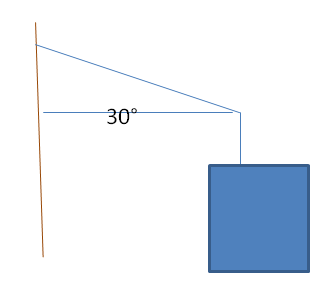
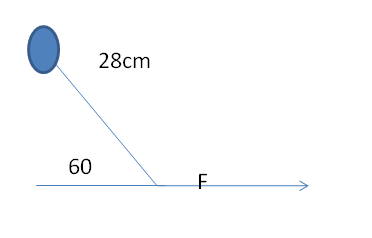
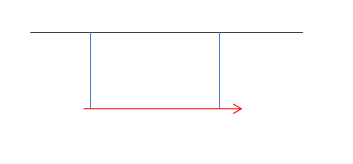
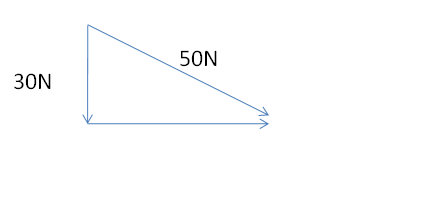
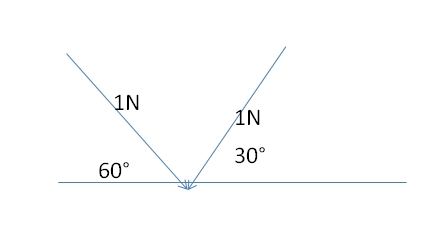
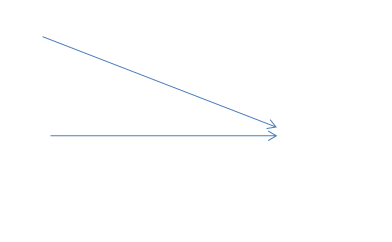
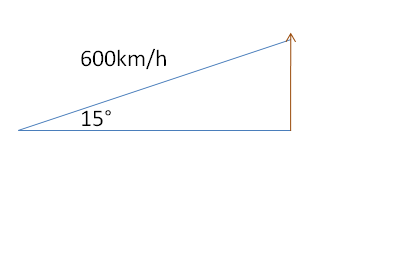
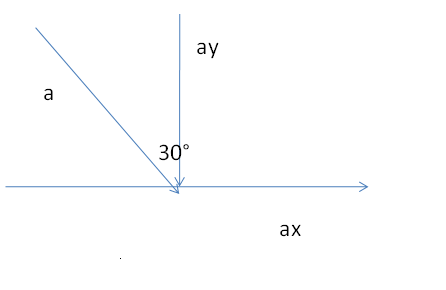Dall’ immagine notiamo la formazione di due triangoli rettangoli sempre risolubili mediante la goniometria:

$a_x= a* cos (180-120)°$ =4 passi* cos 60= -2 passi giacchè a_x si trova sull’ asse negativo delle ascisse

$a_y= a* cos (120-90)°$ = a* cos 30° = 4 passi *cos 30°= 2*[(3)^(1/2)] passi

Fissato un sistema di riferimento cartesiano Oxy e assegnato il vettore a avente componenti cartesiane a_x= 2 passi e a_y= 2 passi, determina il suo modulo e l’ ampiezza dell’ angolo che esso forma con la direzione positiva dell’ asse x.

SVOLGIMENTO:

Ovviamente le cordinate del vettore a formeranno un triangolo rettangolo di cui a_x e a_y sono cateti e a stesso ipotenusa. Dunque:

$a=[(a_x)^2+(a_y)^2]^(1/2)= [(2^2)+(2^2)]^(1/2) = 2* [(2)^(1/2)]$ passi.

questa rappresenta la diagonale del quadrato formato da a_x e a_y  e pertanto l’ angolo sarà di 45°.

Per i più sospettosi:

$a_x= a* cosA$  da cui  $cos A= a_x/ a = [2^(1/2)]/2$  da cui A=45°

Un aeroplano si sposta di 600 km in direzione Sud 30° Ovest. Rappresenta graficamente la situazione. Calcola il modulo dei componenti dello spostamento verso Sud e verso Ovest.

Per semplificare ulteriormente lo svolgimento dell’ esercizio iniziamo dalla visualizzazione grafica dello spostamento:

Da ciò, per le regole della trigonometria:

OVEST= 600Km * cos 30°= 520Km

SUD= 600Km * cos 60°= 300Km

Se, fissata una scala,una velocità di modulo 20km/h viene rappresentata da un segmento orientato lungo 5,0cm, quanto deve essere lungo il segmento orientato che rappresenta una velocità di 30 km/h?

Ovviamente il problema si risolve con una banale proporzione:

20km/h : 5,0cm= 30km/h : xcm

da ciò otterremo la misura del segmento:

X=[(5,0*30)/20]cm= 7,5cm

Una formica cammina sul pavimento di una stanza rettangolare avente un lato l di 12m. La formica parte da un angolo del pavimento e, vanzando a zigzag, arriva all’ angolo opposto. Se il modulo del vettore spostamento è di 13m, quanto è lungo l’ altro lato della stanza?

SVOLGIMENTO:

il vettore spostamento rappresenta l’ ipotenusa del triangolo rettangolo individuato dai due lati della stanza:

$L=[(v^2)-(l^2)]^(1/2)= (13^2-12^2)^(1/2)=5,0m$

Un motoscafo inizialmente fermo in prossimità di una boa si sposta di 100m verso ovest e successivamente di 100m verso sud. Determina di quanto si è allontanato il motoscafo dalla boa.

SVOLGIMENTO:

l’ allontanamento dalla boa del motoscafo lo possiamo calcolare per mezzo del teorema di Pitagora data la perpendicolarità dei vettori spostamento del motoscafo:

$S=[(s1^2)+(s2^2)]^(1/2)$= [(100^2)+(100^2)]^(1/2)= (2*10000)^(1/2)= (20000)^(1/2)=141m

Uno speleologo scende in fondo a un pozzo verticale profondo 20m. Se fissiamo come asse di riferimento una retta verticale orientata verso l’ altoo, con l’ origine O al livello del suolo, la coordinata del fondo del pozzo è -20m. La risalita avviene in due tappe e nella prima lo speleologo compie , dal fondo del pozzo, uno spostamento di 14m. Al termine di questa tappa, qual è la coordinata della posizione raggiunta? quale lo spostamento dal livello del suolo? e quale la lunghezza totale del percorso compiuto?

SVOLGIMENTO:

S=(-20+14)m= -6m

a questo punto lo speleologo si trova sei metri sotto il livello di terra quindi il suo spostamento rispetto al suolo sarà di 6m.

il percorso totale lo si ottiene sommando la profondità P del pozzo con il cammino C dello speleologo:

$T=P+C$= (20+20-6)m=34m  infatti lo speleologo ha prima sceso tiutti e venti i metri del pozzo per poi risalire di quattordici metri per giungere a quota -6m.

un marinaio e un passeggero si trovano sul ponte di una nave. Mentre la nave si allontana di 30m dal molo da cui è partita,il passseggero percorre 8,0m nel verso di navigazione della nave, invece il marinaio ne percorre 5’0m in senso opposto.

Determina il modulo dello spostamento risultante del passeggero e del marinaiodal molo.

SVOLGIMENTO:

una visualizzazione grafica del problema può sicuramente aiutarci a trovare la soluzione a questo quesito:

PASSEGGERO: la nave si sposta di 30m dal molo e lui percore altri 8,0m nello stesso verso di moto:

 ———–>30m+ —–>8,0m

PASSEGGERO= (30+8.0)m=38m

MARINAIO: dopo il movimento della nave lui percorre 5,0 m con verso opposto a quello della nave:

————> 30m+ <— 5,0m

MARINAIO: essendo il verso del suo spostamento opposto a quello da noi considerato positivo avremo:

M=(30-5,0)m=25m