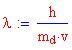
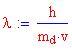
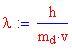
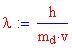
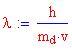
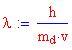
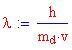
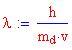
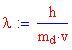
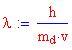
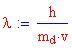
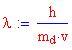
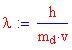
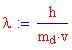
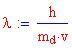
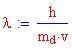
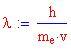
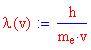

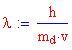
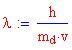
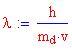
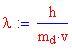
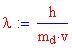
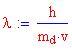
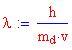
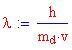
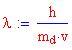
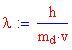
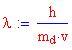
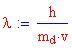
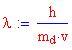
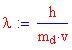
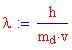
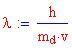
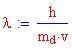
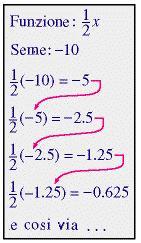
Iterare una funzione significa valutare la funzione ripetutamente. Nella prima iterazione, la funzione è valutata per un valore iniziale (chiamato seme ). Nella seconda iterazione la funzione è valutata per il valore uscito dalla prima iterazione e così via.
La sequenza dei valori in uscita è chiamata orbita della funzione iterata per il seme assegnato.
Una delle cose meravigliose dell'era dei computer è che possiamo demandare agli elaboratori elettronici calcoli noiosi (come quelli delle iterazioni), che essi svolgono in una frazione di secondo.
Ecco una procedura che valuta una funzione iterata per un seme assegnato. Questa procedura usa una variabile intervallo e una variabile indice per mantenere la traccia delle successive iterazioni.
L'orbita è rappresentata qui sotto. Quale effetto produce il seme sull'andamento dell'orbita?
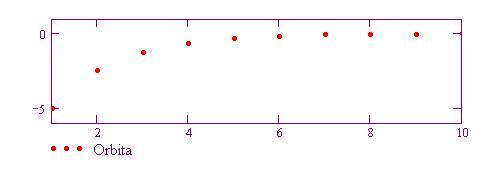
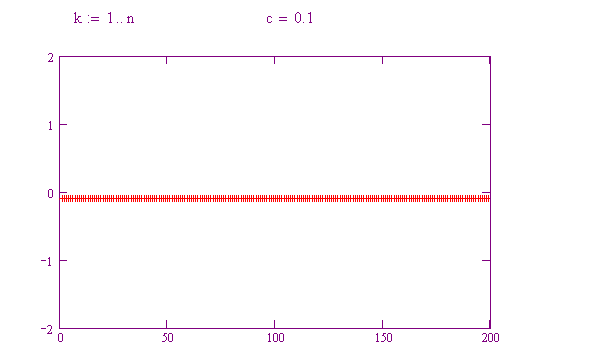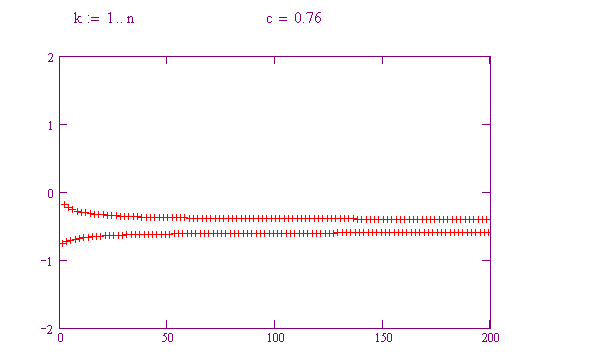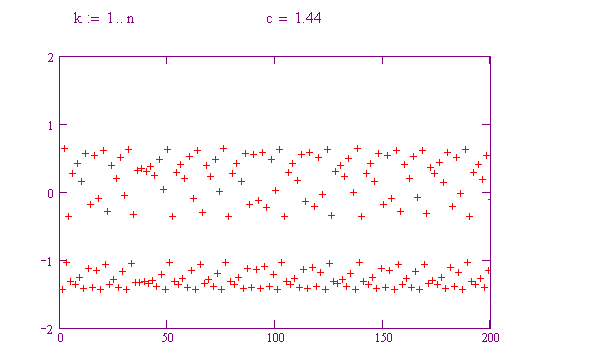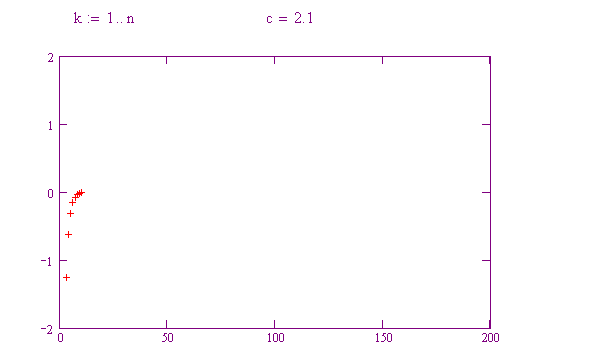
A seconda della funzione da iterare e del valore per il seme scelto, si possono scoprire comportamenti molto diversi per l'orbita.

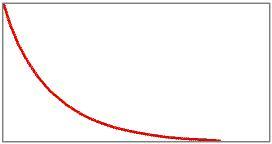

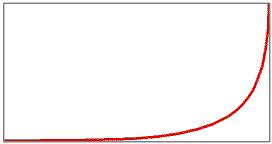
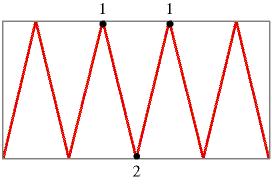
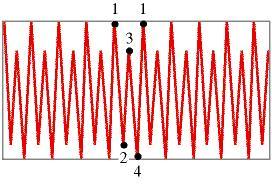
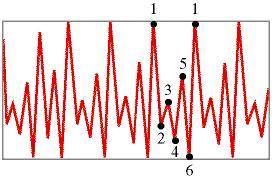
Qui l'orbita oscilla tra due valori ed è detta periodica con periodo 2.
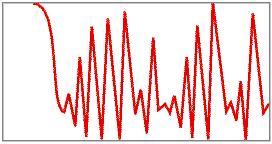
Qui non è riconoscibile alcuna struttura. Questo comportamento è detto caotico!
Anche sistemi dinamici semplici possono presentare un andamento imprevedibile o caotico. Qui sotto itereremo una famiglia di funzioni della forma f(x) = x 2 – c, per vedere come piccole variazioni del valore di c possono dare origine a comportamenti molto diversi.
Iterare la funzione per differenti valori di c (c è globalmente definito sotto), mantenendo costante il valore del seme
.
Provate a far variare c da 0.1 a 0.2, poi 0.3, poi 0.4, poi 0.5, e così via fino a 2. Notate il diverso comportamento delle orbite! Per ogni valore di c, rappresentate il tipo di comportamento mostrato.
lo facciamo noi per voi con il grafico di una funzione parametrica che presenta proprio c come parametro
In questo file illustreremo le vibrazioni libere in sistemi meccanici e in sistemi elettrici rappresentate da equazioni differenziali del secondo ordine lineari omogenee con coefficienti costanti.
Consideriamo un carrello di massa M, collegato ad una molla che esercita una forza, proporzionale alla distanza dal centro di oscillazione, uguale a , con attrito viscoso del mezzo espresso da una forza del tipo
.
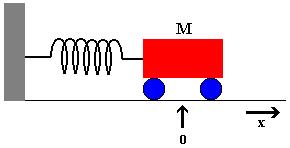
Trasformazione nella forma standard:
La soluzione simbolica esatta viene riportata qui sotto.
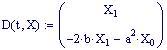
Consideriamo un semplice circuito elettrico contenente una resistenza, una induttanza e un condensatore. La variazione di Q sulle superfici del condensatore è rappresentata dalla seguente equazione differenziale:
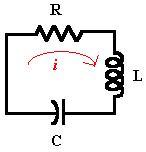
Trasformazione nella forma standard:
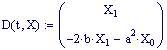
Questi appunti mostrano le varie fasi per la costruzione del il sistema di equazioni che descrivono il moto di un pendolo smorzato a partire dalle:
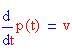
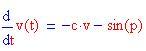
E' possibile costruire soluzioni sull'intervallo temporale [0,20] per una serie di condizioni iniziali , usando una tecnica numerica detta
Dapprima si sceglie un numero di passi e si definiscono variabili di escursione per generare le soluzioni:
Per generare otto soluzioni, conviene calcolarle a blocchi. Bisogna definire un vettore derivativo che dia le derivate di p e v per quattro soluzioni. Si verranno ad aggiungere altre righe alla matrice risolutiva. La costante di smorzamento c viene posta uguale a 0.2 .
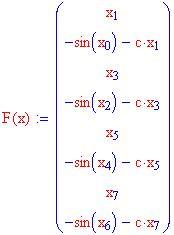
Ora si scelgono otto condizioni iniziali. In questo esempio , alcune traiettorie vengono fatte partire dalla posizione 0 con velocità positiva, e altre dalla posizione 2 p con una velocità negativa:
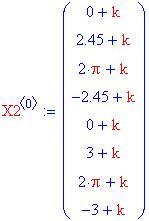
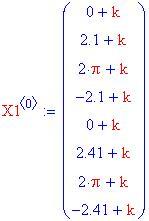
Queste equazioni sviluppano l'approssimazione del passo Runge–Kutta che generera le traiettorie seguenti:
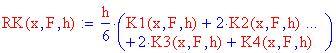
Le due seguenti equazioni definiscono iterazioni sull'indice i per generare le otto traiettorie . Per facilità di manipolazione, le condizioni iniziali vengono riunite in un sola matrice x . La colonna i-sima di x contiene le otto soluzioni , con le posizioni negli elementi pari e le velocità negli elementi dispari.
Nell'interpretazione di un tracciato di fase è utile sapere la direzione e il verso secondo cui evolve ogni soluzione. Da solo, il grafico della soluzione non da questa informazione, ma può essere aggiunta posizionando frecce lungo la traiettoria che indichino la direzione corrispondente al variare del tempo. Le seguenti definizioni (alquanto complicate) hanno lo scopo di creare uno spazio ogni quindicesima colonna di x e di inserire punti che disegneranno le frecce.
La funzione seguente genera un vettore unitario nella direzione della freccia, che è la direzione del vettore che unisce il punto precedente al successivo. La variabile indipendente a questa funzione sarà una schiere due per due dove la prima fila denota le posizioni e la seconda le velocità per una soluzione particolare.
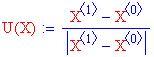
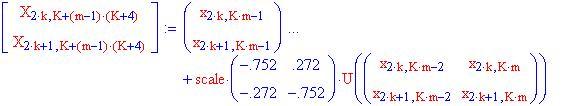
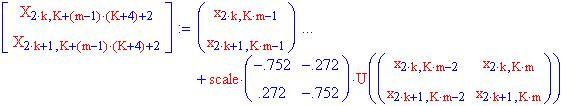
Ecco rappresentato lo spazio delle fasi completo, con la posizione angolare sull'asse orizzontale e la velocità angolare sull'asse verticale.
Tre punti di equilibrio, segnati da rettangoli neri, sono visibili in questo tracciato: due punti di equilibrio stabile in (0, 0) e (2 p , 0) , e un punto di equilibrio instabile in ( p , 0) .
Tutte le traiettorie tratteggiate in rosso hanno (0, 0) come loro limite: esse giacciono nel bacino di attrazione di questo punto di equilibrio. Le traiettorie blu, a linea continua, alla fine girano in spirale verso il prossimo equilibrio in (2 p , 0) . L'equilibrio instabile in ( p , 0) rappresenta uno stato dove il pendolo è senza moto ma la massa pendolare è all' inizio del ciclo. Quattro delle traiettorie si avvicinano molto a questo punto. In due di queste il pendolo raggiunge quasi la cima e poi cambia la direzione e ricade; per le altre due il pendolo ce la fa appena a superare la cima cadendo poi nella regione successiva del dominio angolare. Si può vedere dall'assembramento delle frecce vicino all'equilibrio instabile quale posizione e quale velocità sta cambiando lentamente in questa regione dello spazio delle fasi.
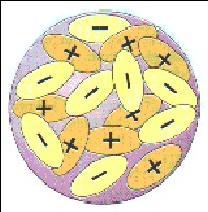
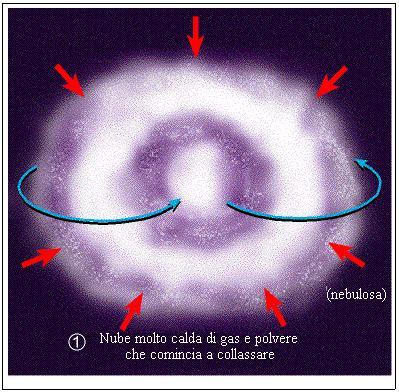
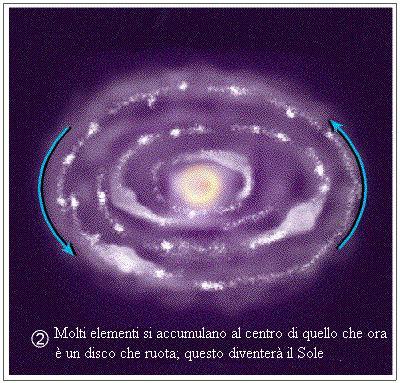
Abbiamo tutti sentito parlare di elementi radioattivi, ma cosa sono? In sostanza, sono elementi il cui il nucleo emette radiazioni in una di queste tre forme:
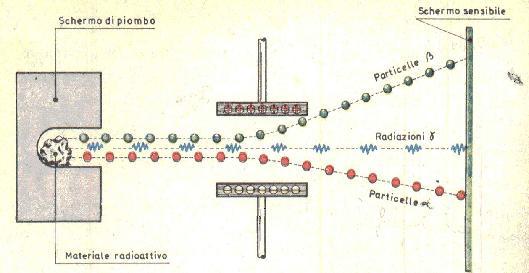
Le sostanze radioattive emettono spontaneamente particelle elettriche positive( a ) negative( b ) e radiazioni elettromagnetiche( g )
radiazioni alfa: il nucleo emette particelle ad alta energia (due protoni e due neutroni) di un atomo di elio (senza gli elettroni)
radiazioni beta: il nucleo emette elettroni ad alta energia, mentre un neutrone si trasforma in un protone
radiazioni gamma: il nucleo emette un fotone ad alta energia.
Gli elementi si presentano in varie forme. Quelli riscontrati nella tabella periodica sono solo i più stabili. Tuttavia, esistono anche forme instabili. Il carbonio, per esempio, con numero di massa 12 (che corrisponde a 6 protoni + 6 neutroni) è presente in una forma con numero di massa 14 ( 6 protoni e 8 neutroni). In questa forma risulta instabile perché ci sono più neutroni che protoni. Così i neutroni in eccesso diventano un protone ed un elettrone. L'elettrone viene espulso, e l'atomo rimane con 7 protoni e 7 neutroni e diventa stabile. Questo processo viene chiamato decadimento beta .
Come avrete indovinato un nucleo sottoposto a decadimento beta espelle due neutroni e due protoni, mentre un nucleo sottoposto a decadimento gamma espelle un fotone ad alta energia (questo è il risultato della ridistribuzione di carica all'interno del nucleo).
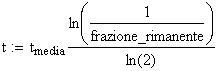
Il tempo richiesto perché metà di un campione radioattivo decada viene detto vita media. Il carbonio 14, per esempio, usato per determinare l'età di materia una volta organica (vivente), ha una vita media di 5730 anni. In tal modo se in origine in un osso ci fosse stato una quantità x di carbonio 14, 5730 anni dopo ce ne sarebbe solo x/2, e dopo altri 5730 anni ne rimarrebbe x/4, e ancora, dopo altri 5730 anni ne rimarrebbe x/8 e così via.
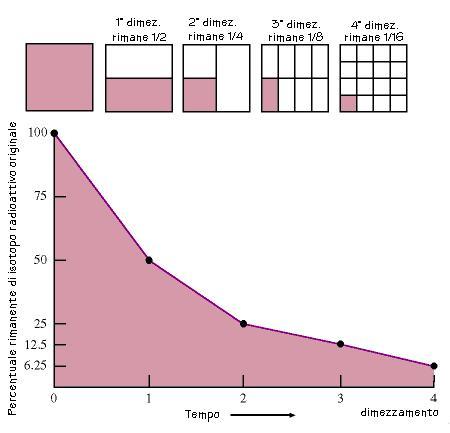
Se si riesce a determinare quante vite medie sono trascorse dal momento della creazione di un campione radioattivo, si riesce a determinare quanto tempo fa quel campione è stato creato.
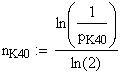
Queste cifre di fatto si riferiscono all'età di una roccia lunare nella quale si riscontrò mancante l' 82% del suo conteggio originale di potassio -40 .
In Italia venne trovato un uomo congelato. La cosa strana è che l'uomo corrisponde alle caratteristiche di un uomo dell'Età della Pietra, che aveva con sé persino attrezzi dell'Età della Pietra.
(L'Età della pietra arriva fino a 5000 anni fa, quando l'uomo imparò a fondere il metallo ed entrò nell'Età del Bronzo).
Il carbonio 14 viene continuamente creato nell'atmosfera e viene assorbito da tutti gli organismi viventi. Mentre sono vivi, gli organismi mantengono un equilibrio tra il decadimento e l'assorbimento di nuovo carbonio-14. Dopo la morte, tuttavia, l'assorbimento cessa, ma il decadimento continua, così la quantità di carbonio -14 diminuisce. Conosciamo il tasso di decadimento del carbonio -14 e sappiamo quanto carbonio -14 c'è in un organismo vivente, così misurando quanto carbonio manca, possiamo determinare quando l'organismo è morto.
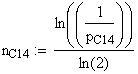
La datazione al carbonio è buona per materiale organico, ma per datare rocce o altri oggetti inorganici?
Il trucco sta nel trovare un isotopo instabile con una vita media molto lunga. Grazie a Madre Natura, il potassio-40, con vita media di 1.25 x 10 9 anni, risulta praticamente perfetto. (Questo metodo di datare materiale si chiama datazione al radioisotopo ).
Per esempio, degli scienziati riscontrarono che una roccia lunare ha 82% del suo potassio-40 iniziale. Quanto è vecchia la roccia?




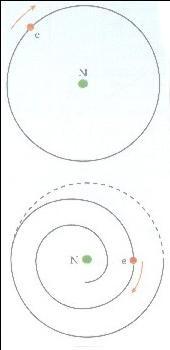 |
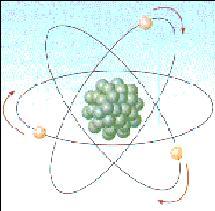
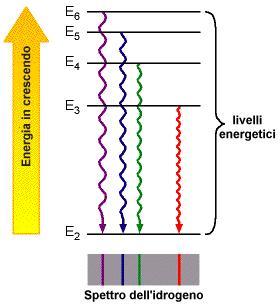
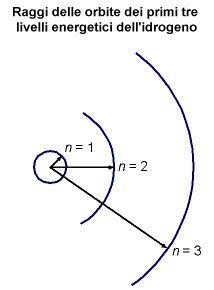
Questa teoria presentava però un problema. Come sapete quando una particella si muove lungo un'orbita circolare subisce un'accelerazione verso il centro del cerchio: l'accelerazione centripeta.
E quando un elettrone viene accelerato, emette radiazioni elettromagnetiche o luce. Per la tesi della conservazione dell'energia, l'energia di questa luce deve provenire dall'energia necessaria a percorrere l'orbita, così l'orbita dell'elettrone dovrebbe restringersi fino a cadere sul nucleo.
|
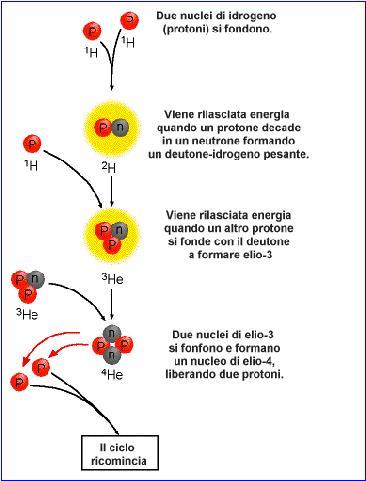
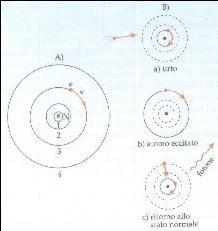 |
Il più basso livello di energia in cui può stare l'elettrone di un atomo si chiama
stato fondamentale ,
e quando assorbe un fotone per muoversi ad un livello maggiore, questo si chiama
stato eccitato.
|
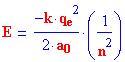
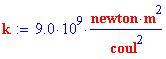
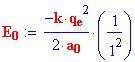
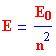
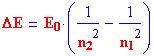
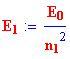
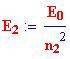
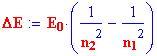
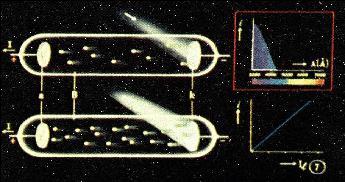
Racchiudendo sotto vuoto il metallo emettitore in un bulbo di vetro, nel quale venga introdotto un anodo collegato al polo positivo di una pila, si realizza una cellula fotoelettrica. E' possibile così raccogliere gli elettroni emessi dal metallo e misurare mediante un milliamperometro l'intensità della corrente.
Nel tardo 800 i risultati di alcuni esperimenti indicavano che, quando la luce ultravioletta colpiva una lastra di zinco carica negativamente, questa si scaricava.
Ciò accadeva solo con luce ultravioletta. Con raggi di luce di frequenza più piccola (lunghezza d'onda più lunga) il fenomeno non si verificava. Altri esperimenti vennero effettuati e si dimostrò che per materiali diversi dallo zingo erano altre frequenze a permettere l'emissione di elettroni. Cosi si cercò di spiegare questo fatto.
Nell'ambito della fisica classica i risultati sperimentali potevano essere spiegati con l'idea che quando le onde luminose colpivano gli elettroni, questi si sarebbero messi a vibrare fino a quando non avessero raggiunta l'energia sufficiente per essere emessi dalla piastra. Tuttavia ci sono dei punti deboli in questa spiegazione.
Nel 1905, lo stesso anno in cui scrisse la teoria della Relatività Speciale , Albert Einstein avanzò una soluzione che rispondeva a tutti questi problemi.
L'energia della luce è quantizzata . In altre parole, piuttosto che essere distribuita lungo il fronte d''onda, l'energia arriva in piccoli pacchetti detti fotoni. E l'energia di questi fotoni è
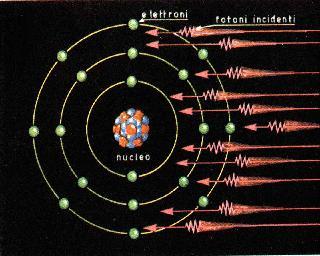
Secondo la teoria di Einstein l'energia raggiante non solo viene emessa e assorbita per quanti, ma si propaga anghe per quanti. In altre parole Einstein ammise che l'energia elettromagnetica si propaga nello spazio concentrata in piccoli granuli e non distribuita sul fronte d'onda come è richiesto dalla teoria ondulatoria. Ognuno di tali granuli, cui egli diede il nome di fotone, ha un'energia data dalla formula di Plank, cioè W =h .f
Questa ipotesi spiega i risultati ottenuti sperimentalmente. Appena un fotone con sufficiente energia colpisce un elettrone, l'elettrone l'assorbe ed acquisisce una energia sufficiente a liberarsi dei suoi legami atomici. La quantità minima di energia necessaria a causare ciò corrisponde direttamente alla frequenza critica menzionata sopra. E quando il fotone ha maggior energia rispetto a quella richiesta, quella energia in più viene convertita in energia cinetica per gli elettroni emessi secondo la formula
Quando descritto precedentemente viene indicato e rappresentato dai termini dualità onda-corpusolo . La luce si comporta ancora come una sorgente continua di onde, ma presenta una quantizzazione di energia che ci costringe a considerarla anche come particella.
L'energia di un fotone con questa frequenza è praticamente pari a
Questi sono i valori della energia, frequenza e lunghezza d'onda di un fotone che ricevete a 94.3 MHz sul vostro sintonizzatore radio FM.
Nel 1923 un fisico americano, Arthur Compton, eseguì un esperimento che convalidava la teoria di Einstein sulla quantizzazione dell'energia nella luce.
Come sapete una carica, come l'elettrone, genera un campo elettrico. Tuttavia, quando si muove, la carica genera sia un campo elettrico che un campo magnetico: una variazione periodica del campo elettromagnetico viene chiamata radiazione elettromagnetica, meglio nota come luce. La luce è semplicemente un campo elettrico oscillante assieme ad un campo magnetico oscillante perpendicolarmente al primo.
Compton sparò raggi x verso una lastra di grafite. Secondo la teoria classica (al contrario della meccanica quantistica), gli elettroni nella lastra avrebbero assorbito le onde luminose ed iniziato ad oscillare con la stessa frequenza della luce. In questo movimento avrebbero incominciato ad emettere radiazione elettromagnetica con la stessa frequenza dei raggi x, cioè , avrebbero cominciato ad emettere raggi x.
Si certo, vennero emessi raggi x, ma un congruo numero di essi aveva una frequenza minore di quelli iniziali! L' equazione di Einstein, applicata a questo caso, ci dice che questi raggi possedevano meno energia. L'interpretazione di questo risultato portò a confermare che i fotoni esistevano davvero e che quando essi si scontravano con gli elettroni della grafite cedevano un pò di energia agli elettroni. Una teoria è buona quanto l'evidenza dei fatti sperimentali la supporta, e questa era un'ottima prova dell'esistenza di fotoni.
Compton riuscì a dimostrare che la variazione di frequenza dei raggi x emessi era
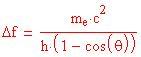
dove m e è la massa di un elettrone e q è l'angolo con cui il fotone veniva diffuso dalla lastra di grafite. Un fotone che rimbalza con un angolo di 90° subisce un cambio di frequenza di
oppure, in termini di lunghezza d'onda
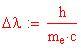
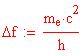
Quest'ultimo valore viene chiamato Lunghezza d'onda di Compton dell'elettrone.
E allora qual'è la variazione di energia di un fotone riflesso a 90°?
E se ricordate la celebre equazione E = mc2 potete concludere che questa è semplicemente l'energia a riposo di un elettrone. Tutto ciò ha profonde implicazioni!

Distanza della stella (in parsec):
parsec
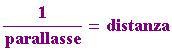



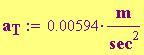

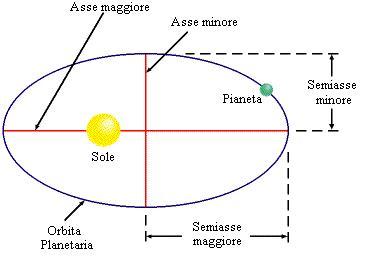
Semiasse maggiore (in AU):
anni
a
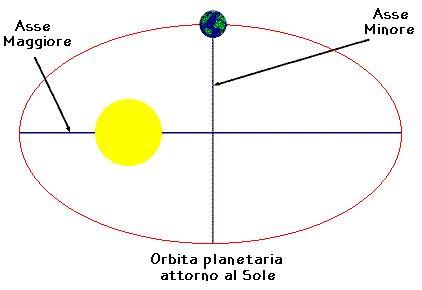
può essere pensato come la distanza media tra un pianeta ed il sole in AU.In questa sezione illustreremo il calcolo per trovare il moto di un satellite, a partire dalla posizione e dalla velocità iniziale, e useremo il metodo di Runge-Kutta del quarto ordine.
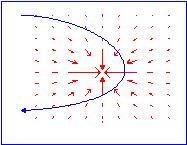
Esamineremo due casi: uno il cui risultato è un'orbita circolare, l'altro , la cui velocità iniziale è minore rispetto alla prima, da come risultato un'orbita ellittica.
La forza dovuta al campo gravitazionale varia in modo inversamente proporzionale al quadrato della distanza dalla sorgente del campo. Pertanto le equazioni differenziali per il moto del pianeta sono:
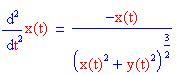
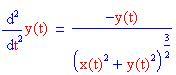
| Originale | Perturbazione | |
| posizione iniziale rispetto a x : | |
|
|
posizione iniziale rispetto a y :
|
|
|
|
velocità iniziale in direzione x :
|
|
|
|
velocità iniziale in direzione y:
|
|
|

La traiettoria è un'ellisse se il pianeta è sottoposto ad un campo gravitazionale centrale diretto
verso il fuoco (prima legge di Kepler). Osserva la seguente animazione
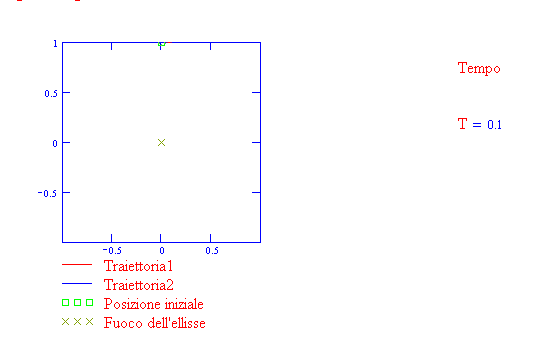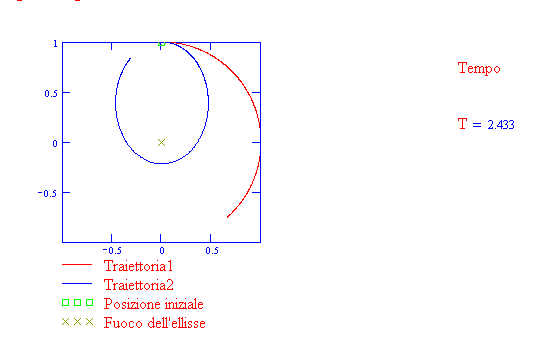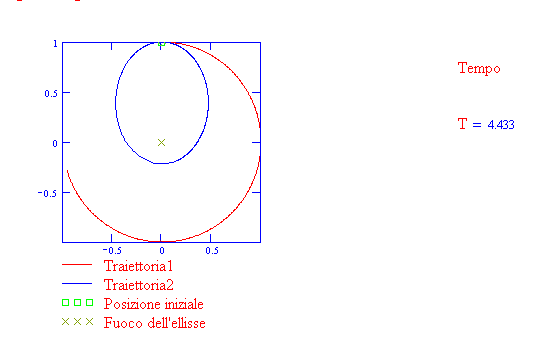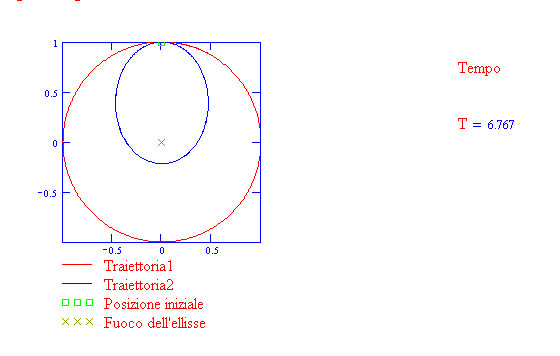


Riordina le tessere numerate secondo l’ordine naturale 1, 2, 3, … (con l’1 nella casella in alto a sinistra), facendo click su quella che vuoi spostare. Puoi selezionare uno schema dall’elenco in basso.
 |
Punti di Derivabilità o non delle Curve |
 |
Test sui punti estremanti (C.Elce) |
 |
Studio di Punti Singolari per le Curve |
Carlo Elce
 |
Test sulle conoscenze relative alla Terra nel Sistema Solare |
 |
Test sulle conoscenze relative alla Terra nel Sistema Solare |
Carlo Elce
 |
Ricerca di una funzione a partire da una sua primitiva (Carlo Elce) |
 |
Ricerca di una funzione a partire da una sua primitiva (Carlo Elce) |
 |
Test sul Moto dei Corpi |
 |
Test sui moti qualsiasi (C.Elce) |
Carlo Elce
Carlo Elce
 |
Elementi di Calcolo Vettoriale e Lavoro compiuto da una Forza |
 |
Interpretazione grafica di alcuni limiti Carlo Elce |
 |
Interpretazione grafica di alcuni limiti Carlo Elce |
 |
GRANDEZZE FISICHE ED ERRORI |
Carlo Elce
 |
Test sulle conoscenze relative al Moto Armonico Semplice |
Carlo Elce
 |
Test sugli asintoti delle funzioni (C.Elce) |
Carlo Elce
Carlo Elce
Algebriche
 |
Test sui domini delle funzioni
|
 |
Test sull’Elettricità e il Magnetismo Carlo Elce |
 |
Formule relative ad alcuni solidi Aree e Volumi |
 |
Test sullo Sviluppo in Serie di Potenze delle Funzioni |