 |
Il cortile Un cortile rettangolare può essere coperto con mattoni quadrati di 50 cm di lato. Tutti i mattoni sono interi e coprono completamente il cortile. L’architetto ha fatto comprare metà mattoni verdi e metà grigi. Li può disporre in due modi, mettendo i grigi al centro e i verdi ai bordi o viceversa i verdi al centro e i grigi ai bordi. Il bordo ha sempre la stessa altezza in tutti e quattro i lati del rettangolo. Quale area minima può assumere un cortile di questo tipo? Fatto un po’ di calcoli? Controlla la soluzione
|
Siano M il numero totale di mattoni, x il numero di mattoni dell’altezza, y il numero di mattoni della base, z il numero dei mattoni dello spessore del bordo. M=x*y.
Uguagliando l’area esterna con l’area interna si ha 2yz+2z(x-2z) = (x-2z)(y-2z);
da cui, esplicitando y= (4zx-8z2 )/(x-4z).
M=x*y=(4zx2 -8z2 x)/(x-4z). Si tratta di studiare il minimo assoluto di questa funzione in due variabili.
Poiché x, y, z devono essere numeri interi, si può vedere se esiste una soluzione per z=1.
M=4n(n-2)/(n-4). Si tratta, ora, di cercare un minimo assoluto e intero di questa funzione.
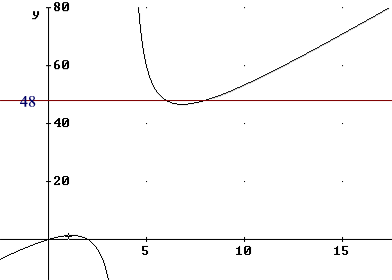 |
M ha un minimo per n = 4+\/8 circa 6,82.
|
