La dilatazione volumica
Anche i liquidi (quasi tutti) se riscaldati subiscono una dilatazione; anche in questo caso, è possibile ricavare una legge sperimentale che fornisce l’entità di tale variazione, e tale legge è la stessa che viene utilizzata nel caso dei solidi:
$V = V_0 * (1 + α * ∆t)$
Da notare, però, che la dilatazione che subiscono i liquidi quando riscaldati è notevolmente maggiore di quella subita dai solidi; infatti, il coefficiente di dilatazione volumica α nel caso dei liquidi è dalle 10 alle 100 volte maggiore di quello di un solido.
C’è, però, un liquido particolare il cui comportamento di discosta dal normale, e presenta importanti caratteristiche: l’acqua.
Il caso dell’acqua
L’acqua presenta un comportamento anomalo.
Ad esempio, se mettiamo una bottiglia di vetro colma d’acqua in surgelatore, dopo un certo periodo di tempo troveremo la bottiglia rotta. Infatti, raffreddandosi l’acqua sotto forma di ghiaccio aumenta di volume, rompendo così la bottiglia di vetro.
Allo stato liquido, poi, da 0°C a 4°C il volume dell’acqua diminuisce se riscaldata, mentre a temperature maggiori si ha un aumento di volume regolare sotto riscaldamento.
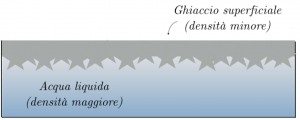
Queste caratteristiche dell’acqua possono spiegare come mai, in caso di temperature molto basse, notiamo uno strato di ghiaccio al di sopra di un recipiente d’acqua, o nel caso di un lago.
Nel caso di basse temperature, infatti, lo strato superficiale dell’acqua comincia a raffreddare e, di conseguenza, diminuisce il suo volume. Come sappiamo, una diminuzione di volume comporta un aumento della densità dello strato superficiale che, quindi, per le leggi di Archimede, tende a scendere verso il basso, permettendo all’acqua più calda che si trova in fondo di risalire verso l’alto.
Questo processo si ripete in continuazione, fino a quando tutta l’acqua non raggiunge una temperatura omogenea, supponiamo di 4°C.
Sotto tale temperatura, come abbiamo visto in precedenza, se raffreddata l’acqua aumenta di volume.
Di conseguenza, poiché lo strato superficiale è continuamente sottoposto a raffreddamento dall’ambiente esterno, si ha ora un aumento del volume di esso, con conseguente diminuzione della sua densità.
A questo punto, essendo lo strato superficiale meno denso dell’acqua sottostante, esso tende a rimanere in superficie; il continuo raffreddamento fa si che questo strato passi dallo stato liquido a quello solido, con formazione di ghiaccio superficiale.
Queste particolari caratteristiche dell’acqua sono dovute ai legami intramolecolari delle sue particelle; i legami presenti, infatti, sono legami idrogeno, che conferiscono alla struttura molecolare dell’acqua solida una forma più regolare e geometrica rispetto all’acqua allo stato liquido.
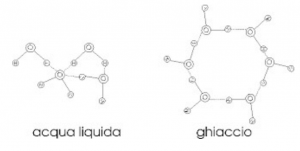
Questo spiega perché, a differenza della maggior parte delle sostanze, lo stato solido dell’acqua presenta una densità minore rispetto a quella dello stato liquido; questa caratteristica è evidente, e spiega perché il ghiaccio può galleggiare sull’acqua.
Esercizio
Un cilindro di ferro con area di base di $30,0 cm^2$ contiene dell’olio per un volume di $300 cm^3$, che viene compresso da un pistone. Il coefficiente di dilatazione volumica dell’olio è di $ 7,2 * 10^-4°C^(-1)$. Il recipiente viene riscaldato da 50°C a 150°C.
Calcolare l’aumento di volume dell’olio, e determinare di quanto si alza il pistone a causa dell’aumento dell’olio.
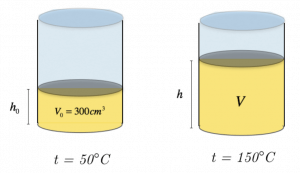
Per prima cosa, esprimiamo le grandezze nelle giuste unità di misura; abbiamo, quindi:
$A_b = 30 cm^2 = 30 * 10^(-4) m^2$
$V_0 = 300 cm^3 = 300 * 10^(-6) m^3$
Per determinare l’aumento di volume dell’olio, possiamo utilizzare la legge di dilatazione volumica, trovando così il volume finale del liquido:
$V = V_0 * (1 + α * ∆t) = 300* 10^(-6) * [1 + 7,2 * 10^(-4) * (150 – 50)] = 321,6 * 10^(-6) m^3$
Calcoliamo l’aumento di volume ∆V come differenza tra il volume finale e quello iniziale:
$∆V = V – V_0 = 321,6 * 10^(-6) – 300 * 10^(-6) = 21,6 * 10^(-6) m^3 = 21,6 cm^3$
Per rispondere al secondo quesito, calcoliamo l’altezza che raggiunge il livello dell’olio all’interno del cilindro prima e dopo la variazione della temperatura. Per ottenere il valore dell’altezza, dividiamo il volume occupato dall’olio per l’area di base del cilindro; nel primo caso abbiamo:
$h_0 = frac(V_0)(A_b) = frac(300 * 10^(-6) m^3)(30 * 10^(-4) m^2) = 0,1 m$
nel secondo caso, dopo l’aumento di temperatura:
$h = frac(V)(A_b) = frac(321,6 * 10^(-6) m^3)(30 * 10^(-4) m^2) = 0,1072 m$
La variazione di altezza si ottiene dalla differenza delle misure nei due casi:
$h – h_0 = 0,1072 – 0,1 = 0,0072 m = 0,72 cm$
Potrebbero interessarti
Appunti: La dilatazione dei solidi
