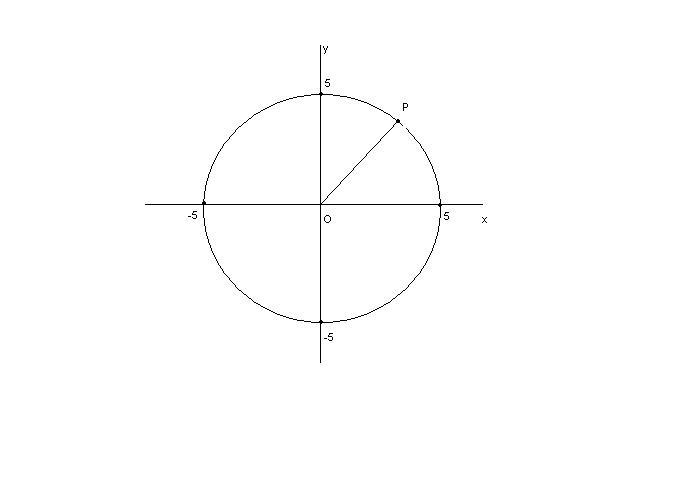
Determinare le coordinate del centro e il raggio della circonferenza avente la seguente equazione:
$x^2+y^2-6x-4sqrt2y+1=0$
Svolgimento
l’equazione della circonferenza di centro $(x_0;y_0)$ e di raggio $r$, sarà:
$(x-x_0)^2+(y-y_0)^2=r^2$
Sviluppandola si ha:
$x^2+x_0^2-2xx_0+y^2+y_0^2-2yy_0=r^2$
ponendo $-2x_0=\alpha$, $-2y_0=\beta$ e $x_0^2+y_0^2-r^2=\gamma$ si ha
$x^2+y^2+\alphax+\betay+\gamma=0$
che rappressenta l’equazione normale o canonica della circonferenza.
Il centro $C$ della circonferenza rappresentata dall’equazione canonica si ricava dalle due relazioni:
$\{(-2x_0=\alpha),(-2y_0=\beta):} => \{(x_0=-(\alpha)/2),(y_0=-(\beta)/2):}$;
Quindi $C(-(\alpha)/2; -(\beta)/2)$.
La misura del raggio invece si ricava dalla terza relazione
$r^2=x_0^2+y_0^2-\gamma => r^2=(-(\alpha)/2)^2+(-(\beta)/2)^2-\gamma => r=sqrt((-(\alpha)/2)^2+(-(\beta)/2)^2-\gamma)$.
Prendiamo in considerazione la nostra equazione
$x^2+y^2-6x-4sqrt2y+1=0$
Consideriamo l’equazione normale della circonferenza generica di raggio r e centro $C(x_0;y_0)$ si ha:
$\alpha=-6, \beta=-4sqrt2, \gamma=1$.
Pertanto, essendo $C(-(\alpha)/2; -(\beta)/2)$, otteniamo
$C(3;2sqrt2)$
ed essendo $r=sqrt((-(\alpha)/2)^2+(-(\beta)/2)^2-\gamma)$ si ha
$r=sqrt((3)^2+(2sqrt2)^2-1)=sqrt(9+8-1)=sqrt(16)=4$.




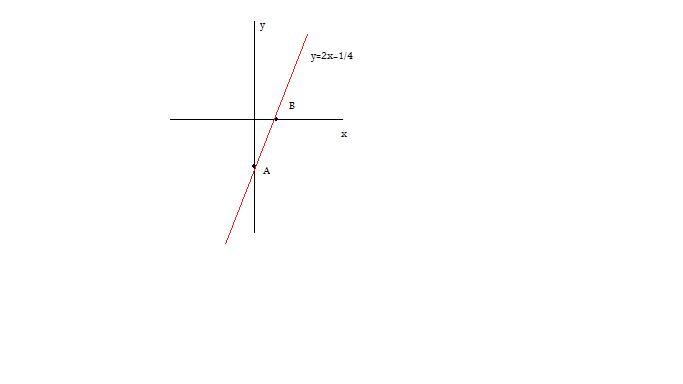
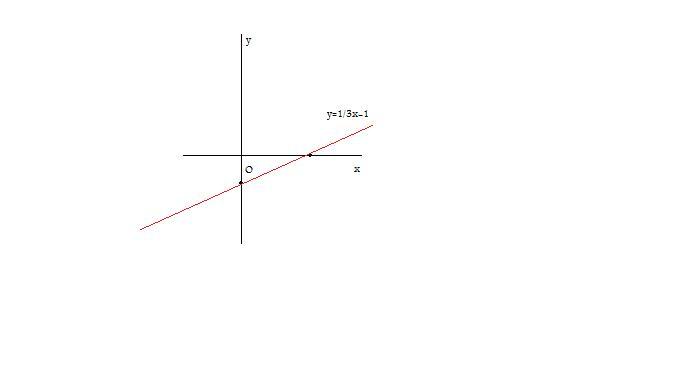
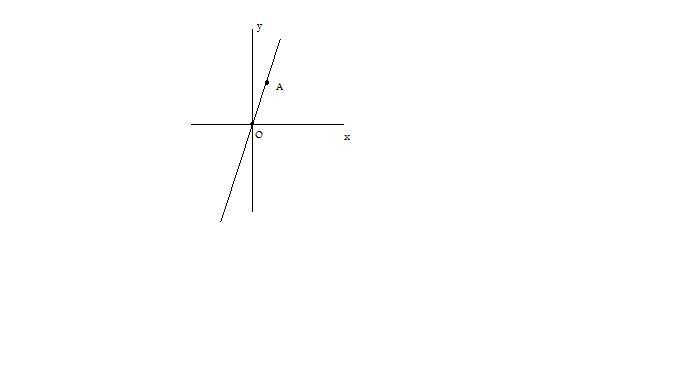
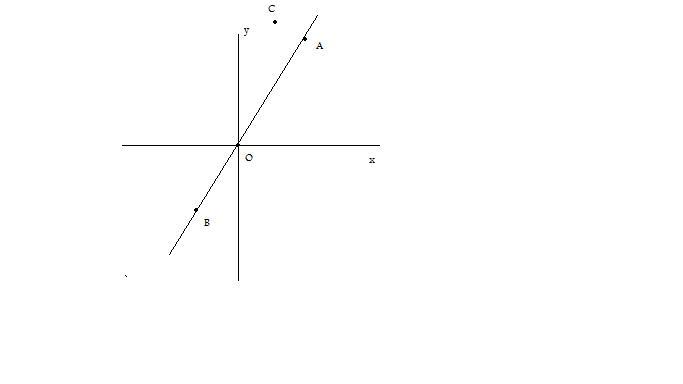 La retta $r$, passando per l’origine, sarà rappresentata da un’equazione del tipo $y=mx$.
La retta $r$, passando per l’origine, sarà rappresentata da un’equazione del tipo $y=mx$.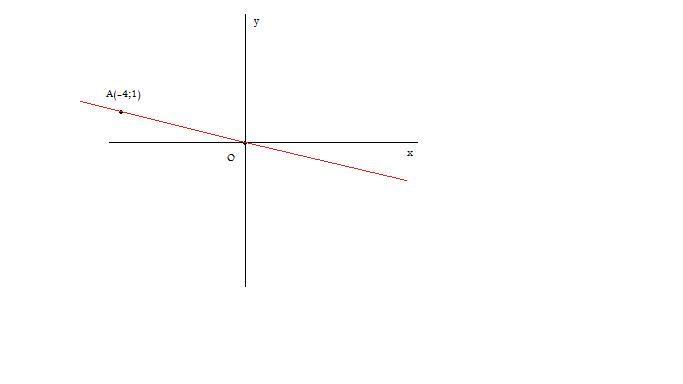
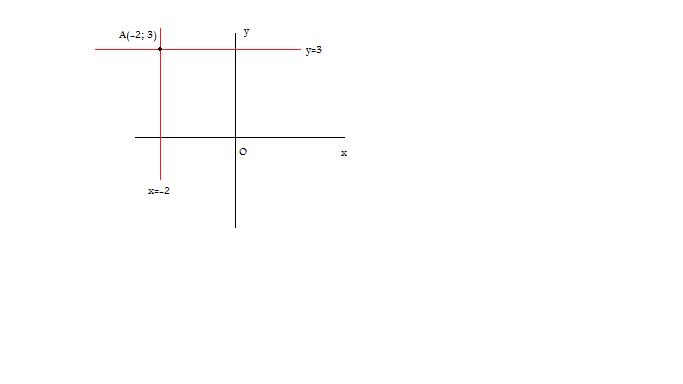 Come è evidente dalla figura le equazioni richieste sono:
Come è evidente dalla figura le equazioni richieste sono: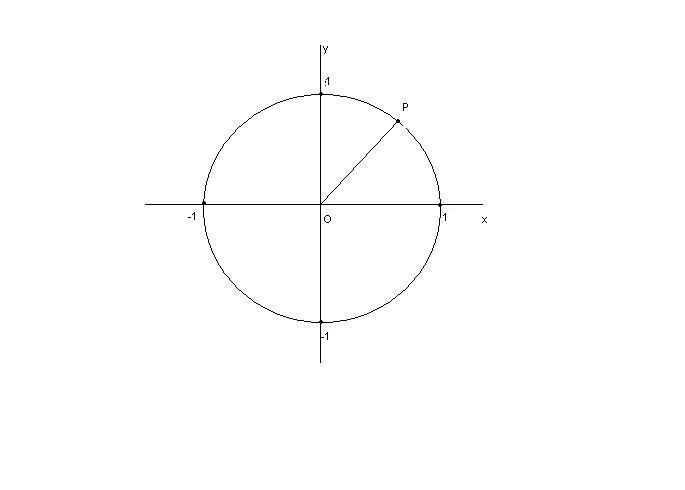 I punti appartenenti a questa circonferenza sono quelli aventi distanza dall’origine pari a $1$,
I punti appartenenti a questa circonferenza sono quelli aventi distanza dall’origine pari a $1$,