In questo lavoro propongo ai docenti della scuola secondaria di primo e secondo grado, l’esplorazione e lo studio di due prove rilasciate dall’indagine internazionale OCSE PISA, col software libero di geometria dinamica GeoGebra.
Introduzione
Tra le prove rilasciate [4] dalle indagini internazionali PISA (Programme for International Student Assessment), promosse dall’Organizzazione per la Cooperazione e lo Sviluppo Economico (OCSE), per misurare i livelli di competenze (literacy) dei quindicenni scolarizzati in lettura, matematica e scienze, alcune, possono costituire delle semplici attività laboratoriali da realizzare col software di geometria dinamica in breve tempo. Presenterò due degli items che sono stati oggetto di analisi e discussione nei lavori di gruppo dei seminari di informazione e sensibilizzazione promossi da MIUR e INVALSI, rivolti ai docenti della scuola secondaria di secondo grado delle regioni dell’obiettivo convergenza (Calabria, Campania, Puglia e Sicilia) e nell’ambito del piano nazionale m @ t.abel, di cui sono docente tutor. In questi contesti oltre a presentare i quadri di riferimento teorici e i risultati conseguiti dagli studenti si è discusso di sui programmi didattici ministeriali italiani, sulla valutazione (cosa e come valutano le indagini internazionali rispetto a cosa e come si valuta a scuola) e sulla opportunità di utilizzare questa tipologia di quesiti nella prassi didattica.
Si rimanda alle pubblicazioni riportate in bibliografia e sitografia per trattazioni approfondite sull’indagine OCSE PISA. Informazioni utili sulle altre indagini internazionali sono reperibili anche sul sito dell’INVALSI [1].
Ricordo solo che la Mathematical Literacy in PISA è definita come: “la capacità di un individuo di individuare e comprendere il ruolo che la matematica gioca nel mondo reale, di operare valutazioni fondate e di utilizzare la matematica e confrontarsi con essa in modi che rispondono alle esigenze della vita di quello individuo in quanto cittadino impegnato, che riflette e che esercita un ruolo costruttivo.”
Uno degli elementi principali che concorre alla valutazione della literacy in matematica è il processo di matematizzazione. I quesiti proposti, sono sempre ambientati in un contesto reale e spesso i quindicenni italiani, non li riconoscono come “problemi di matematica”, perché molto diversi dalla maggior parte degli esercizi e problemi di routine presenti nei libri di testo, da qui, la necessità di abituare gli studenti ad utilizzare le conoscenze acquisite in contesti meno strutturati.
Problema 1: Area di un continente
Questo problema fornisce come stimolo iniziale la carta geografica dell’Antartide con la relativa scala (vedi [5], pag. 79).
Domanda: AREA DEL CONTINENTE
Stima l’area dell’Antartide utilizzando la scala della carta geografica. Mostra il tuo lavoro e spiega come hai fatto la tua stima. (Puoi disegnare sulla carta se questo può aiutarti a fare la tua stima). …………………………………………………………………………………………………………………. …………………………………………………………………………………………………………………. ………………………………………………………………………………………………………………….
L’item appartiene all’area di contenuto: spazio e forma. Nell’indagine si attribuiva il punteggio pieno 712 (Livello 6 sulla scala complessiva di literacy in matematica, cioè il livello delle eccellenze) per la risposta corretta: area compresa fra 12.000.000 e 18.000.000 km², utilizzando una o più figure con cui approssimare la superficie dell’Antartide.
Il punteggio parziale 629 (corrispondente al Livello 5 sulla scala complessiva di literacy in Matematica) veniva assegnato se lo studente utilizzava un metodo corretto, ma la risposta era incompleta o errata. Tra le note esplicative, si precisava che anche un semplice tracciato sulla mappa veniva valutato come una spiegazione. L’obiettivo non era quello di testare le capacità espressive a livello lessicale, ma di capire come lo studente giungeva a dare la sua risposta.
Un simile quesito, considerando l’ampio spazio che viene dato allo studio delle proporzioni nella scuola italiana, a partire dalla scuola secondaria di primo grado, non avrebbe dovuto mettere in difficoltà gli studenti, invece la percentuale di risposte esatte per l’Italia è stata bassissima, pari al 3,9% (media OCSE: 9,4%). Le risposte parzialmente corrette dell’Italia sono state pari al 7,4% (media OCSE: 19,1%), il 9% delle risposte italiane sono state errate (media OCSE: 19,7%), altissimo è stato il numero di omissioni dell’Italia 73,3% (media OCSE: 48,2%), mentre il 6,4% non ha raggiunto il quesito perché in fondo al fascicolo (media OCSE: 3,7%).
Dalle discussioni con i colleghi, è emerso che, risultati così deludenti possano sensibilmente migliorare, proponendo di tanto in tanto agli studenti di fornire delle stime quali: l’altezza di un palazzo, le dimensioni dell’aula o della palestra scolastica, la superficie di un territorio di cui si ha una carta geografica o una mappa catastale, poiché tali competenze sono essenziali nella vita quotidiana.
Per rendere più interessanti simili esercizi, suggerisco di far scaricare agli studenti delle carte geografiche o immagini dal Web, acquisirle nel foglio lavoro del software libero GeoGebra per stimare superfici, dimensioni o la lunghezza di percorsi.
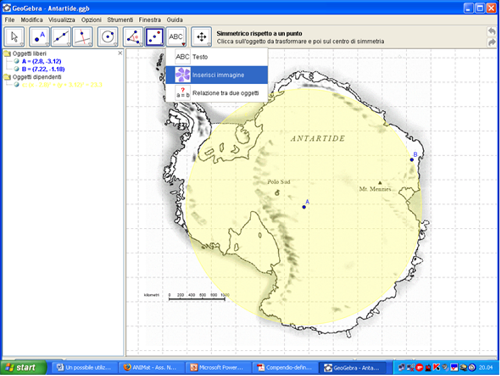
In figura 1 ho acquisito la cartina dell’Antartide: dall’icona n.8 “Testo” basta selezionare “Inserisci immagine”, poi cliccando nel foglio di lavoro, si apre una finestra di dialogo che consente di selezionare il percorso dell’immagine prescelta. Una volta acquisita, l’immagine può essere selezionata e trascinata nel punto desiderato e, cliccando su di essa col tasto destro del mouse, selezionando “Proprietà”, può essere posta in secondo piano, come immagine di sfondo. Con un clic col tasto destro del mouse nel foglio di lavoro, è possibile deselezionare e nascondere gli assi cartesiani e visualizzare la griglia. In questo modo si può far calcolare l’area approssimandola per eccesso o per difetto in diversi modi.
Problema 2: Il lampione
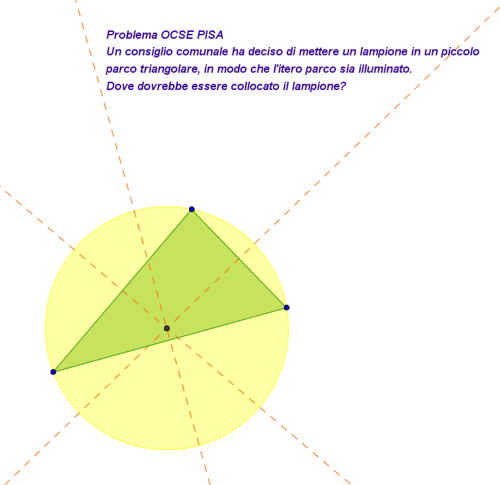
Il consiglio comunale ha deciso di mettere un lampione in un piccolo parco triangolare in modo che l’intero parco sia illuminato. Dove dovrebbe essere collocato il lampione?
Il testo di questo problema (vedi [6] a pag.31), inizialmente ha suscitato in me diverse perplessità per la sua genericità, ma, i colleghi con cui ho discusso, hanno dimostrato di apprezzarlo molto, per cui mi sono convinta che possa fornire utili spunti di discussione in classe.
Il problema è ambientato in un contesto di vita pubblica. Gli studenti lo devono modellizzare utilizzando degli enti geometrici. Successivamente, devono risolvere il problema matematico e verificare quali soluzioni risolvano anche il problema reale. In figura 2 ho costruito un triangolo con GeoGebra, ho determinato il circocentro e ho disegnato la circonferenza circoscritta al triangolo. Attraverso l’esplorazione col software di geometria dinamica, gli studenti possono verificare che se il parco ha la forma di un triangolo ottusangolo, il lampione non può essere collocato nel parco e se il triangolo è rettangolo, il lampione andrebbe collocato nel punto medio dell’ipotenusa, quindi sul bordo del parco. Questa attività con GeoGebra è stata ritenuta dai colleghi un’utile applicazione da proporre in classe quando si studiano i punti notevoli dei triangoli.
E’ opportuno, tuttavia, che per realizzarla, l’insegnante riduca i menù, in modo che gli studenti abbiano a disposizione solo le funzioni che dovranno utilizzare (ad esempio è opportuno che costruiscano gli assi senza utilizzare direttamente lo strumento “Asse di un segmento”). Per far questo è sufficiente selezionare dal menù “Strumenti”, “Personalizza barra degli strumenti” e rimuovere gli strumenti non necessari. GeoGebra dispone inoltre di una barra di navigazione, per visualizzare i passi di una costruzione già salvata e il protocollo di costruzione. Selezionare “Barra di Navigazione per i passi di costruzione” nel menu “Visualizza” per visualizzare la barra di navigazione in fondo alla finestra geometria.
Bibliografia
OCSE: PISA 2003 valutazione dei quindicenni : quadro di riferimento : conoscenze e abilità in matematica, lettura, scienze e problem solving, Armando Editore, Roma 2004.
INVALSI: Rapporto nazionale OCSE-PISA 2003, Il livello dei quindicenni italiani in matematica, lettura, scienze e problem solving,Armando Editore, Roma 2006.
INVALSI :Rapporto nazionale OCSE PISA 2006 Le competenze in scienze lettura e matematica degli studenti quindicenni, Armando Editore, Roma 2008.
OCSE: Valutare le competenze in scienze, lettura e matematica, Quadro di riferimento di PISA 2006, Armando Editore, Roma 2007.
Sitografia
Il sito dell’INVALSI:
[1] www.invalsi.it
Sito ufficiale OECD:
Le indagini OCSE:
[3] http://www.invalsi.it/invalsi/ric.php?page=intocse
Le prove rilasciate e altri documenti:
[4] http://www.invalsi.it/invalsi/ri/sito/pagine/documentazione.htm
in questa pagina l’item “Area di un continente” è reperibile all’indirizzo:
[5] http://www2.invalsi.it/RI/pisa2006/docs/ProvePISA2000.pdf
[6] Sempre all’indirizzo [4], è reperibile il problem solving: Il Lampione cliccando sul link: Valutazione dei quindicenni. Quadro di riferimento: conoscenze e abilità in matematica, lettura, scienze e problem solving
Alcuni articoli reperibili in rete:
[7] https://www.matematicamente.it/magazine/gennaio2008/Bernardo-Vitiello-Indagine_Pisa_2006.pdf
[8] http://www.treccani.it/Portale/sito/scuola/in_aula/matematica/OCSE_PISA/mainArea.html
[9] http://www.matematica.it/paola/progettoalicepisa.pdf
Il software Geogebra si può scaricare liberamente dal sito:
[10] http://www.geogebra.org/cms/index.php?lang=it
[11] Una miniguida di GeoGebra
Allegati
Antartide.ggb (figura 1)
Lampione.ggb (figura 2)
Scarica l’articolo completo Prove Pisa e Geogebra
Alessandro può trovare le prove rilasciate di lettura ai link:
http://www2.invalsi.it/RI/pisa2006/docs/ProvePISA2000.pdf da pag.2 a pag.72
ho bisogno di una copia di un esempio di prova di italiano.
grande Rosa :-))
Conoscete il Prof Adolfo Schilardi….. Lui è un fissato di queste indagini .
Vorrei fare una piccola osservazione sul II problema: in realtà il problema matematico è leggermente diverso dal problema pratico, in quanto nel caso in cui il triangolo è ottusangolo, il lampione conviene metterlo all’interno, nonostante non coincida con il circocentro: non si chiede che il lampione sia equidistante dai vertici, ma (credo) che l’illuminazione sia la migliore possibile…
Come già detto nel testo, possono esserci spunti per discussioni interessanti in aula e questo ne è un esempio.