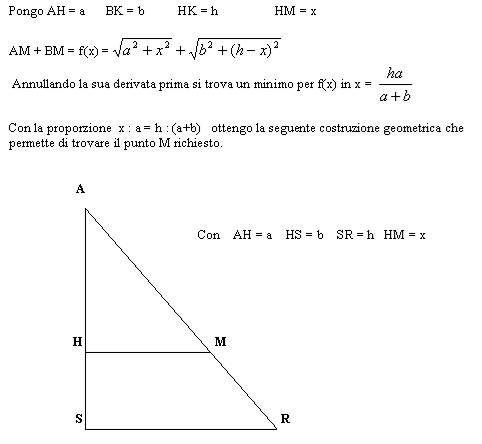 |
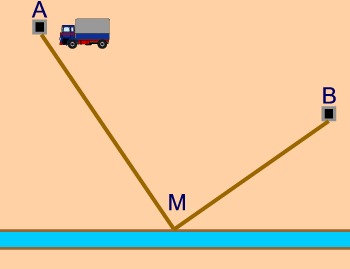
Autobotte Un'autobotte deve riempire i pozzi A e B da un canale, come nel disegno. Parte da A riempie la botte dal canale, scarica l'acqua in B, ritorna al canale, riempie la botte e scarica l'acqua in A. Da quale punto M conviene che carichi l'acqua? Dare la soluzione con una costruzione geometrica. |
Matrix (Teramo)

Franz Kafka (Carpi)
Indichiamo con B' il punto simmetrico di B rispetto alla retta individuata dal canale. Deve essere minima la distanza complessiva AM+MB+BM+MA. Dato che B e B' sono simmetrici, in pratica deve essere minima la distanza AM+MB'. Tale distanza è minima quando i tre punti A, M, B' sono allineati.
Dunque dovrà essere AMC = C'MB', essendo due angoli opposti al vertice. Per simmetria dovrà quindi essere AMC=CMB. La posizione di M è quindi quella per la quale l'angolo di incidenza è uguale a quello di riflessione (È il principio di Fermat).
Cavia (Castelvetro MO)
Il punto M è quello …
1) … che divide il segmento delle proiezioni di A e B sulla retta del fiume in parti direttamente proporzionali alle distanze di A e B dal fiume;
2) … per il quale la perpendicolare per M alla retta del fiume è bisettrice dell'angolo AMB;
3) … che si ottiene congiungendo A con il simmetrico B' di B rispetto alla retta del fiume (retta della sponda del fiume dalla parte di A e B!)
Ucando (Gallarate VA)
Supponiamo di trasferire il problema in un asse cartesiano. I punti A, B, M hanno le coordinate:
A ( 0 ; Ya )
B ( Xb ; Yb)
M ( Xm, 0 )
La richiesta consiste nel minimizzare la somma di AM e BM; senza scrivere la formula con il teorema di Pitagora, indicherò con f(x) la funzione AM + BM. Occorre, per calcolare il punto di minimo di f(x), calcolare la derivata prima f ' (x) e porla = 0. Si arriva alla soluzione Xm= (Xb * Ya)/(Yb+Ya)
con Xm la nostra incognita (perchè si deve decidere in quale punto attingere acqua dal canale, e questo risiede sull'asse delle ascisse). E' da notare che il numeratore della soluzione (Xb * Ya) corrisponde
all'area del rettangolo circoscritto ai tre punti.
Emy e Max (Torino)
Secondo me si può risolvere (per tentativi) attraverso un'ellisse: prendiamo la classica corda i cui estremi fissiamo in A e B, il luogo dei punti ottenuti tendendo la corda con una matita è notoriamente un'ellisse; se la corda è troppo lunga, l'ellisse taglierà in due punti il canale; riducendo dunque la lunghezza della corda fino a quando la nuova ellisse è tangente al canale, individuo sia il punto M (è il punto di tangenza) che la distanza A-M-B (che è la lunghezza della corda).
Roberto (Roma)
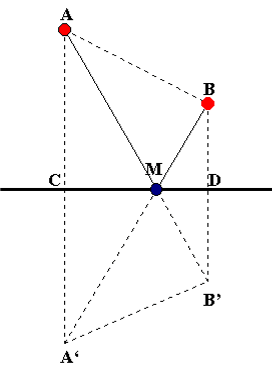
| La soluzione viene rappresentata nella costruzione geometrica riportata nel disegno allegato. In esso si vede che il punto M è il punto di incrocio delle due diagonali del trapezio isoscele ABB'A' avente come asse di simmetria la retta CD rappresentativa del canale. Infatti il percorso minimo dell'autobotte è equivalente al segmento di linea retta AB' = AM + MB' = AM + MB in un verso e al segmento di linea retta BA' = BM + MA' = BM + MA nell'altro verso. |
 |
Amelia (Milano)