 |
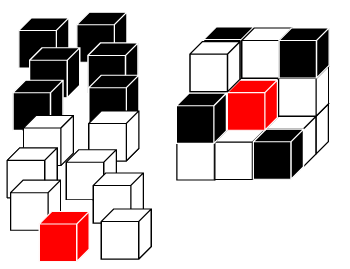
Un cubo particolare 27 cubetti colorati (1 rosso, 13 bianchi, 13 neri) vanno incollati per formare un cubo più grande. Quanti cubi di questo tipo si possono ottenere? |
La soluzione più completa pervenutami è, a mio giudizio, quella di Leon (Ercole Suppa) Teramo.
Ne riporto una sintesi significativa
LEMMA 1. Un cubo soddisfacente le condizioni richieste ha su ogni faccia 5 o 4 quadrati neri.
DIMOSTRAZIONE. Sia C un cubo avente su ogni faccia k quadretti neri; k deve essere minore o uguale a 6, altrimenti i cubetti neri posti su due facce opposte sarebbero più di 13. Supponiamo per assurdo che k=6. Dividiamo il cubo grande in tre strati. Poiché sugli strati superiore e inferiore vi sono 12 cubetti neri, nello strato intermedio vi è un solo cubetto nero. Il medesimo ragionamento si può ripetere per gli altri due strati centrali. Pertanto complessivamente nell’unione dei tre strati centrali vi possono essere al massimo 3 cubetti neri e gli altri 10 cubetti neri dovrebbero appartenere al complementare. Ma ciò è impossibile il quanto il complementare ha solo 8 elementi (gli otto vertici del cubo). Non può essere k<= 3 altrimenti su ogni faccia vi sarebbero h=9-k quadrati bianchi, ma e ciò è impossibile per quanto provato nella prima parte dato che h>=6.
LEMMA 2. Le soluzioni con 5 quadretti su ogni faccia sono tante quante quelle con 4 quadretti.
DIMOSTRAZIONE. Basta osservare che i cubi con quattro quadretti neri su ogni faccia sono in corrispondenza biunivoca con i cubi aventi cinque quadretti bianchi su ogni faccia.
In virtù dei due lemmi precedenti basta contare in quanti modi può essere costruito un cubo con 5 quadrati neri su ogni faccia (il doppio di tale numero è la soluzione richiesta). Esaminando tutti i casi possibili (con metodo "brute force") ho trovato che vi sono 4980 soluzioni. La parte più difficile è stata quella di contare quante sono le soluzioni effettivamente distinte. A tal fine ho utilizzato il seguente

Nel problema in questione:
· X è l’insieme delle colorazioni di un cubo 3×3 associate a tutte le possibili costruzioni del cubo con i 27 cubetti (in modo che ogni faccia presenti 5 quadrati neri).
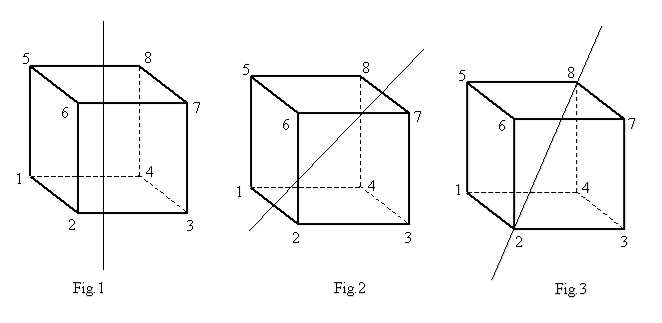
· G è il gruppo delle simmetrie del cubo. G ha 24 elementi, precisamente:
a) 9 rotazioni intorno intorno ad una retta passante per i centri di due facce opposte (vi sono tre scelte per le coppie di facce opposte e, per ogni scelta tre rotazioni diverse dall’identità, ossia di 90°, 180°, 270° ) . [Fig. 1]
b) 6 rotazioni di 180° intorno ad una retta passante per i punti medi di due spigoli diagonalmente opposti. [Fig. 2]
c) 8 rotazioni intorno ad una retta passante per due vertici diagonalmente opposti (vi sono quattro scelte per tali rette e, per ogni scelta due rotazioni diverse dall’identità, ossia di 120° e 240°). [Fig. 3]
d) l’identità.
La soluzione completa è scaricabile da questo link
Contiene
1)cubo particolare.doc = documento word in cui è descritto il procedimento risolutivo
2)cubo.pas=programma scritto in turbo pascal utilizzato per implementare l’algoritmo risolutivo
3)cubo.exe=eseguibile di cubo.pas, lanciabile direttamente da windows
4)fdelay.tpu=libreria per tp7 (Necessaria solo se si vuole far girare il programma dall’ambiente di sviluppo del tp7, su computer pentium. Essa va copiata nella cartella BP/UNITS. Non necessaria su computer 486 o inferiore).
Il programma allegato CUBO.EXE , oltre al numero di modelli di cubi soddisfacenti i requisiti richiesti, determina anche i modelli stessi (che vengono visualizzati a video) e le classi di equivalenza.
La soluzione di F15-eagle S. Giorgio su Legnano (MI)
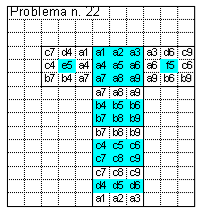
STEP 1
Con riferimento al cubo "aperto", le caselle NON colorate di azzurro rispettano le premesse del problema (le facce del cubetto sullo spigolo devono avere necessariamente lo stesso colore).
Partendo da una faccia qualsiasi (ex. A), tutte le altre facce devono rispettare le premesse e, pertanto, la faccia B ha bloccate le tre facce adiacenti ad A, ma le altre sono necessariamente "libere", potendo assumere indifferentemente il valore 0 o 1 (bianco, nero). Analogamente per le successive facce C, D, E, F. E’ chiaro che, in questo modo, si individuano TUTTE le possibili disposizioni di 0 e 1 che rispettano SOLTANTO le premesse sul colore uguale delle facce dei cubetti sugli spigoli.
STEP 2
Per rispettare la premessa di un numero uguale di facce "piccole" su ciascuna faccia "grande" del cubo, si devono individuare soltanto quelle con 4 facce "piccole" di color nero (quelle con 5 sono la soluzione complementare), poiché è l’unico caso che permette di rispettare anche la premessa di pari numero (13) di cubetti bianchi e neri. E’ chiaro che, in questo modo, si individuano TUTTE le possibili disposizioni di 0 e 1 (bianco, nero) che rispettano SOLTANTO le premesse sul numero uguale di facce "piccole" con ugual colore su ciascuna faccia "grande", includendo tutti i "doppioni" ottenibili per rotazione.
Il numero di disposizioni così ottenute è 4980.
STEP 3
A questo punto, è necessario individuare i "doppioni". La procedura, lunga e laboriosa consiste nel considerare CIASCUNA
disposizione ottenuta al precedente STEP 2, farle assumere TUTTE le possibili rotazioni (0°, 90°, 180°, 270°) in TUTTE le possibili facce (ossia, prima come se si trovasse sulla faccia A, poi sulla B, ecc., fino alla F) e, PER CIASCUNA NUOVA SITUAZIONE, confrontarla con TUTTE le altre disposizioni calcolate al precedente STEP 2.
Quando si individua un "doppione", esso viene codificato per poter essere eliminato.
Questo procedimento permette di analizzare TUTTE le possibili combinazioni di facce/rotazioni per ciascuna disposizione,
evitando così la possibilità di non individuare eventuali "doppioni".
Vedi l’elenco delle soluzioni
Leggi la soluzione di Matrix Teramo
Leggi le soluzioni di Robiwood Borgaro (TO)
La risposta di Dodos Ascoli Piceno
Il numero di cubetti dello stesso colore che può essere collocato su ogni faccia è 5 oppure 4.
Si ottengono le stesse configurazioni sia utilizzando 4 cubetti, sia utilizzandone 5, essendo due numeri reciprocamente complementari rispetto a 9.
E’ sufficiente cercare le configurazioni ottenibili con 5 cubetti e raddoppiare il risultato finale ottenuto.
Con l’uso di un programmino in Pascal, si simula il posizionamento dei 5 cubetti su ognuna delle 6 facce del cubo tenendo presente il vincolo dei 13 quadretti a disposizione e l’altro vincolo costituito dal fatto che alcuni cubetti appartengono contemporaneamente a 2 o a 3 facce.
L’elaborazione fornisce il risultato di 4980 configurazioni possibili.
Sorge poi l’ostacolo più serio che consiste nell’individuare, all’interno del valore ottenuto, quante siano quelle configurazioni che sono da scartare in quanto rappresentano uno degli altri possibili 23 modi di osservare (ruotandolo) il cubo grande ottenuto.
Affinando il programma precedente si ottiene il valore di 227.
Quindi:
227 cubi con 5 cubetti neri per faccia;
227 cubi con 4 cubetti neri per faccia.
454 cubi complessivi.
La soluzione di Shuty Genova
Le soluzioni possono avere 4 o 5 quadrati neri sulle facce del cubo. Ovviamente, per ragioni di simmetria (le soluzioni con 4 quadrati neri sono anche soluzioni con 5 quadrati bianchi e viceversa) il numero di soluzioni dei 2 tipi è lo stesso, cioè 227.
Innanzitutto ho elaborato un semplice programmino che calcolasse tutte le soluzioni, senza in un primo momento considerare le possibili simmetrie del cubo, cioè trascurando il fatto che due soluzioni potessero essere ottenute dallo stesso cubo ruotato in maniera diversa.
Nel file allegato in Excel, "Sol-inviate ", foglio "Soluzioni", trovate tutte le soluzioni trovate, sono 9960, 4980 con 4 quadrati neri ed altrettante con 5. Nel file PowerPoint, "Cubo – disegno ", trovate la convenzione utilizzata per numerare le 27 posizioni dei cubetti componenti, mentre nel file Excel il numero 1 indica il cubetto nero, mentre lo 0 il cubetto bianco in ciascuna
delle 27 posizioni possibili.
Successivamente ho considerato le rotazioni. Il cubo si può posizionare in 24 modi diversi, che si possono ottenere appoggiando il cubo su ciascuna delle 6 facce e ruotandolo 4 volte attorno ad un asse verticale: 6×4 = 24.
Ho quindi paragonato, sempre con un programmino, le soluzioni tra di loro per vedere quali non fossero ottenibili da rotazioni di una delle altre. Il risultato e’ di 227 soluzioni indipendenti per i 2 possibili tipi di soluzione (con 4 e 5 quadrati neri sulle facce). Nel file allegato in Excel, "Sol-inviate", foglio "Soluzioni scremate", trovate le 227 soluzioni nel caso di 4 quadrati
neri su ogni faccia (per quelle con 5 quadrati neri basta invertire gli 0 con gli 1)
Per la cronaca, le 227+227 soluzioni hanno in qualche caso delle simmetrie interne. Vi sono infatti 31+31 soluzioni con 2 simmetrie (cioè esistono 2 posizioni ruotate identiche), mentre ve ne sono 6+6 con 3 simmetrie.
La soluzione di Roberto (Pasquale Salemme) Roma
Si possono ottenere:
n. 227 cubi aventi per singola faccia 5 quadratini bianchi e 4 neri
n. 227 cubi aventi per singola faccia 4 quadratini bianchi e 5 neri
Infatti:
Si è riesaminato il problema e con riferimento ai cubi possibili ottenuti secondo i programmi in qbasic "Cub_1" e "Cub_2",
precedemente inviati, si è provveduto a scrivere un nuovo programma in qbasic abbastanza complesso con il quale vengono eliminati tutti i cubi equivalenti ottenendo i seguenti risultati riportati nella tabella suddivisi secondo le 5 tipologie dimostrate nei file precedentemente inviati.
Il programma in qbasic "Cubo ", riportato in allegato, elimina i cubi che si ottengono facendolo ruotare secondo le 24 posizioni che uno stesso cubo può presentarsi alla nostra vista.
Per cui rivedendo la tabella delle tipologie già inviata si ottiene:
5 bianchi e 4 neri per faccia————-4 bianchi e 5 neri per faccia
X—>Y—>Z—>Config.—->Cubi——–>X—>Y—>Z—>Config.—->Cubi
4—>9—>0—> 216———>15———->4—>3—>6—->216———>15
5—>7—>1–>1992———>83———->3—>5—>5—>1992——–>83
6—>5—>2–>2352——->109———->2—>7—>4—>2352——->109
7—>3—>3—->408——–>19———–>1—>9—>3—->408———>19
8—>1—>4—–>12———–>1———->0–>11—>2—–>12———–>1
——————————————————————————————–
Tot.———–>4980——–>227——–>Tot.—————>4980——->227
Si nota che l’ultima tipologia il cubo è unico.
La soluzione di Gino Gigliod’oro Rolo (RE)
motivazione: Ci sono tre tipi di cubi superficiali: 8 con tre facce visibili (t), 12 con due facce visibili (d) e 6 con una faccia visibile (u).
Il numero di facce visibili è dato in totale da f=3t+2d+u, con t+d+u=13, da cui f=2t+d+13.
Per (t,d,u) vi sono solo le seguenti possibilità:
(0,11,2), (1,9,3), (2,7,4), (3,5,5), (4,3,6) con 4 quadrati neri per ogni faccia del cubo e (4,9,0), (5,7,1), (6,5,2), (7,3,3), (8,1,4) con 5 quadrati neri per ogni faccia del cubo.
Rappresentando sullo sviluppo del cubo in corrispondenza di ciascun caso le varie combinazioni possibili, a meno di rotazioni, si arriva a 454 configurazioni diverse, nel senso che non si distinguono due cubi ottenibili l’uno dall’altro mediante un movimento. In alcuni casi la configurazione è unica o si ottiene con un semplice ragionamento di tipo combinatorio mentre in altri si rende necessario un conteggio diretto (almeno io ho dovuto fare così!).
Leggi le soluzioni di Ucando Gallarate (VA)
