 |
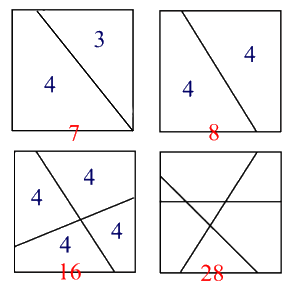
Dividere un quadrato Un segmento che congiunge due lati di un quadrato divide il quadrato in due poligoni. Nel primo caso disegnato i poligoni hanno rispettivamente tre lati e quattro lati. La somma dei lati dei due poligoni ottenuti è 7. Nel secondo caso, lo stesso quadrato è stato diviso da un segmento congiungente due lati in due poligoni di quattro lati. La somma dei lati dei poligoni in questo caso è maggiore, 8. Utilizzando 7 segmenti congiungenti due lati del quadrato, qual è il numero massimo di lati di poligoni ottenibile? |
La soluzione di Matrix Teramo
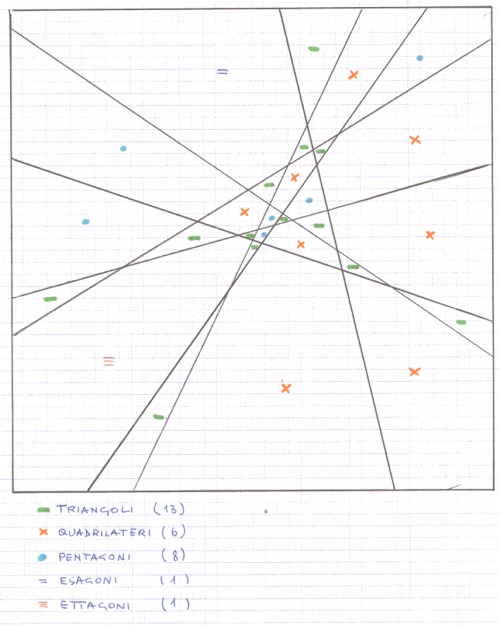
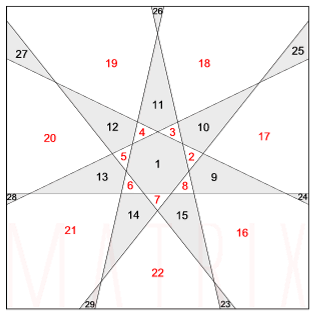
| Sono stati prolungati i 7 lati dell'ettagono regolare (1), fino al quadrato di contorno. In questo modo si ottengono 7 segmenti che generano il massimo numero di nodi interni (e quindi il massimo numero di poligoni). Ogni segmento, infatti, interseca gli altri sei, oltre naturalmente a due lati del quadrato.
Si ottengono quindi 29 poligoni: Il numero complessivo dei lati è pertanto 116. |
 |
L'idea di Giancod Roma
Ho trovato la seguente regola: se con K segmenti si ottengono al massimo N lati, con K+1 segmenti se ne ottengono al massimo N+4(K+1).
Per cui
K=1 –> N = 8.
K=2 –> N = 8 + 4x(2) = 16
K=3 –> N = 16 + 4x(3) = 28
…………………………………….
K=6 –> N = 64 + 4x(6) = 88
K=7 –> N = 88 + 4x(7) = 116
La generalizzazione di Leon Teramo
Generalizziamo il problema: qual è il numero massimo di lati dei poligoni ottenibili utilizzando n corde congiungenti due lati del quadrato (con n>=2). Il massimo si ottiene quando:
1) ogni corda interseca due lati del quadrato in due punti diversi dai vertici
2) ogni corda è intersecata in n-1 punti dalle rimanenti n-1 corde
Nella figura che si ottiene rispettando le condizioni 1), 2) i lati dei poligoni, giacenti sul contorno del quadrato originario, sono 2n+4 e vanno contati una sola volta; i lati dei poligoni , interni al quadrato sono n*n ma ognuno di essi dev'essere contato due volte. Pertanto il massimo numero dei lati di tutti i poligoni che si vengono a formare è
f(n) = 2n^2 +2n + 4 , per ogni n>=2 [ f(1)=8 ]
Per n=7 si ottiene f(7) = 116.
Una bella costruzione di Ucando Gallarate (VA)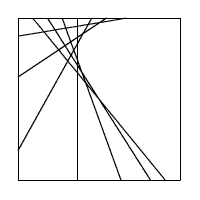
La suddivisione "artigianale" di Amelia Milano