Quadrati magici da 1 a 25
|
I quadrati magici hanno una storia millenaria. Da sempre sono stati visti come amuleti, oggetti mistici, soprannaturali. Oggi interessano poco sia ai cosiddetti maghi sia ai matematici di professione. Restano un oggetto di culto per la matematica curiosa, l’enigmistica e altro. Con i numeri 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25 costruire il maggior numero di quadrati magici, chiaramente di ordine 5. Due quadrati sono diversi se hanno almeno due numeri disposti in posizioni differente. Il punteggio sarà assegnato a chi troverà il maggior numero di quadrati magici.
|
Questo problema è piuttosto complesso. La soluzione completa del problema viene attribuita a Richard Schroeppel, che nel 1973 ha calcolato, con un programma al computer, tutti i quadrati magici possibili di ordine 5×5: sono 275.305.224, senza contare riflessioni e rotazioni. Ne ha dato notizia Martin Gardner nel n. 234 (1976) di Scientific American (notizia segnalatami da LEON ) e nell’edizione italiana Le Scienze del luglio 1976 (notizia segnalatami da MATRIX ). Nessuno e riuscito a trovare indicazioni precise dell’algoritmo usato da Scroeppel per risolvere il problema. Senza un buon algoritmo non si praticamente nessuna speranza di risolvere il problema.
Tra le soluzioni pervenutemi, quella di LEON contiene un algoritmo che rapidamente fornisce 52.992 quadrati magici distinti. Il punto viene quindi assegnato a LEON.
Il commento di LEON
La costruzione di quadrati magici di ordine 5 mediante un programma da far girare su personal computer presenta a mio giudizio due grosse difficoltà.
Tempo di elaborazione : se si utilizza un algoritmo di tipo "brute force", Il tempo per generare e controllare tutte le possibili matrici di ordine 5, dovrebbe essere dell’ordine di diversi anni.
Eliminazione di quadrati magici ripetuti : se si utilizza un altro tipo di algoritmo si deve poi controllare che i quadrati magici ottenuti siano tutti distinti.
Io ho utilizzato l’algoritmo del passo uniforme, che è una generalizzazione del metodo di De la Loubère. Mediante un apposito programma scritto in turbo pascal sono riuscito a costruire 52.992 quadrati magici distinti.
Si tratta di un valore ben lontano dalla soluzione conosciuta ma, grazie al metodo usato, posso affermare con certezza che i quadrati magici ottenuti sono tutti distinti.
Mi preme far notare che in rete ho trovato un programma che genera diverse centinaia di migliaia di quadrati magici del quinto ordine ma, ad un attento esame, ho verificato che molti di essi sono uguali.
Per questo motivo le soluzioni si devono controllare con molta attenzione.
Il file allegato contiene:
1) gioco37.pas = programma scritto in turbo pascal in cui è implementato l’algoritmo risolutivo
2) gioco37.exe = eseguibile di gioco37.pas, lanciabile direttamente da windows
3) fdelay.tpu = libreria per tp7, necessaria se si vuole far girare il programma dall’ambiente di sviluppo del tp7, su computer pentium. Essa va copiata nella cartella BP/UNITS. Non è necessaria su computer 486 o inferiore.
Il programma visualizza sullo schermo i quadrati magici.
Mediante il tasto F3 viene generato un file di testo (di nome magic.txt) contenente i 52.992 q.m. trovati.
Anche la soluzione di MATRIX , merita si essere letta. L’algoritmo che ha utilizzato dà 1472 quadrati magici distinti.
Leggiamo le sue note.
Uno dei metodi più antichi per determinare quadrati di ordine dispari è quello "De La Roubere", che non sto qui a descrivere (un link adatto http://mathforum.org/alejandre/magic.square/adler/adler.5x5math.html ). Questo metodo però genera pochi (solo 5) quadrati magici di ordine 5. Accanto a questo metodo ce ne sono molti altri, che però hanno lo stesso difetto: generano pochi quadrati magici.
Un metodo che genera 6624 quadrati magici di ordine 5 (52992 comprese le rotazioni e le riflessioni) è dovuto a Charles E. Jean (1988) – link : http://www.recreomath.qc.ca/art_magiques_ce.htm
L’approccio che ho seguito io fa riferimento invece al metodo del passo uniforme di Lehmer di cui do qui una breve descrizione :
Siano a, b, c, d, e, f degli interi, ed n un intero positivo (n=5 nel nostro caso). Nelle celle di una griglia nxn si pongono gli n2 i numeri 1, 2, 3, … n2 nelle celle di coordinate (xi ,yj ), dove :
xi=[a+c*i+e*INT(i/n)] MOD n +1
yi=[b+d*i+f*INT(i/n)] MOD n +1
E’ interessante notare che il metodo di De La Roubere è un caso particolare di questo, e si ottiene scegliendo opportunamente gli interi c, d, e ,f .
Per un approccio algoritmico al problema sono fondamentali sono i seguenti due teoremi :
Teorema: il metodo del passo uniforme di Lehmer riempie tutte le caselle del quadrato nxn se la quantità c*f-d*e è prima con n.
Teorema: se gli interi i=1,2, …n2 sono posti nelle celle di una griglia nxn con il metodo del passo uniforme di Lehmer, il quadrato è magico se e solo se i numeri c, d, e, f sono primi con n.
Sfruttando questi due teoremi, ho implementato un programma di calcolo che, a partire da opportuni valori di c, d, e, f determina 1742.
Ecco il programma eseguibile sotto Windows di Matrix
La soluzione di LUZZO (Trento)
Per costruire un quadrato magico di ordine dispari si può ricorrere alla regola di De la Loubrè. Questa regola può essere desunta dall’Enciclopedia della Matematica ed è la seguente. Si colloca il numero 1 nella casella centrale della riga superiore, si scrivono poi i numeri da 2 a n2 passando nella riga immediatamente superiore alla successiva casella a destra tenendo presente che:
· se si è arrivati ad una casella della riga superiore si passa alla riga inferiore come se questa fosse scritta al di sopra di quella segnando il numero della successiva colonna;
· arrivati all’ultima colonna a destra si passa alla prima colonna, come se questa fosse scritta dopo quella;
· se si arriva ad una casella già occupata o sull’ultima casella superiore, il numero si segna nella casella immediatamente al di sotto di quella in cui si trova l’ultimo numero scritto.
In questo caso si ha il quadrato magico fondamentale di ordine 5
| 17 | 24 | 1 | 8 | 15 |
| 23 | 5 | 7 | 14 | 16 |
| 4 | 6 | 13 | 20 | 22 |
| 10 | 12 | 19 | 21 | 3 |
| 11 | 18 | 25 | 2 | 9 |
dove la costante magica è 65. Da questo quadrato magico non è difficile accorgersi che tutti i suoi elementi sono formati dai numeri 1,2,3,4,5 e 0,5,10,15,20 per cui il quadrato precedente può essere così "scomposto":
| (15,2) | (20,4) | (0,1) | (5,3) | (10,5) |
| (20,3) | (0,5) | (5,2) | (10,4) | (15,1) |
| (0,4) | (5,1) | (10,3) | (15,5) | (20,2) |
| (5,5) | (10,2) | (15,4) | (20,1) | (0,3) |
| (10,1) | (15,3) | (20,5) | (0,2) | (5,4) |
Da qui si vede che se si fanno permutare i numeri 1,2,3,4,5 si hanno P1=5! permutazioni diverse; ne consegue che per preservare la proprietà di magicità del quadrato ai numeri 0,5,10,15,20 sono permesse solo P2=4! permutazioni diverse. Si hanno così P1*P2=4!*5!=2880 quadrati magici.
La soluzione di WONDERP
Ogni q.m. (quadrato magico) può essere ruotato originando 4 q.m. diversi.
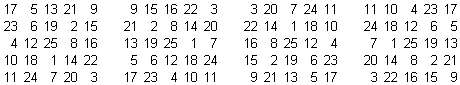
Posso scambiare 1a e 5a colonna, come indicato in figura o in contemporanea anche le righe

Quindi da ogni q.m. che trovo posso ricavarne 16. Si può notare che il centro è sempre costante, quindi se varia il centro varia anche il q.m.
D’ora in poi, non avendo usato programmi devo suddividere il problema in casi particolari.
Prendo in considerazione 5 serie:
A: 1 2 3 4 5;
B: 6 7 8 9 10;
C: 11 12 13 14 15;
D: 16 17 18 19 20;
E: 21 22 23 24 25;
Per iniziare parlo di q.m. che hanno su una diagonale la serie C:
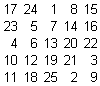
le altre serie sono disposte parallelamente alla serie C, osservando l’ultima riga l’ordine delle serie è C D E A B. Alla serie A posso sommare 5 e alla B sottrarre 5 in modo da "sostituirle":
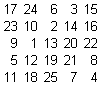
così l’ordine delle serie dell’ultima riga è ora C D E B A. Questo scambio posso farlo solo tra le serie A B D E ottenendo 4! =24 q.m. diversi. Non posso toccare C perché sulla diagonale. Ho trovato 7 tipi distinti (cioè non deducibili da rotazioni, scambi o "sostituzioni") di questo tipo di q.m.
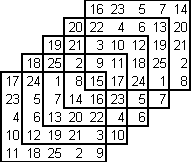
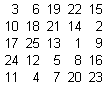
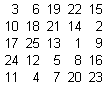
quindi da questo caso particolare posso ricavare 16*4!*7=2688 q.m. diversi. (attenzione! nelle regole suddette non ho messo nessuna simmetria perché deducibile da rotazioni (90°) e "sostituzioni", ad esempio A B D E con E D B A).
Un altro caso particolare si ottiene disponendo le serie non in obliquo ma "come si muove il cavallo" cosìcché su ogni riga, colonna e diagonale del q.m. ci sia uno e un solo numero per serie, graficamente si vede meglio:
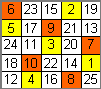
In questo caso le "sostituzioni" possono essere fatte tra tutte le serie, quindi 5! e non 4! diversi q.m. Ho trovato 6 tipi distinti di questi q.m.
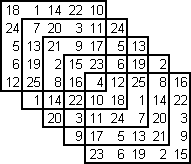
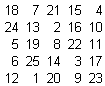
Quindi da questo caso particolare posso ricavare 16*5!*6=11520 q.m. diversi. (da notare che con le regole iniziali il centro non varia mai, quindi a centri diversi corrispondono q.m. diversi) con quest’ultimo sistema i centri sono 21 15 4 18 e 7 che divisi per 5 mi danno resto 1 0 4 3 e 2 quindi scambiando le serie riesco a mettere nel centro qualsiasi numero dall’1 al 25.
Ho altri casi che non sono riuscito a generalizzare e sono:
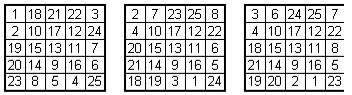
di questi non sono riuscito a trovare scambi, perciò oltre a rotazioni (4) e sostituzioni di righe e/o colonne posso anche fare la simmetria lungo una diagonale ottenendo così 32 diverse disposizioni per quadrato quindi 32*3=96
Totale:96+11520+2688=14304

eh, ma se si usa il computer è troppo facile!