|
|
Ruote
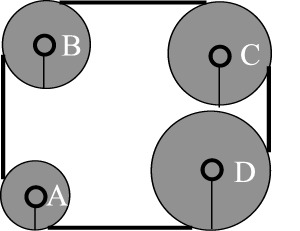
Quattro ruote A, B, C, D sono collegate tramite una cinghia e hanno rispettivamente raggi 14,15,16 e 18. Sono disposte come in figura in modo che il sistema sia libero di ruotare senza che la cinghia possa slittare. Dopo quanti giri della ruota A il sistema torna per la prima volta nella posizione iniziale? |
360 giri
La motivazione di Francesco Boano
Affinchè il sistema torni alla posizione iniziale le 4 ruote devono percorrere un "percorso" che sia multiplo di tutte e quattro.
Il percorso sarà quindi il minimo comune multiplo tra i "percorsi".
14 = 2 * 7
15 = 3 * 5
16 = 2^4
18 = 3^2 * 2
il percorso sarà quindi (2pi) ( 5 * 7 * 9 * 16)
e il numero di giri compiuti da A sarà (5 * 7 * 9 * 16) / 14 = 360
La motivazione di Aurelio Mascheroni
Ra, Rb, Rc, Rd -> raggi delle 4 ruote
x -> numero incognito di giri della ruota A
Dopo che A ruota di 1 giro, la cinghia trasla di 2*PIgreco*Ra e le altre ruote ruotano di un numero di giri dato rispettivamente da:
B -> 2*PIgreco*Ra /2*PIgreco*Rb = Ra/Rb
C -> Ra/Rc
D -> Ra/Rd,
poiché- in assenza di strisciamento- ciascuna ruota compie un numero di giri corrispondente al rapporto fra la lunghezza dell'arco di cui ha ruotato (eguale alla traslazione della cinghia) e quella dell'arco che corrisponde ad 1 giro completo.
Con i valori assegnati, dopo x giri di A le altre ruote ruotano di:
Nb= x*14/15
Nc= x*14/16= x*7/8
Nd= x*14/18= x*7/9
Affinché il sistema torni per la prima volta nella posizione iniziale, x deve rendere Na, Nb, Nc i più piccoli interi che soddisfano a tali equazioni.
Ciò porta alla ricerca del mcm dei denominatori delle 3 frazioni:
x = mcm (15, 8, 9) = 360
Per tale numero di giri di A si ottiene:
Nb= 336
Nc= 315
Nd= 280.