Se vi dico 2048, cosa vi viene in mente? Davvero? Dunque, anche voi l’avete già provato e magari sul vostro cellulare è installata l’App del gioco originale… Sia che siate riusciti a ottenere la famigerata “tile” da 2048, sia che ancora ci stiate provando, una domanda di certo ve la sarete posta almeno una volta: “Qual è il massimo punteggio ottenibile in questo gioco?”

Premesso che la tile più grande che può essere formata, con riferimento alla classica configurazione 4×4 del gioco, è $2^17=131072$ e che questo risulta possibile solo nel 10% delle “partite perfette giocate” (giacché nove volte su dieci comparirà un “2” e nei restanti casi un “4”), andiamo ad analizzare come vengono determinati i punteggi.

– Combinando due tile da 2 tra loro si segnano quattro punti, combinandone due da 4 se ne ottengono 12 e combinandone due da 8 si aggiungono 48 punti al punteggio totale. La regola è pertanto che, combinando fra loro due tile di valore $2^(k-1)$ (ed ottenendo una tile da $2^k$), si ricevono $(k-1)*2^k$ punti.

– Si inizia il gioco con 2 tile (entrambe da 2, ambedue da 4 o una da 2 e una da 4) sulla board e contano, per lo score, solo le tile che si combinano fra loro.

– Se non vengono commessi errori e si riesce ad arrivare fino in fondo al gioco, ma non si ha la fortuna di avere un 4 (anziché un 2) al momento opportuno, la partita termina senza riuscire a comporre la tile da 131072 e ci si ferma alla configurazione illustrata nel diagramma sottostante:

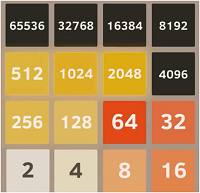 figura 1

Configurazione finale nel 90% delle partite perfette.

– Se invece capita di ottenere un 4 al posto del 2 della Figura 1, si può procedere combinando (a cascata) le tile da 4 per formarne una da 8, quelle da 8 per ottenerne un’altra da 16 e così via, fino alle due da 65536… in modo da formare la tile da 131072, la massima possibile in questo gioco.

Quale sarà il punteggio finale se apparirà un 2 e la partita perfetta terminerà con una tile massima da $2^16=65536$?

Come molto spesso accade in matematica, la risposta è… “dipende”! Dipende, perché non sappiamo quanti “quattro” sono apparsi sulla board… possiamo solo calcolare un valore massimo, uno minimo e uno atteso.

Sapendo che le tile combinate fra loro a questo punto del gioco sono state circa $131068/2.2=59576.364$, e che il massimo punteggio possibile (nell’ipotesi che siano comparsi solo “2” sulla scacchiera, senza mai un “4” – tranne quello che pone fine alla partita) è 4 + 16 + 48 + 128 + 320 + 768 + 1792 + 4096 + 9216 + 20480 + 45056 + 98304 + 212992 + 458752 + 983040 = 1835012, si può facilmente stimare il valore atteso (considerando una media di un “4” sulla board ogni nove “2” random): Valore atteso (massimo punteggio ottenibile, con partita perfetta, nel 90% dei casi) = $1835012-(59576.364/10)*4≈1811181.45$ → [1811180, 1811184]. Questo è lo score più probabile nel 90% delle partite perfette giocabili, con probabilità decrescenti man mano che ci si allontana da tale risultato.

In ogni caso, tutti i punteggi saranno compresi fra $1835012-131068/4*4=1703944$ (probabilità infinitesima, pari a $0.1^32766*0.9=9*10^(-32767)$ delle partite perfette giocabili) e il massimo di 1835012 punti.

Se invece, al momento propizio, appare un “4” e possiamo chiudere la catena, culminante nell’unione delle due tile da $2^16$, potremo procedere nel gioco.

Immaginando che questo raro evento possa ripetersi per 15 volte consecutive (una volta ogni milione di miliardi di partite perfette accadrà!), ci troveremo nella condizione seguente:

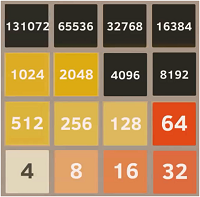figura 2

Miglior configurazione finale possibile nel gioco 2048 originale.

In questo caso, dopo 131052 mosse e 131053 tile effettive combinate (l’ultima, che sia un “2” o un “4”, è assolutamente ininfluente), il gioco si concluderà e il nostro punteggio più plausibile sarà prossimo a $3932160-((((262136-60)/2.2)/10)+15)*4≈3884449.82$ → [3884448, 3884452] (e comunque non inferiore a 3670024); tuttavia, con probabilità $0.1^15*0.9^(131053-15)≈1.0714*10^(-6009)%$, si otterrà il massimo possibile teorico di questo gioco: 3932100 punti!

Infatti, $∑_(n=3)^17 (n-1)*2^n -4*15=16*(2^17)+1835012-4-4*15=3932100$

(essendo impossibile ottenere i quattro punti derivanti dalla combinazione di due tile base [2]+[2] → [4] dopo che la tile massima da 131072 è stata formata e tale situazione si deve ripetere 15 volte in tutto prima di giungere alla configurazione illustrata in Figura 2).

Immaginando di effettuare (in media) una mossa al secondo, giocando in modo perfetto ed avendo una fortuna indicibile (una probabilità su $1.0714*10^6011$), dovremmo insistere per 131051 secondi prima di raggiungere il massimo punteggio teorico e per 131052 prima di terminare la partita… oltre un giorno e mezzo: 36 ore, 24 minuti e 12 secondi.

In generale, considerando un griglia nxn arbitraria (n≥2), il massimo punteggio realizzabile è così definito:

$∑_(n=3)^(n^2+1) (n-1)*2^n-(n^2-1)*4 = 2^((n^2+2) )*(n^2-1)-4*(n^2-1)=4*(n^2-1)*(2^(n^2 )-1)$

A gioco perfetto, per (n≥2), le chance di ottenere tale valore massimo sono appena

$0.1^((n^2-1))*0.9^((((2*2^((n^2+1))-8-(n^2-1)*4))/2)) = 0.1^((n^2-1))*0.9^((2^((n^2+1))-2n^2-2) )≈12.3457*0.1^(n^2 )*0.9^(2^(((n^2+1)-2n^2 ) ) ) $

n  max score teorico  probabilità di ottenerlo
 1 0  1 
 2  180  9.8477*10^(-5)
 3  16352  1.1468*10^(-54)
 4  3932100  1.0714*10^(-6011)
 5  3221225376  1.4736*10^(-3070755)
 6  9620726742900  infinitesima
 7  108086391056891712  infinitesima
 8  4648579506574807006980  infinitesima

Figura 3. Massimo score teoricamente ottenibile e relative probabilità per griglie di dimensione variabile.

Curiosità: il più basso punteggio realizzabile, sforzandosi di totalizzare il minimo di punti possibile ed essendo aiutati dalla (s)fortuna, è sempre zero (per qualsiasi valore di $n∈N{0}$).

Commenti

commenti