Un semplice giochino che vi farà scervellare. Con gli stessi pezzi è possibile comporre due triangoli, uno più grande dell’altro, come mai?
Disegna su un foglio i seguenti pezzi di triangolo
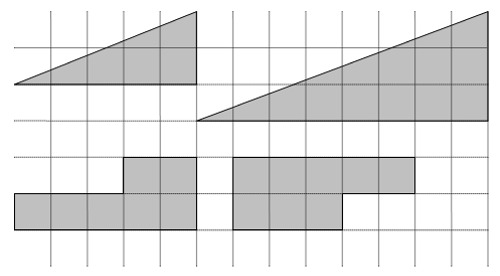
scarica da qui il file pdf da stampare
Ricomponi il triangolo nel seguente modo
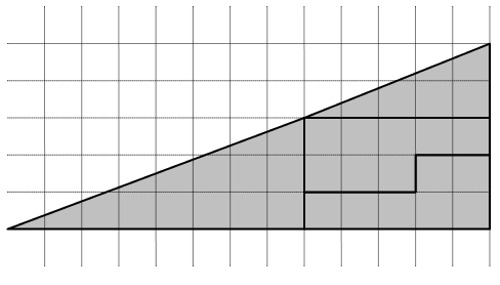
Ricomponi il triangolo in quest’altro modo
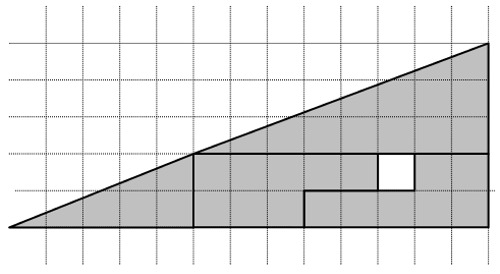
Come mai questo triangolo pur avendo base 13 come il precedente e altezza 5 come il precedente, ha una superficie maggiore in quanto ha il quadratino bianco in più?

Ma si vede! Se si guarda attentamente l’ipotenusa dei due triangoli si vede che è diversa, il primo triangolo non fa lo stesso percorso sulla griglia del secondo, sembra addirittura lievemente curva.
Sembrano uguali ma hanno pendenza diversa.
Infatti riproducendo le figure in Autocad e facendo la sovrapposizione dei due triangoli, si nota la diversa pendenza e facendo la differenza delle due aree si ottiene quella del quadratino.
non riesco a capire il gioco e poi è noioso non sò come si fa a guardare
è facilissimo, appena l’ ho visto mi sono accorta subito che in verità quelli non sono un triangoli. non ci vuole una grandissima intelligenza, ho 7 anni
Wow! Pensavo che la matematica fosse più facile! Per quanto riguarda l’articolo, cosa c’è di strano? Non è certo l’unica meraviglia di questo mondo! Si può fare! Non c’è niente di strano!
ma va? semplice illusione ottica
le 2 aree non possono essere matematicamente uguali perchè il primo triangolo e’composto da un quadratino in meno
Un paradosso geometrico?
Eppure la somma delle aree dei poligono che formano i triangoli e’ la stessa,come e’ la stessa l’area dei triangoli. Mi piacerebbe sapere!
Il primo è un quadrilatero e non un triamgolo. saluti
hey maru questi calcoli di geometria tienili per te,
è UN TRIANGOLO!!!
non sono uguali, con il teorema di pitagora, la somma dei quadrati dei cateti dei due triangolini deve essere uguale alla somma dei quadrati dei cateti del triangolo grande.
secondo triangolo 25 più 4 29 primo triangolino,
64 più 9 secondo triangolino 73 ma il triangolo grande è 169 più 25 194 che diverso dalla somma delle ipotenuse piccole che è 102!!!!!!!!
non è un triangolo!!!!!!!!!
il gioco o, per meglio dire, il trucco è strabiliante… ore lo farò vedere a mia sorella…
é un gioco fantastico. l’ho fatto e mi ha quasi emozionato… complimenti
è molto semplice la soluzione basta osservare bene come si spostano la due figure dentro hai triangoli
le figure ottenute unendo i pezzi sembrano triangoli ma in realtà non lo sono xkè non sono simili i triangolini che si scambiano di posizione essendo differenti i rapporti tra i loro cateti infatti 2/5 è diverso da 3/8.è quindi inutile applicare la formula dell’area dei triangoli a poligoni che non sono triangoli.
i due triangoli non hanno la stessa pendenza. lo si nota novrapponendoli, e la differenza tra i due totale è proprio quel quadrato che manca. conplimenti per il sito
10 anni risolto
é davvero un problema interessante, lo voglio fare al mio prof di mate!
Non ho voglia di scervellarmi… u.u
gli angoli acuti dei tringoli non sono uguali pertanto le figure non formano perfettamente un triangolo.
inoltre l’area dei quattro pezzi è 32 mentre quella dello pseudo-triangolo di base 13 e altezza 5 è 32,5
cavolata
semplicemente si deve notare che i due poligoni di quattro lati sono diversi e quindi disposti in un senso vanno come ad incastro invece invertiti non coincidono più
wow…………………. è davvero un mistero… ke però scoprirò molto presto…. mi piace moltisssssssssssimo … è stupendo..oooooooooooooooooooooooooom è meravigliosoooooooooooooooooooooooooooooooooo… lo farò fare a tutti i miei amici più cari … vedremo se riuscianno a farlo … aperiamo di si……… bello davvero
è bellissimissimissimissimissimissimissimo
l’area del quadratino che scompare in pratica è spalmata lungo tutta ipotenusa del triangolone…capirlo non è facile o almeno per me non è stato facile…ma qui sembra che sono tutti dei geni…
è ‘na cavolata io ci avevo 9 in mattematica
nn ci ho capito molto…
I due triangoli non sono simili:uno ha tangente 3/8 e l’altro 2/5(per l’angolo acuto). Quindi le due figure non sono triangoli.
lo avevo già visto da qualche parte…
ma come è possibile??????????????????????????????????
ha scambiato il triangolo grande cn quello piccolo! avete capito? (credo) =):-)xD
l’ipotenusa di ogni triangolo non è una retta ma sono due segmenti, perche non sono dritte
è vero! le due ipotenuse dei trangoli piccoli non sono adiacenti! in conclusione quello è un quadrilatero convinto di essere un triangolo!
sinceramente nn ho capito niente? sarà ke in matematica ho solo nove e nelle altre materie 10. A ME GEOMETRIA NN PIACE… qualcuno me lo potrebbe spiegare, please
clrscr ,nn è un trucchetto di ottica !!!!!se lo sarebbe me lo spiegheresti???!! vediamo se ce la fai!…
AS ,GUARDA CHE NN CENTRA AFFATTO L’ INCLINAZIONE !!!!!..NN CENTRA L’IPOTENUSA!.QUELLO CHE HAI DETTO TE è ASSOLUTAMENTE SBAGLIATO!!.SEGUENDO QUELLO CHE HAI DETTO TU ,L’AREA COME FA AD ESSERE UGUALE IN ENTRAMBI TRIANGOLI !!
juniOr gyarda che nn è un’illusione ottica !!!!!!!!! come ve lo devo spiegare ,anche giuspeppe crede quello che hai detto ,ma nn è assolutamente vero ????? se vuoi chiedilo alla mia profesoressa Trapani..nn sai come è se parli durante la sua lezione ti massacra!
oO-MaRs-Oo,la posizione delle figure all’ interno del triangoli ,ok,hanno cambiato posizione , ma l’ area dei due triangoli è la stessa ,quindi nn centra la posizione delle figure !è sbagliato quello che hai detto !!!!!!! è un’assurdita esagerata !
…cioè si vede dopve sta il trucco…(nel caso nn lo vedessi t consiglio d prendere un paio di occhiali!)
ha ragione chi dice che l’ipotenusa sono 2 segmenti consecutivi e non 1 solo anche perchè se calcolate l’area di un trianglo 13×5 vi viene 32,5 e se fate la somma delle aree dei 4 pezzi vi viene 32
fa schifo questo gioco
Questo gioco è molto carino!
Questo gioco è troppo bello
nn è molto simpatico ma è un gioco per i minori di 6 anni…secondo me dovrebbero farne uno un pò più complicato per quelli della nostra età…comunque è tvb
ma è proprio na cretinata…nn capisco come ha fatto ad inventarlo…mmmha…vi amo!!!!!!!!!!!!!muah
Bello ^_^
e facilissimo!
nn ho cpt niente!!!
molto semplice da capire!
ma ke cretinata
MA NON CAPITE?!?!?!?!?!?? I DUE TRIANGOLI SONO UGUALI, MA LE 2 FIGURE ALL’INTERNO DEL TRIANGOLO HANNO CAMBIATO POSIZIONE, IN MODO DA CREARE UN BUCHETTO VUOTO!!!!!!!!!!!!!!!!!!!!!!!!!!
e 1 deficienza!!!!
e propio 1 scemenza!!!!!
Il secondo triangolo ha la superficie maggiore al primo, semplicemente, perché il secondo triangolo non è un triangolo.
il gioco ora che lo ho capito è facile… ma x arrivarci mi sono fatta aiutare…. xD xD qualche gioco decente ce la facciamo a metterlo???? =)
fa schifoooooooooooo
carino il gioco poco chiare le istruzioni
non riesco proprio a capire questo gioco!
uffaaaaaa!!!!!!!!!!!!!!!!
aiutatemi!
per favore, me lo spiegate? ho contato anche i quadretti delle figure che li compongono, non riesco a capire come sbuca fuori quello spazio bianco!
sullo stesso principio di questo paradosso su “matematica dilettevole e curiosa” di Italo Gherzi, simpatico libro che consiglio, si scompone una scacchiera 8×8 in quattro figure, due triangoli e due trapezi, per poi ricomporre un rettangolo 5×13 giungendo a (assurda) conclusione che 64=65!
L’errore e’ il medesimo: 5/13 NON corrisponde a 3/8.
Piu’ prossime le frazioni piu’ l’errore sara’ nascosto (all’occhio, non alla logica che rimane la medesima) come con 7/24 e 9/31. Saluti, TJM.
le ipotenuse sono delle linee spezzate nei punti di unione dei triangoli rettangoli piccoli
è un effetto ottico . variano le inclinazioni delle ipotenuse.
non c’è nessuna illusione ottica le due figure sono identiche (provate a farlo su carta se non ci credete)
la soluzione è banale ma comunque matematica…
…Dovrebbe essere un gioco di matemagica???
Dipende dalla matematica che stai considerando… anche 2+2=5 può essere vero :-)
Giochino VECCHIO, lo faceva gia Lewis Carrol nella sua ‘Matemagica’ …
nn ci ho capito nulla…!!!!!
è troppo difficile scrivere un commento su questo sito!
le figure sono diverse, è un illusione ottica
Hanno due inclinazioni diverse.. l’ipotenusa del secondo non è un segmento dritto
Questo è più un trucchetto di ottica che un giochetto matematico…ahaha!!!!
Il trucco è nel rettangolo all’interno del triangolo: nella prima figura il rettangolo ha area 5*3, nella seconda 8*2 – 1*1
Do un suggerimento a chi vuole risolverlo: 3/8 e 2/5 non sono lo stesso numero… :-)
In realtà il triangolo non sarebbe ***. Infatti i 2 triangolini ***. Per questo le inclinazioni delle 2 ipotenuse ***.
*** = censura di admin