In questo articolo si richiama il concetto di “modello matematico” in contrapposizione a quello di “legge matematica di natura”, si fa cenno alla “System Dynamics”, modellistica di simulazione deterministica ideata lo scorso secolo dall’Ingegnere Statunitense J.W. Forrester , si introducono poi i modelli epidemiologi SIR (Suscettibili, Infetti, Rimossi) che portano alla formulazione di un sistema di tre equazioni differenziali in tre incognite. Il modello SIR viene poi tradotto in Equazioni di Livello e di Flusso proprie della dinamica dei sistemi. Infine Il modello di Simulazione, basato sulla Dinamica dei Sistemi, viene applicato ad un semplice esempio numerico.
Modelli matematici
Il paragrafo è liberamente tratto da uno scritto del Prof. Claudio Bartocci citato in bibliografia.
Il concetto di modello matematico si precisa, nella sua accezione moderna, verso la fine dell”800, nell’opera profondamente innovatrice di Henri Poincaré (1854-1912), geniale matematico, fisico e filosofo. Poincaré è stato forse il primo che, nei suoi scritti di riflessione sulla scienza, ha scardinato l’impianto epistemologico di Galileo, di Keplero e di Newton asserendo esplicitamente la possibilità di descrizioni matematiche non univoche dei fenomeni fisici e confutando ogni pretesa di universalità (ad uno stesso fenomeno fisico possono essere associati diversi modelli più o meno efficaci ed utili).
Un modello matematico non aspira a cogliere l’essenza ultima dei fenomeni ma si limita a fornire un’analogia formale che permetta di rappresentarne alcuni aspetti: un modello non ci dice come funzionano le cose ma soltanto che le cose funzionano “come se”.
Il primo ad aver formulato in maniera esplicita la nozione di modello in tutta la sua generalità è stato John von Neumann (1903-1957), uno dei più versatili scienziati del ‘900: logico matematico (ha lavorato con Hilbert all’impostazione assiomatica della matematica) e studioso dei fondamenti della Meccanica quantistica, creatore (insieme con Oskar Morgenstern) della Teoria dei Giochi, pioniere della Computer Science e della Teoria degli Automi. Ecco le parole di von Neumann: “per modello si intende un costrutto matematico che, con l’aggiunta di certe interpretazioni verbali, descrive dei fenomeni osservati. La giustificazione di un costrutto matematico del genere è soltanto e precisamente che ci si aspetta che funzioni – cioè che descriva correttamente i fenomeni di un’area ragionevolmente ampia. Inoltre, esso deve soddisfare certi criteri estetici – cioè, rispetto alla quantità di informazione che fornisce, deve essere piuttosto semplice”. In quest’ultimo passo si ravvisa un richiamo al rasoio di Occam (XIV secolo d.c.): “frustra fit per plura quod potest fieri per pauciora” (è futile fare con più mezzi quello che si può fare con meno). Ovvero: “ Entia non sunt multiplicanda sine necessitate” (Non moltiplicare gli enti più del necessario).
Riassumendo, i modelli matematici hanno le seguenti caratteristiche fondamentali: sono locali, descrittivi, non unici, parziali, non normativi né prescrittivi. Non sono altro che “frammenti di matematica incollati su frammenti di realtà” (come scritto da G. Israel nel libro “La visione matematica della realtà”, Laterza, Roma-Bari, 1997), con zone di sovrapposizione o – talvolta – addirittura di incompatibilità. Il fatto di accettarli come “empiricamente adeguati” (per usare un’espressione di van Fraassen, filosofo olandese nato nel 1941) non implica nessuna asserzione ontologica riguardo ai fenomeni cui si applicano. Per la stessa ragione, non dobbiamo stupirci se, a volte, le cose non funzionano troppo bene, se le approssimazioni risultano grossolane, se gli assunti si rivelano ingiustificate a un esame più approfondito. Il metodo fondamentale della modellistica matematica è l’analogia matematica con il fenomeno oggetto di studio.
La Fisica teorica – tanto la Meccanica newtoniana, quanto la Relatività e la Meccanica quantistica – è l’ambito scientifico in cui l’interpretazione pitagorico-platonica è stata senza dubbio predominante (da Galileo e Newton fino a Einstein e Dirac). E possiamo dire che sia predominante ancor oggi: la teoria delle stringhe si fonda sul presupposto che esista una “teoria del tutto” in grado di spiegare tutta la realtà fisica, dall’infinitamente piccolo all’infinitamente grande. D’altra parte, in settori disciplinari quali la Biologia, le Scienze Sociali o le Scienze Economiche, la modellistica matematica si è dimostrata, più modestamente, come l’unica strada percorribile per affrontare, anche se con approssimazioni, la complessità dei fenomeni da studiare.
Suscettibili (S), Infetti (I) e Rimossi (R)
Il paragrafo segue l’impostazione data dai Prof. Pontrelli e De Lillo nel loro scritto: “Modelli matematici: i tanti volti della realtà” e dalla voce di Wikipedia “Modelli matematici in epidemiologia”.
I modelli SIR sono importanti in Epidemiologia, in particolare sono stati applicati con un certo successo alla descrizione della evoluzione di malattie come il morbillo, la parotite e la rosolia:
• Ogni individuo può essere infettato da un agente patogeno solo una volta e poi diventa immune o muore.
• La popolazione è costante. Le morti dovute alla malattia sono incluse nel gruppo Rimossi. Le nascite e le morti per altre ragioni non sono prese in considerazione.
• Gli infetti sono immediatamente contagiosi.
• Un soggetto Suscettibile diventa infetto con tasso di contagio che si assume costante.
• Il tasso di contagio o velocità di trasmissione si assume uguale a “b”.
• Gli Infetti diventano Rimossi con un tasso costante uguale a “g”.
Sia:
• S numero degli individui suscettibili di contrarre la malattia (DS/dt, la variazione),
• I numero degli infetti (DI/dt, la variazione nel tempo)
• R numero dei rimossi, morti e guariti (dR/dt, la variazione nel tempo)
• So, Io, Ro le condizioni iniziali.
• b il tasso di contagio
• g il tasso di rimozione.
Con queste premesse il Sistema di 3 equazioni differenziali del primo ordine nelle tre incognite S, I, R, è:
dS/dt = -b*I*S
dI/dt = b*I*S – g*I
dR/dt = g*I
Il modello si chiama compartimentale in quanto appare composto da tre compartimenti (o serbatoi volendo seguire l’analogia idraulica) in cui la somma del liquido contenuto totale è sempre costante. Infatti:
dS/dt + dI/dt + dR/dt = -b*I*S + b*I*S – g*I + g*I = 0
Ovvero Sk + Ik + Rk = Costante.
Se So > g/b gli infetti (I) prima cresceranno, avranno un massimo e poi decresceranno sino ad annullarsi.
La System Dynamics (S.D.) di Forrester
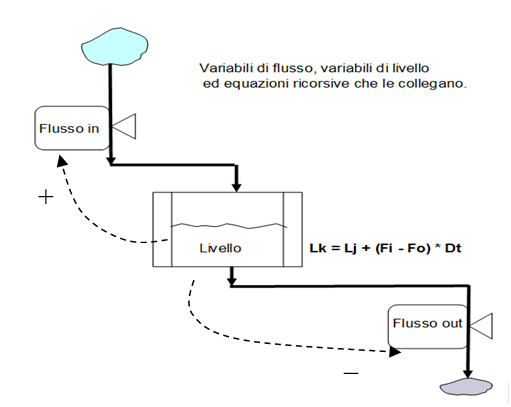Lo strumento quantitativo ideato da Forrester per modellare i problemi delle organizzazioni è eccezionale per la sua semplicità: variabili di flusso (derivate o valori di periodo), e variabili di livello (integrali o valori cumulati). La metafora idraulica (vedi figura) è tra le migliori per comprendere la Dinamica dei Sistemi (S.D., System Dynamics). In un progetto, ad esempio, le ore spese periodo per periodo, cioè l’istogramma di carico, sono rappresentate dalla portata del rubinetto (il flusso) che può variare da un periodo all’altro. L’avanzamento fisico progressivo (o cumulato), cioè la curva ad “S”, è rappresentato dal livello del recipiente che, dopo un certo tempo (la durata del progetto), grazie al flusso periodico delle ore lavorate, raggiunge il 100% (recipiente colmo e progetto completato).
Avremo dunque le variabili di flusso che influenzano i livelli (tratto continuo) e le variabili di livello che influenzano i flussi attraverso interazioni informative (tratteggiate). In figura il segno “+” rappresenta un circuito di retroazione (feed-back) positivo, mentre il segno (-) un circuito di retroazione negativa. Con le nuvolette si rappresentano variabili di livello esterne al sistema in studio, che non vengono quindi prese in considerazione.
Applicazione della SD ai modelli SIR
Vediamo ora come le tre equazioni differenziali del modello SIR possono essere trasformate in tre equazioni di Livello e tre equazioni di Flusso della S.D. Come passo della simulazione assumiamo Dt = 1 giorno, che quindi non compare nelle equazioni:
Livelli:
Sk+1 = Sk + Fs
Ik+1 = Ik + Fi – Fr
Rk+1 = Rk +Fr
Flussi:
Fs = -b*Ik*Sk
Fi = b*Ik*Sk
Fr = g*Ik
Un esempio numerico
L’esempio numerico è tratto dal citato articolo in bibliografia di Wikipedia
https://upload.wikimedia.org/wikipedia/commons/thumb/b/bd/SIR-Modell.svg/1024px-SIR-Modell.svg.png
Condizioni Iniziali:
So = 997
Io = 3
Ro = 0
Tassi:
b = 0.04%
g = 4.00%
g/b = 100.00
Il modello è stato esteso a tre mesi, più esattamente 90 giorni. Di seguito si riportano i risultati ottenuti:
| k | Sk | Ik | Rk | Fs | Fi | Fr |
| 0 | 997.000 | 3.000 | 0.000 | -1.196 | 1.196 | 0.120 |
| 1 | 995.804 | 4.076 | 0.120 | -1.624 | 1.624 | 0.163 |
| 2 | 994.180 | 5.537 | 0.283 | -2.202 | 2.202 | 0.221 |
| 3 | 991.978 | 7.518 | 0.505 | -2.983 | 2.983 | 0.301 |
| 4 | 988.995 | 10.200 | 0.805 | -4.035 | 4.035 | 0.408 |
| 5 | 984.960 | 13.827 | 1.213 | -5.447 | 5.447 | 0.553 |
| 6 | 979.513 | 18.721 | 1.766 | -7.335 | 7.335 | 0.749 |
| 7 | 972.178 | 25.307 | 2.515 | -9.841 | 9.841 | 1.012 |
| 8 | 962.336 | 34.136 | 3.527 | -13.140 | 13.140 | 1.365 |
| 9 | 949.196 | 45.911 | 4.893 | -17.431 | 17.431 | 1.836 |
| 10 | 931.765 | 61.506 | 6.729 | -22.924 | 22.924 | 2.460 |
| 11 | 908.841 | 81.969 | 9.190 | -29.799 | 29.799 | 3.279 |
| 12 | 879.042 | 108.490 | 12.468 | -38.147 | 38.147 | 4.340 |
| 13 | 840.895 | 142.297 | 16.808 | -47.863 | 47.863 | 5.692 |
| 14 | 793.033 | 184.468 | 22.500 | -58.516 | 58.516 | 7.379 |
| 15 | 734.517 | 235.604 | 29.879 | -69.222 | 69.222 | 9.424 |
| 16 | 665.295 | 295.402 | 39.303 | -78.612 | 78.612 | 11.816 |
| 17 | 586.683 | 362.198 | 51.119 | -84.998 | 84.998 | 14.488 |
| 18 | 501.685 | 432.708 | 65.607 | -86.833 | 86.833 | 17.308 |
| 19 | 414.852 | 502.233 | 82.915 | -83.341 | 83.341 | 20.089 |
| 20 | 331.511 | 565.485 | 103.004 | -74.986 | 74.986 | 22.619 |
| 21 | 256.525 | 617.851 | 125.624 | -63.398 | 63.398 | 24.714 |
| 22 | 193.127 | 656.535 | 150.338 | -50.718 | 50.718 | 26.261 |
| 23 | 142.409 | 680.991 | 176.599 | -38.792 | 38.792 | 27.240 |
| 24 | 103.617 | 692.544 | 203.839 | -28.704 | 28.704 | 27.702 |
| 25 | 74.914 | 693.546 | 231.541 | -20.782 | 20.782 | 27.742 |
| 26 | 54.131 | 686.586 | 259.282 | -14.866 | 14.866 | 27.463 |
| 27 | 39.265 | 673.989 | 286.746 | -10.586 | 10.586 | 26.960 |
| 28 | 28.679 | 657.615 | 313.705 | -7.544 | 7.544 | 26.305 |
| 29 | 21.135 | 638.855 | 340.010 | -5.401 | 5.401 | 25.554 |
| 30 | 15.734 | 618.701 | 365.564 | -3.894 | 3.894 | 24.748 |
| 31 | 11.840 | 597.847 | 390.312 | -2.832 | 2.832 | 23.914 |
| 32 | 9.009 | 576.765 | 414.226 | -2.078 | 2.078 | 23.071 |
| 33 | 6.930 | 555.773 | 437.297 | -1.541 | 1.541 | 22.231 |
| 34 | 5.390 | 535.082 | 459.528 | -1.154 | 1.154 | 21.403 |
| 35 | 4.236 | 514.833 | 480.931 | -0.872 | 0.872 | 20.593 |
| 36 | 3.364 | 495.112 | 501.524 | -0.666 | 0.666 | 19.804 |
| 37 | 2.698 | 475.974 | 521.329 | -0.514 | 0.514 | 19.039 |
| 38 | 2.184 | 457.448 | 540.368 | -0.400 | 0.400 | 18.298 |
| 39 | 1.784 | 439.550 | 558.666 | -0.314 | 0.314 | 17.582 |
| 40 | 1.471 | 422.282 | 576.248 | -0.248 | 0.248 | 16.891 |
| 41 | 1.222 | 405.639 | 593.139 | -0.198 | 0.198 | 16.226 |
| 42 | 1.024 | 389.612 | 609.364 | -0.160 | 0.160 | 15.584 |
| 43 | 0.864 | 374.187 | 624.949 | -0.129 | 0.129 | 14.967 |
| 44 | 0.735 | 359.349 | 639.916 | -0.106 | 0.106 | 14.374 |
| 45 | 0.629 | 345.080 | 654.290 | -0.087 | 0.087 | 13.803 |
| 46 | 0.542 | 331.364 | 668.094 | -0.072 | 0.072 | 13.255 |
| 47 | 0.471 | 318.181 | 681.348 | -0.060 | 0.060 | 12.727 |
| 48 | 0.411 | 305.514 | 694.075 | -0.050 | 0.050 | 12.221 |
| 49 | 0.360 | 293.344 | 706.296 | -0.042 | 0.042 | 11.734 |
| 50 | 0.318 | 281.652 | 718.030 | -0.036 | 0.036 | 11.266 |
| 51 | 0.282 | 270.422 | 729.296 | -0.031 | 0.031 | 10.817 |
| 52 | 0.252 | 259.636 | 740.113 | -0.026 | 0.026 | 10.385 |
| 53 | 0.226 | 249.276 | 750.498 | -0.022 | 0.022 | 9.971 |
| 54 | 0.203 | 239.328 | 760.469 | -0.019 | 0.019 | 9.573 |
| 55 | 0.184 | 229.774 | 770.042 | -0.017 | 0.017 | 9.191 |
| 56 | 0.167 | 220.600 | 779.233 | -0.015 | 0.015 | 8.824 |
| 57 | 0.152 | 211.791 | 788.057 | -0.013 | 0.013 | 8.472 |
| 58 | 0.139 | 203.332 | 796.529 | -0.011 | 0.011 | 8.133 |
| 59 | 0.128 | 195.210 | 804.662 | -0.010 | 0.010 | 7.808 |
| 60 | 0.118 | 187.412 | 812.471 | -0.009 | 0.009 | 7.496 |
| 61 | 0.109 | 179.924 | 819.967 | -0.008 | 0.008 | 7.197 |
| 62 | 0.101 | 172.735 | 827.164 | -0.007 | 0.007 | 6.909 |
| 63 | 0.094 | 165.832 | 834.073 | -0.006 | 0.006 | 6.633 |
| 64 | 0.088 | 159.205 | 840.707 | -0.006 | 0.006 | 6.368 |
| 65 | 0.082 | 152.843 | 847.075 | -0.005 | 0.005 | 6.114 |
| 66 | 0.077 | 146.734 | 853.189 | -0.005 | 0.005 | 5.869 |
| 67 | 0.073 | 140.869 | 859.058 | -0.004 | 0.004 | 5.635 |
| 68 | 0.069 | 135.239 | 864.693 | -0.004 | 0.004 | 5.410 |
| 69 | 0.065 | 129.833 | 870.102 | -0.003 | 0.003 | 5.193 |
| 70 | 0.062 | 124.643 | 875.296 | -0.003 | 0.003 | 4.986 |
| 71 | 0.059 | 119.660 | 880.281 | -0.003 | 0.003 | 4.786 |
| 72 | 0.056 | 114.877 | 885.068 | -0.003 | 0.003 | 4.595 |
| 73 | 0.053 | 110.284 | 889.663 | -0.002 | 0.002 | 4.411 |
| 74 | 0.051 | 105.875 | 894.074 | -0.002 | 0.002 | 4.235 |
| 75 | 0.049 | 101.642 | 898.309 | -0.002 | 0.002 | 4.066 |
| 76 | 0.047 | 97.579 | 902.375 | -0.002 | 0.002 | 3.903 |
| 77 | 0.045 | 93.677 | 906.278 | -0.002 | 0.002 | 3.747 |
| 78 | 0.043 | 89.932 | 910.025 | -0.002 | 0.002 | 3.597 |
| 79 | 0.042 | 86.336 | 913.622 | -0.001 | 0.001 | 3.453 |
| 80 | 0.040 | 82.884 | 917.076 | -0.001 | 0.001 | 3.315 |
| 81 | 0.039 | 79.570 | 920.391 | -0.001 | 0.001 | 3.183 |
| 82 | 0.038 | 76.388 | 923.574 | -0.001 | 0.001 | 3.056 |
| 83 | 0.036 | 73.334 | 926.629 | -0.001 | 0.001 | 2.933 |
| 84 | 0.035 | 70.402 | 929.563 | -0.001 | 0.001 | 2.816 |
| 85 | 0.034 | 67.587 | 932.379 | -0.001 | 0.001 | 2.703 |
| 86 | 0.033 | 64.884 | 935.082 | -0.001 | 0.001 | 2.595 |
| 87 | 0.033 | 62.290 | 937.678 | -0.001 | 0.001 | 2.492 |
| 88 | 0.032 | 59.799 | 940.169 | -0.001 | 0.001 | 2.392 |
| 89 | 0.031 | 57.408 | 942.561 | -0.001 | 0.001 | 2.296 |
| 90 | 0.030 | 55.112 | 944.858 | -0.001 | 0.001 | 2.204 |
Il giorno 18 la curva dei Suscettibili (S), che è decrescente, ha un flesso, passa da convessità verso l’alto a convessità verso il basso, continua a decrescere, ma un po’ meno (vedi il valore di Fs). Inoltre tra il giorno 18 e il 19 la curva S incrocia la curva I.
Il giorno 25 si ha il Picco degli Infetti (I). Infatti la sua derivata numerica (Ik+1 – Ik)/1 = Fs + Fr, si annulla. Nello stesso giorno la curva dei Rimossi (R) ha un flesso (massimo di Fr).
A parole il modello SIR può essere così descritto: esiste una popolazione (S) sana ma Suscettibile di ammalarsi nel tempo. Con il trascorrere del tempo S decresce perché le persone iniziano ad infettarsi. Gli Infetti cominciano a guarire o a morire (R). Il numero degli Infetti (I) raggiunge il Picco massimo e poi inizia a decrescere tendendo asintoticamente a zero. Alla fine tutta la popolazione S sarà guarita o morta, cioè Rimossa (R).
Nel foglio Excel allegato è riportato il modello matematico.
Il lettore interessato può effettuare le sue simulazioni variando le condizioni iniziali, il tasso di contagio e di rimozione ed il numero di giorni considerato.
Bibliografia e Sitografia:
Claudio Bartocci: Modelli Matematici
https://sites.google.com/view/tulamblog/home/cultura/ilmondoematematico
Roberto Chiappi: Previsioni, Filosofia e Matematica
Roberto Chiappi: Sistemi matematici discreti, mappe di ricorrenza
Roberto Chiappi: La Dinamica dei Sistemi (J.W. Forrester)
Roberto Chiappi: Dinamica dei Sistemi
Roberto Chiappi: Modello Idraulico di una Epidemia
Wikipedia: Modelli matematici in Epidemiologia
https://it.wikipedia.org/wiki/Modelli_matematici_in_epidemiologia
Sir Model Illustrated Using System Dynamics
Pontrelli, Di Lillo: Modelli Matematici, i tanti volti della realtà
https://www.iac.cnr.it/~pontrell/pub/model.pdf
Pandemic Covid explained with the help of System Dynamics
https://www.esb-business-school.de/en/school/news/news/2020/corona-with-the-sir-model/