Il calorimetro
Il calorimetro è uno strumento molto utile che permette di determinare, a partire da quello dell’acqua, il calore specifico di determinate sostanze.
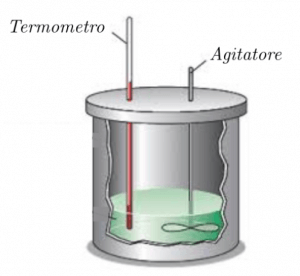
Questo strumento è costituito da un recipiente piuttosto leggero, che non assorba una gran quantità di calore, e isolato termicamente. All’interno del recipiente, riempito con dell’acqua, è posto un termometro che servirà per valutare l’aumento di temperatura di questa in seguito all’aggiunta della nostra sostanza.
Ipotizziamo di voler determinare il calore specifico di una barretta di un certo metallo.
Per prima cosa, dobbiamo conoscere la quantità d’acqua che si sta utilizzando e la sua temperatura iniziale; successivamente possiamo immergere la barretta (di cui conosciamo la massa e la temperatura iniziale) all’interno del calorimetro.
Come sappiamo, quando due corpi di diversa temperatura vengono a contatto, vi è un passaggio di calore dal corpo più caldo a quello più freddo, fino a che entrambi non raggiungono la stessa temperatura.
Anche in questo caso, quindi, indipendentemente da quale dei due sia il corpo più caldo, dopo un certo periodo di tempo, l’acqua del calorimetro e la barretta metallica avranno raggiunto la stessa temperatura, che è una temperatura di equilibrio.
Ipotizziamo che la barretta metallica sia l’oggetto più caldo: in questo caso, la barretta cederà parte del suo calore interno all’acqua, e la quantità di calore ceduto è pari a:
$Q_m = c_m * m_m * (T_e – T_m) $
dove $c_m$, $m_m$, $T_m$ rappresentano, rispettivamente, il calore specifico del metallo, la massa della barretta e la sua temperatura iniziale.
Allo stesso modo, possiamo calcolare quanto calore viene assorbito dall’acqua:
$ Q_a = c_a * m_a * (T_e – T_a) $
dove, anche qui, $c_a$ , $m_a$ , $T_a$ rappresentano, rispettivamente, il calore specifico dell’acqua, la sua massa e la sua temperatura iniziale.
Dato che il calorimetro è isolato termicamente, esso non può scambiare calore con l’ambiente esterno; ciò significa che, per la conservazione dell’energia, il calore che viene ceduto dal metallo deve essere uguale a quello che viene acquistato dall’acqua.
Di conseguenza la somma delle quantità di calore scambiate è uguale a zero:
$Q_m + Q_a = 0$
Infatti, dal momento che la temperatura di equilibrio sarà maggiore della temperatura iniziale dell’acqua, il calore assorbito dall’acqua avrà segno positivo; al contrario, la temperatura di equilibrio è minore di quella iniziale del metallo, e quindi il calore ceduto dalla barretta ha segno meno.
Sostituendo a questa uguaglianza le espressioni trovate precedentemente per il calore, possiamo ricavare il calore specifico della barretta di metallo:
$ c_m * m_m * (T_e – T_m) = – c_a * m_a * (T_e – T_a) to $
$ c_m = – frac( c_a * m_a * (T_e – T_a))(m_m * (T_e – T_m))$
In alcuni casi, invece, sono noti entrambi i calori specifici delle sostanze che costituiscono la soluzione, ed è necessario calcolare la temperatura di equilibrio che viene raggiunta dopo il loro mescolamento; possiamo utilizzare, quindi, l’equazione precedente per risalire alla temperatura di equilibrio $T_e$:
$ c_m * m_m * (T_e – T_m) + c_a * m_a * (T_e – T_a) = 0 to $
$ T_e = frac( c_a * m_a * T_a + c_m * m_m * T_m)(c_a * m_a + c_m * m_m)$
Esercizio
Consideriamo un calorimetro contenente una quantità d’acqua di 0,50 kg alla temperatura di 15°C, e immergiamo in esso in dischetto di piombo di massa 0,30 kg che, inizialmente, si trova alla temperatura di 90°C. Il calore specifico del piombo vale 130 J/kg∙K.
Quanto vale la temperatura di equilibrio raggiunta dal sistema, trascurando il calore che viene ceduto dal piombo al calorimetro?
Dai dati forniti dal problema notiamo che anche in questo caso, il metallo presenta una temperatura superiore a quella dell’acqua in cui viene immerso; di conseguenza, sarà il metallo a cedere calore all’acqua, presentando un valore negativo per la sua quantità di calore scambiato.
Il calore acquistato dall’acqua, invece, avrà segno positivo.
Possiamo procedere applicando la formula vista in precedenza per risalire direttamente al valore della temperatura di equilibrio.
$ T_e = frac( c_a * m_a * T_a + c_m * m_m * T_m)(c_a * m_a + c_m * m_m)$
Prima di procedere con i calcoli, però, trasformiamo le grandezze nelle giuste unità di misura:
$ T_a = 15°C = 288 K$
$T_p = 90°C = 363 K $
Ricordiamo che il calore specifico dell’acqua, anche se non viene fornito tra i dati del problema, è un valore noto; esso corrisponde, infatti, alla quantità di energia necessaria per far aumentare di 1K una massa d’acqua di 1Kg, che sappiamo essere 4186J.
Possiamo procedere sostituendo i valori numerici alla formula precedente:
$ T_e = frac( 4186 * 0,5 * 288 + 130 * 0,3 * 363)(4186 * 0,5 + 130 * 0,3) = 289,37 K = 16,22° C$
Potrebbero interessarti
Appunti: Il calore
Appunti: Il potere calorifico
