Il lavoro termodinamico - Matematicamente

Quando un sistema subisce una trasformazione quasistatica, viene compiuto un lavoro. Ad esempio, se consideriamo un gas racchiuso all’interno di un recipiente dotato di pistone; se scaldiamo il sistema, vi sarà un aumento del volume del sistema, e un conseguente innalzamento del pistone.

In questo caso, il sistema sta compiendo un lavoro positivo.

Se, invece, comprimiamo il pistone, facendo diminuire il volume del gas, siamo noi che compiamo un lavoro positivo; il lavoro compiuto dal gas, invece, avrà segno negativo.

In generale, possiamo esprimere il valore del lavoro che viene compiuto come prodotto della pressione del gas per la variazione di volume che esso subisce:

$ W = p * ∆V $

Questa formula spiega, quindi, il segno del lavoro; nel caso in cui il gas si espande, il volume finale è maggiore di quello iniziale, quindi il lavoro ha segno positivo. Nel caso in cui, invece, il gas viene compresso, il volume finale è minore di quello iniziale, quindi il lavoro compiuto dal gas è negativo.

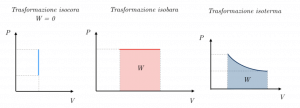
In generale, se osserviamo un grafico pressione-volume, possiamo da questo ricavare il valore del lavoro compiuto dal gas durante la trasformazione. Il modulo del lavoro, infatti, è dato dall’area della regione compresa tra la curva e l’asse orizzontale; esso è quindi dato dall’integrale della funzione che rappresenta la curva.

Notiamo, quindi, che nel caso delle trasformazioni isocore, in cui si ha ∆V = 0, effettivamente non è possibile calcolare tale area, che risulterà quindi pari a zero.

lavoro-trasformazioni — Lavoro e trasformazioni quasistatiche

Vediamo ora il caso di una trasformazione ciclica, cioè una trasformazione per cui li stato iniziale del sistema corrisponde allo stato finale.

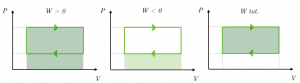
Durante la trasformazione, il sistema subisce sia una fase di compressione, sia una fase di espansione; a queste due fasi corrispondono, rispettivamente, un lavoro negativo e un lavoro positivo; calcolando la loro somma otterremo il lavoro complessivo.

Rappresentando la situazione in un grafico pressione-volume notiamo che il lavoro finale è dato dall’area della regione racchiusa all’interno del grafico; questa è ottenuta come differenza delle aree della parte superiore (cioè della espansione) e della parte inferiore (cioè della compressione) del grafico.

Il lavoro, a differenza dell’energia interna, non è una finzione di stato; di conseguenza non dipende esclusivamente dallo stato iniziale e da quello finale della trasformazione, ma dipende proprio dal tipo di trasformazione.

Dal momento che il lavoro è dato proprio dall’area sottesa dalla curva della trasformazione, a parità di punto iniziale e di punto finale, due trasformazioni che presentano curve differenti avranno anche valori differenti delle aree che esse sottendono.

Esercizio

Consideriamo un gas perfetto contenuto in un recipiente dotato di pistone mobile. Il gas si espande compiendo un lavoro positivo pari a 4500 J. Sapendo che la trasformazione è isobara, e il valore della pressione è di $2,5 * 10^5 Pa$, e che il gas raggiunge un volume finale di $45 dm^3$, quale era il volume iniziale del gas?

Come abbiamo visto in precedenza, il lavoro compiuto dal gas durante una trasformazione è dato dal prodotto della pressione del gas per la variazione di volume (volume finale meno volume iniziale).

$W = p * ∆V = p * (V_f – V_i)$

Da questa relazione, quindi, possiamo ricavare la formula inversa per il valore del volume iniziale:

$V_i = frac(-W + p * V_f)(p) = – fracW/p + V_f $

Ricordiamo che il valore del volume deve essere espresso in metri cubi, quindi occorre trasformare il valore del volume finale:

$ 45 dm^3 = 45 * 10^(-3) m^3 = 0,045 m^3$

Sostituiamo i valori numerici e calcoliamo il valore del volume occupato inizialmente dal gas:

$V_i = – fracW/p + V_f = – frac(4500)(2,5 * 10^5) + 45 = 0,027 m^3 = 27 dm^3$